Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Dos móviles sobre el eje OX acercándose II (Ex.Oct/17)

De Laplace

Contenido

1 Enunciado

Un móvil A recorre el eje OX con una aceleración constante 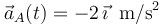\vec{a}_{A}(t)=-2\,\vec{\imath} \,\,\,\mathrm{m}/\mathrm{s}^2\,, hallándose en reposo en el punto 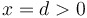x=d>0\, en el instante inicial 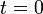t=0\,. En ese mismo instante un segundo móvil B, que se encuentra en reposo en el punto 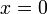x=0\,, comienza a moverse con una aceleración creciente en el tiempo según la fórmula:

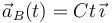
\vec{a}_B(t)=C t\,\vec{\imath}\,

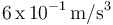donde C\, es una constante de valor igual a 6\,\mathrm{x}\,10^{-1}\,\mathrm{m}/\mathrm{s}^{3}\,.

  1. ¿Qué distancia separaba inicialmente a los móviles si se cruzan justo en el punto medio entre sus posiciones de partida?
  2. ¿Qué celeridad tiene el móvil B en el instante en que ambos se cruzan?

2 Posiciones y velocidades en función del tiempo

Comenzaremos estudiando la cinemática del móvil B.

Conforme a las definiciones de velocidad instantánea y aceleración instantánea, podemos escribir:

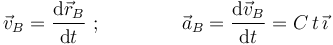
\vec{v}_B=\frac{\mathrm{d}\vec{r}_B}{\mathrm{d}t}\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}_B=\frac{\mathrm{d}\vec{v}_B}{\mathrm{d}t}=C\, t\,\vec{\imath}

Conocemos también las condiciones iniciales de posición y velocidad:

\vec{r}_B(0)=\vec{0}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}_B(0)=\vec{0}

Por tanto, determinar la velocidad y la posición del móvil B en función del tiempo se reduce a integrar su aceleración una y dos veces, respectivamente, entre el instante inicial y el instante genérico t\,:

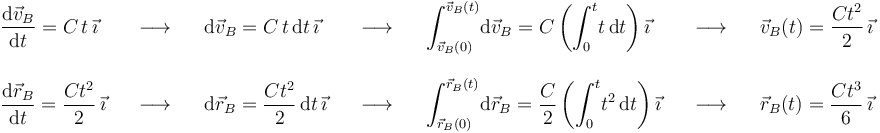
\begin{array}{lllllll}\displaystyle\frac{\mathrm{d}\vec{v}_B}{\mathrm{d}t}=C\, t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \mathrm{d}\vec{v}_B=C\, t\,\mathrm{d}t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{v}_B(0)}^{\vec{v}_B(t)}\!\mathrm{d}\vec{v}_B=C\left(\displaystyle\int_{0}^{t}\!t\,\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}_B(t)=\displaystyle\frac{Ct^2}{2}\,\vec{\imath} \\ \\ \displaystyle\frac{\mathrm{d}\vec{r}_B}{\mathrm{d}t}=\frac{Ct^2}{2}\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \mathrm{d}\vec{r}_B=\displaystyle\frac{Ct^2}{2}\,\mathrm{d}t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{r}_B(0)}^{\vec{r}_B(t)}\!\mathrm{d}\vec{r}_B=\frac{C}{2}\left(\displaystyle\int_{0}^{t}\!t^2\,\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{r}_B(t)=\displaystyle\frac{Ct^3}{6}\,\vec{\imath}\end{array}

La cinemática del móvil A es algo más sencilla, dado que realiza un movimiento rectilíneo uniformemente acelerado. No obstante, razonaremos de forma análoga a como lo hemos hecho para el móvil B, es decir, obviaremos que conocemos de memoria las fórmulas para la posición y velocidad en un movimiento rectilíneo uniformemente acelerado.

Conforme a las definiciones de velocidad instantánea y aceleración instantánea, podemos escribir:

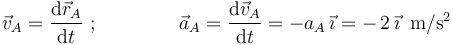
\vec{v}_A=\frac{\mathrm{d}\vec{r}_A}{\mathrm{d}t}\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}_A=\frac{\mathrm{d}\vec{v}_A}{\mathrm{d}t}=-a_A\,\vec{\imath}=-\,2\,\vec{\imath}\,\,\,\mathrm{m}/\mathrm{s}^2

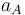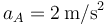donde hemos llamado a_A\, al módulo de la aceleración constante del móvil A (cuyo valor es a_A=2\,\mathrm{m}/\mathrm{s}^2\,).

Conocemos también las condiciones iniciales de posición y velocidad:

\vec{r}_A(0)=d\,\vec{\imath}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}_A(0)=\vec{0}

Por tanto, determinar la velocidad y la posición del móvil A en función del tiempo se reduce a integrar su aceleración una y dos veces, respectivamente, entre el instante inicial y el instante genérico t\,:

\begin{array}{lllllll}\displaystyle\frac{\mathrm{d}\vec{v}_A}{\mathrm{d}t}=-a_A\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \mathrm{d}\vec{v}_A=-a_A\,\mathrm{d}t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{v}_A(0)}^{\vec{v}_A(t)}\!\mathrm{d}\vec{v}_A=-a_A\left(\displaystyle\int_{0}^{t}\!\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}_A(t)=-a_A t\,\vec{\imath} \\ \\ \displaystyle\frac{\mathrm{d}\vec{r}_A}{\mathrm{d}t}=-a_A t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \mathrm{d}\vec{r}_A=\displaystyle-a_A t\,\mathrm{d}t\,\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \displaystyle\int_{\vec{r}_A(0)}^{\vec{r}_A(t)}\!\mathrm{d}\vec{r}_A=-a_A\left(\displaystyle\int_{0}^{t}\!t\,\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{r}_A(t)=\left[d-\displaystyle\frac{a_At^2}{2}\right]\,\vec{\imath}\end{array}

3 Distancia inicial entre ambos móviles sabiendo que se cruzan en el punto medio

Conocidas las posiciones de A y B en función del tiempo:

\vec{r}_A(t)=\left[d-\displaystyle\frac{a_At^2}{2}\right]\,\vec{\imath}\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{r}_B(t)=\displaystyle\frac{Ct^3}{6}\,\vec{\imath}

se exige que en cierto instante (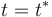\,t=t^*\,) ambos móviles se hallen simultáneamente en el punto medio entre sus posiciones de partida (\,x=d/2\,):

\left\{\begin{array}{l} d-\displaystyle\frac{a_A(t^*)^2}{2}=\frac{d}{2} \\ \\ \displaystyle\frac{C(t^*)^3}{6}=\frac{d}{2}\end{array} \right.

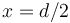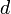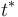y resolviendo este sistema de dos ecuaciones para las incógnitas d\, y t^*\,, se obtiene:

t^*=\displaystyle\frac{3\,a_A}{C}\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, d=\displaystyle\frac{9\,a_A^3}{C^2}

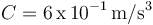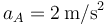y sustituyendo los datos numéricos (C=6\,\mathrm{x}\,10^{-1}\,\mathrm{m}/\mathrm{s}^{3}\,, a_A=2\,\mathrm{m}/\mathrm{s}^2\,):

t^*=\frac{3\,\mathrm{x}\,2\,\mathrm{m}/\mathrm{s}^2}{6\,\mathrm{x}\,10^{-1}\,\mathrm{m}/\mathrm{s}^{3}}=10\,\mathrm{s}\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, d=\displaystyle\frac{9\,\mathrm{x}\,8\,\mathrm{m}^3/\mathrm{s}^6}{36\,\mathrm{x}\,10^{-2}\,\mathrm{m}^2/\mathrm{s}^{6}}=200\,\mathrm{m}

Así que la distancia que separaba inicialmente a los dos móviles es 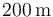200\,\mathrm{m}\,.

4 Celeridad del móvil B en el instante de cruce

Conocida la velocidad de B en función del tiempo:

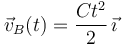
\vec{v}_B(t)=\displaystyle\frac{Ct^2}{2}\,\vec{\imath}

es fácil evaluar su celeridad en el instante de cruce 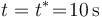\,t=t^*\!=\!10\,\mathrm{s}\,:

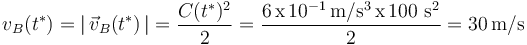
v_B(t^*)=|\,\vec{v}_B(t^*)\,|=\displaystyle\frac{C(t^*)^2}{2}=\displaystyle\frac{6\,\mathrm{x}\,10^{-1}\,\mathrm{m}/\mathrm{s}^3\,\mathrm{x}\,100\,\,\mathrm{s}^2}{2}=30\,\mathrm{m}/\mathrm{s}

Así que la celeridad que tiene el móvil B en el instante en que ambos se cruzan es 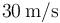30\,\mathrm{m}/\mathrm{s}\,.

Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Dos_m%C3%B3viles_sobre_el_eje_OX_acerc%C3%A1ndose_II_(Ex.Oct/17)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:32, 22 feb 2018. - Esta página ha sido visitada 2.121 veces. - Aviso legal - Acerca de Laplace