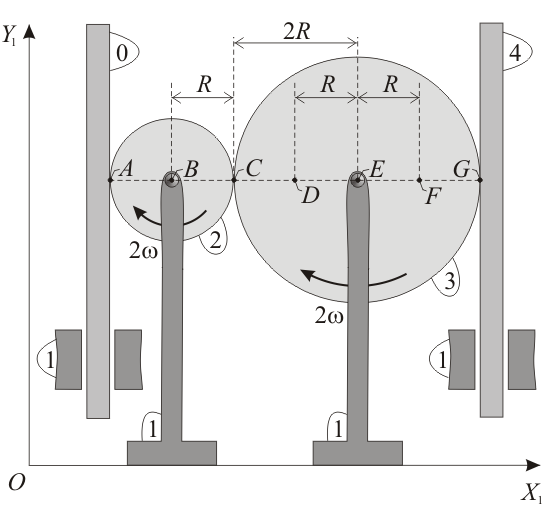
No Boletín - Dos discos y dos barras (Ex.Ene/19)
De Laplace
Contenido |
1 Enunciado
El sistema mecánico de la figura está constituido por cuatro sólidos móviles (las barras "0" y "4", y los discos "2" y "3"), los cuales se mantienen siempre contenidos en el plano fijo  (sólido "1"). El disco "2", de radio
(sólido "1"). El disco "2", de radio  , rota con velocidad angular constante
, rota con velocidad angular constante 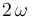 (en el sentido indicado en la figura) alrededor de su centro fijo
(en el sentido indicado en la figura) alrededor de su centro fijo  . El disco "3", de radio
. El disco "3", de radio  , rota con velocidad angular constante
, rota con velocidad angular constante 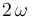 (en el sentido indicado en la figura) alrededor de su centro fijo
(en el sentido indicado en la figura) alrededor de su centro fijo  . Las barras "0" y "4", de longitudes indefinidas, experimentan sendas traslaciones verticales respecto al plano fijo
. Las barras "0" y "4", de longitudes indefinidas, experimentan sendas traslaciones verticales respecto al plano fijo  al ser arrastradas respectivamente por las rotaciones de los discos con los que mantienen contacto permanente, ya que el disco "2" rueda sin deslizar sobre la barra "0", y el disco "3" rueda sin deslizar sobre la barra "4".
al ser arrastradas respectivamente por las rotaciones de los discos con los que mantienen contacto permanente, ya que el disco "2" rueda sin deslizar sobre la barra "0", y el disco "3" rueda sin deslizar sobre la barra "4".
- ¿Con qué velocidades se trasladan las barras?
- ¿Cómo se clasifica el movimiento
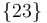 ?
?
- ¿Dónde está el centro instantáneo de rotación
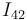 ?
?
- ¿Cuánto vale la aceleración del punto
 de contacto entre ambos discos en el movimiento
de contacto entre ambos discos en el movimiento 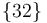 ?
?
2 Velocidades de traslación de las barras
Los movimientos absolutos de los discos (movimientos  y
y 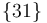 ) se describen en el enunciado como sendas rotaciones alrededor de centros fijos, deduciéndose trivialmente que sus reducciones cinemáticas son:
) se describen en el enunciado como sendas rotaciones alrededor de centros fijos, deduciéndose trivialmente que sus reducciones cinemáticas son:
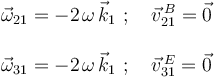
Se nos dice que el disco "2" rueda sin deslizar sobre la barra "0". Esta ausencia de deslizamiento en el movimiento relativo  conlleva que el punto de contacto entre ambos sólidos (punto
conlleva que el punto de contacto entre ambos sólidos (punto  ) tiene velocidad relativa
) tiene velocidad relativa  nula:
nula:
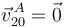
También se nos dice que el disco "3" rueda sin deslizar sobre la barra "4". Esta ausencia de deslizamiento en el movimiento relativo  conlleva que el punto de contacto entre ambos sólidos (punto
conlleva que el punto de contacto entre ambos sólidos (punto  ) tiene velocidad relativa
) tiene velocidad relativa 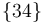 nula:
nula:

Entonces, aplicando la ley de composición de velocidades en dichos puntos de contacto, se obtiene que:
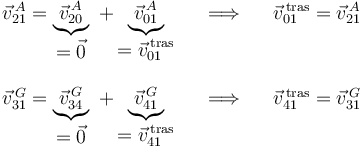
donde se ha tenido en cuenta que los campos de velocidades de los movimientos absolutos de las barras (movimientos  y
y 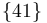 ) son uniformes (se trata de sendas traslaciones verticales según nos indica el enunciado).
) son uniformes (se trata de sendas traslaciones verticales según nos indica el enunciado).
Por tanto, las velocidades de traslación de ambas barras se pueden determinar fácilmente a partir de las igualdades deducidas y aplicando las ecuaciones de los campos de velocidades  y
y 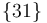 , respectivamente:
, respectivamente:
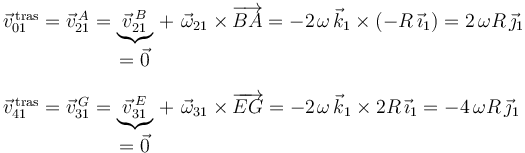
3 Clasificación del movimiento {23}
Aplicando la ley de composición de velocidades angulares, se deduce la nulidad de 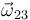 :
:
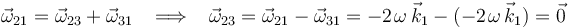
Por tanto, el campo de velocidades  es uniforme. Calculamos ahora el valor de dicho campo determinando la velocidad
es uniforme. Calculamos ahora el valor de dicho campo determinando la velocidad 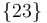 de un punto cualquiera, por ejemplo, del punto
de un punto cualquiera, por ejemplo, del punto 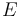 (utilizamos para ello la ley de composición de velocidades y la ecuación del campo de velocidades
(utilizamos para ello la ley de composición de velocidades y la ecuación del campo de velocidades  ):
):
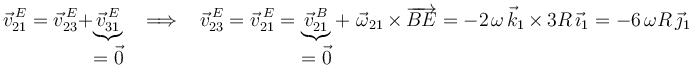
Una vez comprobado que el campo de velocidades 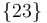 es uniforme y no nulo, podemos clasificar el movimiento
es uniforme y no nulo, podemos clasificar el movimiento 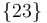 como una TRASLACIÓN de velocidad
como una TRASLACIÓN de velocidad 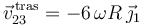 .
.
4 Centro instantáneo de rotación del movimiento {42}
Determinaremos la posición del centro instantáneo de rotación 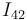 aplicando el procedimiento analítico, es decir, calcularemos la reducción cinemática del movimiento
aplicando el procedimiento analítico, es decir, calcularemos la reducción cinemática del movimiento 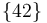 en algún punto (por ejemplo, el punto
en algún punto (por ejemplo, el punto  ) y después utilizaremos la fórmula deducida en la teoría para determinar la posición de
) y después utilizaremos la fórmula deducida en la teoría para determinar la posición de 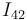 respecto a dicho punto.
respecto a dicho punto.
Así pues, calculamos en primer lugar la reducción cinemática del movimiento 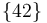 en el punto
en el punto  (aplicando para ello la ley de composición de velocidades angulares y la ley de composición de velocidades):
(aplicando para ello la ley de composición de velocidades angulares y la ley de composición de velocidades):

donde se ha tenido en cuenta que la velocidad angular 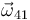 es nula por ser el movimiento
es nula por ser el movimiento 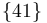 una traslación.
una traslación.
Y a continuación aplicamos la fórmula que nos da la posición de 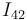 respecto al punto
respecto al punto  :
:
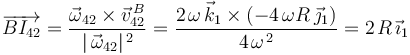
Por tanto, a la vista de este resultado y tras inspeccionar la figura del enunciado, llegamos a la conclusión de que el centro instantáneo de rotación del movimiento 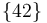 coincide con el punto
coincide con el punto  :
:
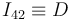
5 Aceleración {32} del punto C de contacto entre ambos discos
Aplicando la ley de composición de aceleraciones en el punto  y despejando
y despejando 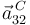 , se obtiene:
, se obtiene:

A continuación, calculamos los tres términos que necesitamos para determinar 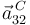 :
:
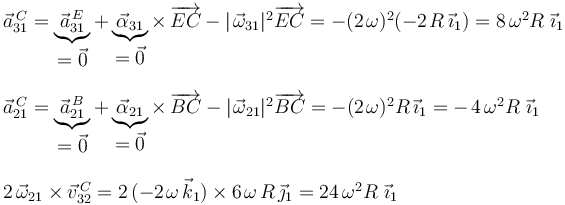
donde se ha tenido presente que 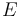 es un punto fijo en el movimiento
es un punto fijo en el movimiento 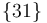 (por eso
(por eso 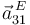 es nula), que
es nula), que  es un punto fijo en el movimiento
es un punto fijo en el movimiento  (por eso
(por eso 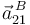 es nula), que las velocidades angulares
es nula), que las velocidades angulares  y
y 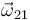 son constantes (por eso
son constantes (por eso 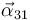 y
y 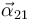 son nulas), y que las velocidades recíprocas son opuestas (por eso
son nulas), y que las velocidades recíprocas son opuestas (por eso 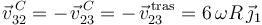 ).
).
Sustituyendo el valor de los tres términos en la expresión de 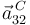 deducida arriba, se obtiene:
deducida arriba, se obtiene:
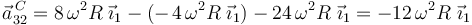
6 Procedimiento alternativo para determinar la aceleración {32} del punto C
Según se comprobó anteriormente, el movimiento 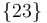 es una traslación permanente de velocidad
es una traslación permanente de velocidad 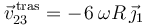 . Por consiguiente, su movimiento recíproco
. Por consiguiente, su movimiento recíproco 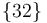 es otra traslación permanente de velocidad
es otra traslación permanente de velocidad 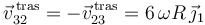 .
.
Ahora bien, el campo de aceleraciones de una traslación permanente es uniforme (esto se debe a que el campo de velocidades de una traslación permanente es uniforme en todo instante). Así que llegamos a la conclusión de que todos los puntos tienen la misma aceleración en el movimiento 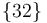 , y además esta aceleración puede calcularse a partir de su propia definición, es decir, derivando respecto al tiempo la velocidad de traslación del movimiento
, y además esta aceleración puede calcularse a partir de su propia definición, es decir, derivando respecto al tiempo la velocidad de traslación del movimiento 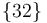 :
:
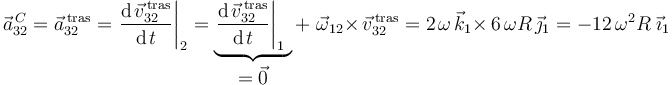
donde se ha aplicado la fórmula de Poisson para la derivación, y se ha tenido en cuenta que las velocidades angulares recíprocas son opuestas (por eso  ).
).