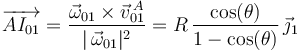No Boletín - Disco y varilla guiada (Ex.Ene/15)
De Laplace
Contenido |
1 Enunciado
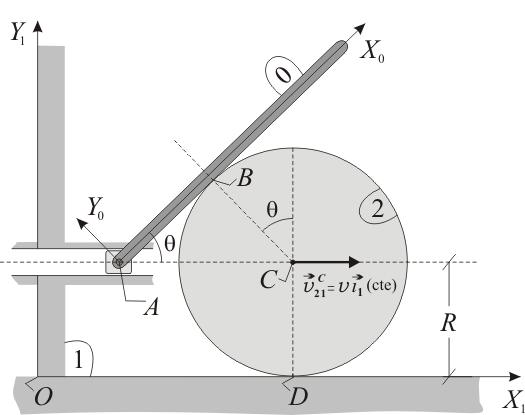
El mecanismo de la figura está formado por un disco rígido (sólido "2") de radio  , que rueda sin deslizar (punto
, que rueda sin deslizar (punto  ) sobre el eje horizontal
) sobre el eje horizontal 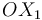 de la escuadra fija
de la escuadra fija  (sólido "1"), y cuyo centro
(sólido "1"), y cuyo centro  avanza con velocidad constante
avanza con velocidad constante 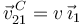 ; y por una varilla rígida (sólido "0") de grosor despreciable y longitud indefinida, la cual rueda sin deslizar (punto
; y por una varilla rígida (sólido "0") de grosor despreciable y longitud indefinida, la cual rueda sin deslizar (punto  ) sobre el citado disco, mientras que su
extremo
) sobre el citado disco, mientras que su
extremo  está obligado a recorrer una guía horizontal fija de ecuación
está obligado a recorrer una guía horizontal fija de ecuación 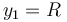 .
.
Como parámetro auxiliar descriptivo de la posición del mecanismo, se define el ángulo  de la figura. Se pide:
de la figura. Se pide:
- Determinación gráfica (razonada) de las posiciones de los centros instantáneos de rotación
 ,
, 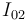 e
e 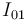 .
.
- Reducción cinemática del movimiento
 en el punto
en el punto  , es decir,
, es decir, 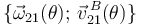 .
.
- Reducción cinemática del movimiento
 en el punto
en el punto  , es decir,
, es decir, 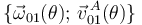 .
.
- Determinación analítica de la posición del centro instantáneo de rotación
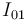 , es decir,
, es decir,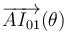 .
.
Aviso: Las magnitudes pedidas deben quedar expresadas en función de  ,
,  y/o
y/o  , pero NO en función de
, pero NO en función de 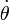 .
.
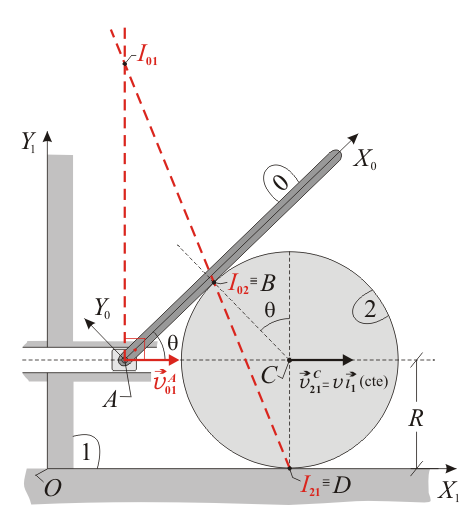
2 Determinación gráfica de los tres centros instantáneos de rotación
Sabemos que el disco (sólido "2") rueda sin deslizar sobre el eje horizontal 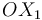 de la escuadra fija
de la escuadra fija  (sólido "1"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento
(sólido "1"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento  coincide con el punto de contacto disco-eje (punto
coincide con el punto de contacto disco-eje (punto  ):
):
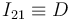
También sabemos que la varilla (sólido "0") rueda sin deslizar sobre el disco (sólido "2"). Esta otra ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento 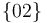 coincide con el punto de contacto varilla-disco (punto
coincide con el punto de contacto varilla-disco (punto  ):
):

En cuanto al movimiento  , se nos indica que el extremo
, se nos indica que el extremo  de la varilla está obligado a recorrer una guía horizontal fija (paralela al eje
de la varilla está obligado a recorrer una guía horizontal fija (paralela al eje 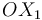 ), lo cual nos permite saber que la dirección de la velocidad
), lo cual nos permite saber que la dirección de la velocidad 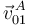 es necesariamente horizontal. Trazando la perpendicular a dicha velocidad en el punto
es necesariamente horizontal. Trazando la perpendicular a dicha velocidad en el punto  y trazando la recta que pasa por los puntos
y trazando la recta que pasa por los puntos 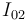 e
e  (en aplicación del teorema de los tres centros), hallaremos el punto
(en aplicación del teorema de los tres centros), hallaremos el punto 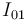 en la intersección de ambas rectas:
en la intersección de ambas rectas:
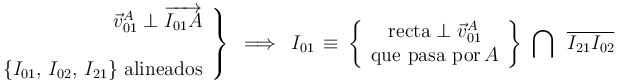
3 Reducción cinemática (en B) del movimiento {21}
El vector velocidad angular
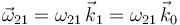 (de dirección perpendicular al plano director
(de dirección perpendicular al plano director  ) se determina relacionando, mediante la ecuación del campo de velocidades del movimiento
) se determina relacionando, mediante la ecuación del campo de velocidades del movimiento  , las velocidades (conocidas) del punto
, las velocidades (conocidas) del punto  y del punto
y del punto 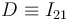 :
:
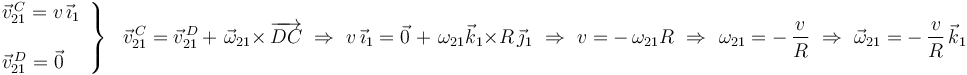
Y utilizando de nuevo la ecuación del campo de velocidades del movimiento  , obtenemos la velocidad
, obtenemos la velocidad 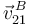 a partir de la velocidad
a partir de la velocidad 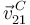 (también podría calcularse a partir de
(también podría calcularse a partir de 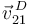 ):
):
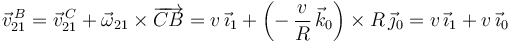
Finalmente, sustituyendo 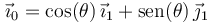 en la expresión obtenida para
en la expresión obtenida para 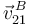 , se llega a:
, se llega a:
![\vec{v}^{\, B}_{21}=v\left[1+\mathrm{cos}(\theta)\right]\,\vec{\imath}_1+
v\,\mathrm{sen}(\theta)\,\vec{\jmath}_1](/wiki/images/math/4/4/b/44baa5a6e24f2cd86ba4f4f0abd4851e.png)
4 Reducción cinemática (en A) del movimiento {01}
Una vez conocida 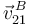 , y teniendo en cuenta que
, y teniendo en cuenta que 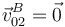 (ya que
(ya que 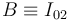 ), la ley de composición de velocidades permite determinar la velocidad
), la ley de composición de velocidades permite determinar la velocidad 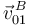 :
:
![\vec{v}^{\, B}_{01}=\vec{v}^{\, B}_{02}+\vec{v}^{\, B}_{21}=\vec{0}+\vec{v}^{\, B}_{21}=
v\left[1+\mathrm{cos}(\theta)\right]\,\vec{\imath}_1+v\,\mathrm{sen}(\theta)\,\vec{\jmath}_1](/wiki/images/math/b/6/4/b6401a9f2fc521a8bb735c8f981d9689.png)
Por otra parte, y tal como se explicó en el primer apartado, sabemos a priori que la dirección de la velocidad 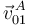 es necesariamente horizontal, es decir,
es necesariamente horizontal, es decir, 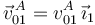 .
.
Entonces, los vectores 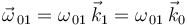 (de dirección perpendicular al plano director
(de dirección perpendicular al plano director  ) y
) y 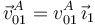 se podrán determinar exigiendo el cumplimiento de la ecuación del campo de velocidades del movimiento
se podrán determinar exigiendo el cumplimiento de la ecuación del campo de velocidades del movimiento  para los puntos
para los puntos  y
y  :
:

Pero antes debemos calcular el último término de esta ecuación:
![\vec{\omega}_{01}\times \overrightarrow{AB}=\omega_{01}\vec{k}_0\times
R\,\mathrm{cotg}(\theta)\,\vec{\imath}_0=\omega_{01}R\,\mathrm{cotg}(\theta)\,\vec{\jmath}_0=
\omega_{01}R\left[-\mathrm{cos}(\theta)\,\vec{\imath}_1+
\displaystyle\frac{\mathrm{cos}^2(\theta)}{\mathrm{sen}(\theta)}\,\vec{\jmath}_1\right]](/wiki/images/math/c/e/4/ce4c5a94935f94581f234cb889dde1f7.png)
donde la expresión del vector 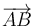 en función de
en función de  se ha deducido por simple inspección de las razones trigonométricas en el triángulo rectángulo
se ha deducido por simple inspección de las razones trigonométricas en el triángulo rectángulo 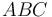 , y donde además se ha tenido en cuenta que
, y donde además se ha tenido en cuenta que
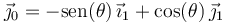 .
.
Volviendo a la ecuación del campo de velocidades del movimiento  , e igualando componente a componente los dos
miembros de dicha ecuación vectorial, se obtiene el siguiente sistema de dos ecuaciones para las dos incógnitas
, e igualando componente a componente los dos
miembros de dicha ecuación vectorial, se obtiene el siguiente sistema de dos ecuaciones para las dos incógnitas 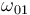 y
y 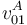 :
:
![\vec{v}^{\, B}_{01}=\vec{v}^{\, A}_{01}+\,\vec{\omega}_{01}\times \overrightarrow{AB}\,\,\longrightarrow\,\,
\left\{\begin{array}{l} v\left[1+\mathrm{cos}(\theta)\right]=v^{A}_{01}-\omega_{01}R\,\mathrm{cos}(\theta)
\\ \\ v\,\mathrm{sen}(\theta)=\omega_{01}R\,\displaystyle\frac{\mathrm{cos}^2(\theta)}{\mathrm{sen}(\theta)}
\end{array}\right.](/wiki/images/math/9/3/6/936f022d431ba4f62dd18e508e13c8c0.png)
Resolviendo este sistema de ecuaciones, y sustituyendo el valor de las incógnitas en las correspondientes expresiones vectoriales, se obtiene:
![\vec{\omega}_{01}=\displaystyle\frac{v}{R}\,
\mathrm{tg}^2(\theta)\,\vec{k}_{1} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\vec{v}^{\, A}_{01}=v\left[1+\displaystyle\frac{1}{\mathrm{cos}(\theta)}\right]\vec{\imath}_{1}](/wiki/images/math/3/3/a/33a8c6ea2d5d04d0aa9048c81af12c4f.png)
5 Determinación analítica del C.I.R.{01}
La posición del centro instantáneo de rotación 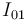 respecto al punto
respecto al punto  se determina mediante la fórmula:
se determina mediante la fórmula: