No Boletín - Disco rueda sin deslizar sobre triángulo (Ex.Feb/17)

De Laplace

1 Enunciado

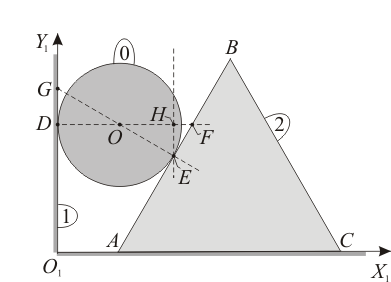
El sistema mecánico de la figura, contenido en todo instante en el plano fijo 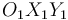$O_1X_1Y_1\,$ (sólido "1"), está constituido por un triángulo 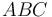$ABC\,$ (sólido "2") que desliza sobre el eje 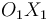$O_1X_1\,$ , manteniendo su lado 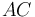$AC\,$ completo en contacto con dicho eje; y por un disco (sólido "0"), de centro $O\,$ , que rueda sin deslizar sobre el lado 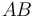$AB\,$ del triángulo, y a la vez rueda y desliza sobre el eje $O_1Y_1\,$ .

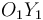¿Dónde se halla el centro instantáneo de rotación 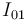$I_{01}\,$ ?

$\mathrm{(a)}\,\,\,I_{01}\equiv G\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(b)}\,\,\,I_{01}\equiv F\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(c)}\,\,\,I_{01}\equiv H\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(d)}\,\,\,I_{01}\equiv D$

2 Solución

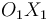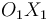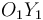Que el triángulo "2" deslice sobre el eje $O_1X_1\,$ de la escuadra fija "1", manteniendo siempre su base completamente en contacto con dicho eje, implica que el movimiento $\{21\}\,$ es una traslación paralela al eje $O_1X_1\,$ . En consecuencia, el centro instantáneo de rotación del movimiento $\{21\}\,$ se halla en el infinito en la dirección paralela al eje $O_1Y_1\,$ (perpendicular a la dirección de traslación):

$I_{21}\rightarrow\infty\parallel O_1Y_1\perp \vec{v}^{\,\mathrm{tras}}_{21}$

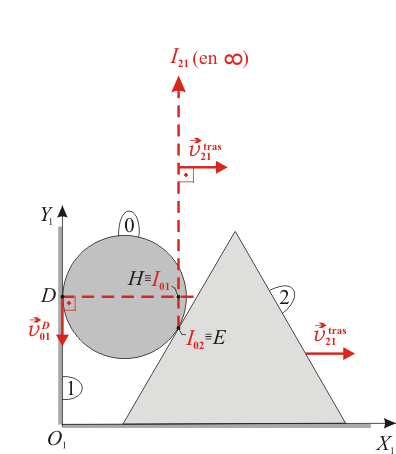
Por otra parte, el disco "0" rueda sin deslizar sobre el triángulo "2". Esta ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento 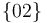$\{02\}\,$ coincide con el punto de contacto disco-triángulo:

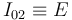
$I_{02}\equiv E$

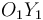En cuanto al movimiento $\{01\}\,$ , al ser $D\,$ el punto de contacto entre el disco "0" y el eje $O_1Y_1\,$ de la escuadra fija "1", sabemos que la velocidad 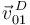$\vec{v}^{\, D}_{01}\,$ es la velocidad de deslizamiento entre ambos sólidos y, por tanto, ha de ser tangencial al contacto (si no fuera así, los sólidos dejarían de estar en contacto):

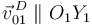
$\vec{v}^{\, D}_{01}\parallel O_1Y_1$

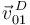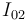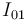Entonces, trazando la perpendicular a $\vec{v}^{\, D}_{01}\,$ en el punto $D\,$ y trazando la recta que pasa por los puntos $I_{02}\,$ e $I_{21}\,$ (en aplicación del teorema de los tres centros), hallaremos el punto $I_{01}\,$ en la intersección de ambas rectas:

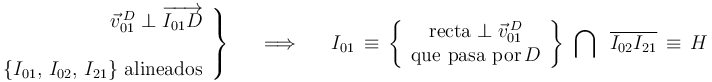
$\left.\begin{array}{r} \vec{v}_{01}^{\, D}\perp\overrightarrow{I_{01}D} \\ \\ \{I_{01},\, I_{02},\,I_{21} \} \,\,\mathrm{alineados} \end{array}\right\} \,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\, I_{01}\,\equiv\,\left\{\begin{array}{c} \mathrm{recta}\perp\vec{v}_{01}^{\, D} \\ \mathrm{que}\,\,\mathrm{pasa}\,\,\mathrm{por} \, D \end{array}\right\}\,\,\bigcap\,\,\,\overline{I_{02}I_{21}}\,\equiv\,H$

Así que la respuesta correcta a la pregunta planteada es la opción (c) 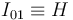$\,\,\,I_{01}\equiv H\,$ .

No Boletín - Disco rueda sin deslizar sobre triángulo (Ex.Feb/17)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES