No Boletín - Disco rodando sobre escuadra giratoria (Ex.Ene/12)
De Laplace
Contenido |
1 Enunciado
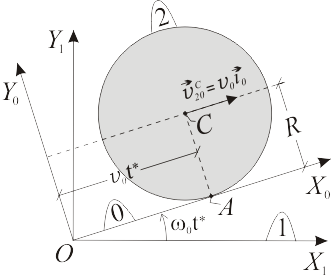
Un disco de radio  (sólido "2"), contenido en el plano
(sólido "2"), contenido en el plano 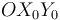 , rueda sin deslizar sobre el eje
, rueda sin deslizar sobre el eje 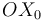 (sólido "0"), de tal modo que su centro
(sólido "0"), de tal modo que su centro  avanza con velocidad relativa constante
avanza con velocidad relativa constante 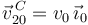 . Al mismo tiempo, la escuadra
. Al mismo tiempo, la escuadra 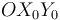 (sólido "0"), articulada en su punto
(sólido "0"), articulada en su punto  al origen de coordenadas de la escuadra fija y coplanaria
al origen de coordenadas de la escuadra fija y coplanaria  (sólido "1"), rota con velocidad angular absoluta constante
(sólido "1"), rota con velocidad angular absoluta constante 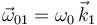 alrededor del eje fijo
alrededor del eje fijo 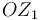 . La posición del sistema que se representa en la figura, y a la cual se refieren las siguientes preguntas, corresponde al instante
. La posición del sistema que se representa en la figura, y a la cual se refieren las siguientes preguntas, corresponde al instante 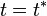 .
.
- ¿Dónde se halla el centro instantáneo de rotación
 ?
?
- Determine la aceleración instantánea
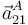 (ver
(ver  en figura).
en figura).
- ¿En qué caso particular el movimiento {21} es una traslación?
2 C.I.R.{21}: localización aproximada mediante el teorema de los tres centros
Se nos indica que el disco (sólido "2") rueda sin deslizar sobre el eje 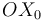 (sólido "0"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {20} coincide con el punto de contacto disco-eje:
(sólido "0"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {20} coincide con el punto de contacto disco-eje:
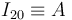
La escuadra 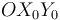 (sólido "0") está articulada en su punto
(sólido "0") está articulada en su punto  al origen de coordenadas de la escuadra fija y coplanaria
al origen de coordenadas de la escuadra fija y coplanaria  (sólido "1"). Por tanto, dicho punto
(sólido "1"). Por tanto, dicho punto  es un punto fijo (centro permanente de rotación) en el movimiento {01}:
es un punto fijo (centro permanente de rotación) en el movimiento {01}:
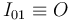
Entonces, aplicando el teorema de los tres centros, podemos asegurar que el centro instantáneo de rotación del movimiento {21} ha de estar en la recta que pasa por los puntos  y
y  , es decir, ha de estar en el eje
, es decir, ha de estar en el eje 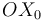 .
.
NOTA: Este problema se planteó en examen como ejercicio tipo test, y la respuesta correcta al presente apartado era la que afirmaba que el C.I.R.{21} se halla en el eje 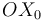 . No obstante, completaremos a continuación esta solución determinando la localización exacta del C.I.R.{21}. Para ello, necesitamos calcular previamente la reducción cinemática del movimiento {21} en algún punto, por ejemplo en el punto
. No obstante, completaremos a continuación esta solución determinando la localización exacta del C.I.R.{21}. Para ello, necesitamos calcular previamente la reducción cinemática del movimiento {21} en algún punto, por ejemplo en el punto  . Pero la reducción cinemática de {21} en
. Pero la reducción cinemática de {21} en  se puede determinar fácilmente mediante las leyes de composición si antes hallamos las reducciones cinemáticas de {01} y {20} en dicho punto.
se puede determinar fácilmente mediante las leyes de composición si antes hallamos las reducciones cinemáticas de {01} y {20} en dicho punto.
3 C.I.R.{21}: localización exacta mediante determinación analítica
La reducción cinemática de {01} en  ya se conoce:
ya se conoce:
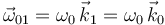 ;
; 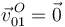
Hallemos ahora la reducción cinemática de {20} en  . Al tratarse de un movimiento plano, la velocidad angular es perpendicular al plano director:
. Al tratarse de un movimiento plano, la velocidad angular es perpendicular al plano director:
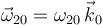
En el movimiento {20}, conocemos la velocidad (dato) del punto  y la velocidad (nula) del punto
y la velocidad (nula) del punto 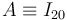 . Relacionando ambas velocidades entre sí mediante la ecuación del campo de velocidades del movimiento {20}, deducimos el valor de la correspondiente velocidad angular:
. Relacionando ambas velocidades entre sí mediante la ecuación del campo de velocidades del movimiento {20}, deducimos el valor de la correspondiente velocidad angular:
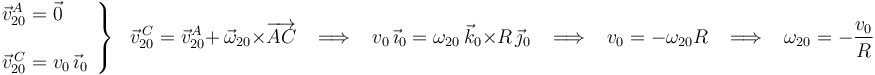
Por tanto:
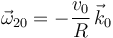
Ya podemos calcular la velocidad del punto  en el movimiento {20} mediante la ecuación del campo de velocidades de dicho movimiento:
en el movimiento {20} mediante la ecuación del campo de velocidades de dicho movimiento:
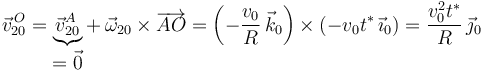
Así que ahora tenemos también la reducción cinemática de {20} en  :
:
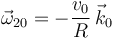 ;
; 
Y aplicando las leyes de composición, determinamos finalmente la reducción cinemática de {21} en  :
:
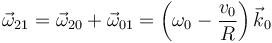 ;
; 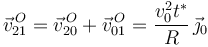
La posición exacta del C.I.R.{21} se obtiene con la fórmula habitual:
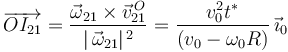
4 Aceleración instantánea del punto A en el movimiento {21}
Aplicando la ley de composición de aceleraciones (o teorema de Coriolis), la aceleración absoluta del punto  se puede calcular como suma de las aceleraciones relativa, de arrastre y de Coriolis de dicho punto:
se puede calcular como suma de las aceleraciones relativa, de arrastre y de Coriolis de dicho punto:
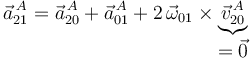
Observamos en primer lugar que el término de Coriolis se anula al ser  el C.I.R.{20}.
el C.I.R.{20}.
La aceleración relativa de  la podemos determinar a partir de la aceleración relativa del centro
la podemos determinar a partir de la aceleración relativa del centro  del disco utilizando la ecuación del campo de aceleraciones del movimiento {20}:
del disco utilizando la ecuación del campo de aceleraciones del movimiento {20}:
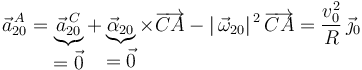
donde se ha tenido en cuenta que:
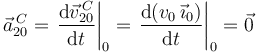 ;
; 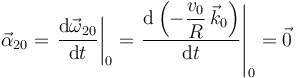
Y la aceleración de arrastre de  la calculamos a partir de la aceleración de arrastre del punto
la calculamos a partir de la aceleración de arrastre del punto  utilizando la ecuación del campo de aceleraciones del movimiento {01}:
utilizando la ecuación del campo de aceleraciones del movimiento {01}:
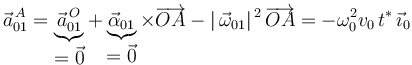
donde se ha tenido en cuenta que:
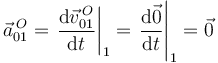 ;
; 
Así que, sustituyendo los valores obtenidos para 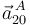 y
y 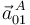 en la ley de composición de aceleraciones, se obtiene finalmente:
en la ley de composición de aceleraciones, se obtiene finalmente:
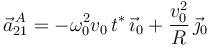
5 ¿En qué caso particular {21} es una traslación?
Examinando la reducción cinemática de {21} en el punto  (que fue calculada más arriba):
(que fue calculada más arriba):
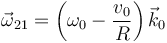 ;
; 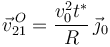
deducimos lo que tiene que ocurrir para que la velocidad angular del movimiento {21} se anule:
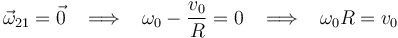
Así, pues, en el caso particular de que 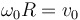 , el movimiento {21} es una traslación, ya que el campo de velocidades es uniforme y distinto de cero.
, el movimiento {21} es una traslación, ya que el campo de velocidades es uniforme y distinto de cero.