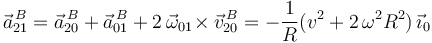No Boletín - Disco contenido en plano rotatorio II (Ex.Ene/20)
De Laplace
Contenido |
1 Enunciado
Mediante un par de revolución, el plano 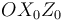 (sólido "0") rota alrededor del eje vertical fijo
(sólido "0") rota alrededor del eje vertical fijo 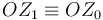 en el sentido indicado en la figura y con velocidad angular de módulo constante
en el sentido indicado en la figura y con velocidad angular de módulo constante  , de forma que el eje
, de forma que el eje 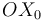 permanece siempre contenido en el plano horizontal fijo
permanece siempre contenido en el plano horizontal fijo  (sólido "1"). A su vez, un disco (sólido "2") de centro
(sólido "1"). A su vez, un disco (sólido "2") de centro  y radio
y radio  , contenido en todo instante en el plano
, contenido en todo instante en el plano 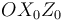 , rueda sin deslizar sobre el eje vertical
, rueda sin deslizar sobre el eje vertical 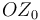 , moviéndose su centro
, moviéndose su centro  con velocidad relativa
con velocidad relativa 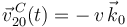 (donde
(donde  es una constante positiva). Sea
es una constante positiva). Sea 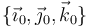 la base ortonormal asociada al triedro
la base ortonormal asociada al triedro 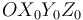 . Las cuestiones planteadas a continuación se refieren al instante representado en la figura, siendo
. Las cuestiones planteadas a continuación se refieren al instante representado en la figura, siendo  el punto de contacto entre el disco y el eje
el punto de contacto entre el disco y el eje 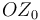 , y siendo
, y siendo  el punto del disco diametralmente opuesto al punto
el punto del disco diametralmente opuesto al punto  .
.
- ¿Dónde se halla el eje instantáneo de rotación del movimiento
 ?
?
- ¿Cuánto vale la velocidad
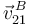 ?
?
- ¿Cuánto vale la aceleración
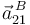 ?
?
2 Eje instantáneo de rotación del movimiento {20}
Conocemos las velocidades de dos puntos en el movimiento {20}: la del centro  del disco (dato del enunciado) y la del punto
del disco (dato del enunciado) y la del punto  de contacto entre el disco y el eje
de contacto entre el disco y el eje  (nula por no existir deslizamiento entre el disco y el eje
(nula por no existir deslizamiento entre el disco y el eje  ). Relacionando estas dos velocidades entre sí mediante la ecuación del campo de velocidades {20}, podemos deducir el valor de la velocidad angular
). Relacionando estas dos velocidades entre sí mediante la ecuación del campo de velocidades {20}, podemos deducir el valor de la velocidad angular 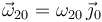 (nótese que la dirección propuesta para
(nótese que la dirección propuesta para 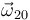 es la única compatible con que el disco permanezca contenido en todo instante en el plano
es la única compatible con que el disco permanezca contenido en todo instante en el plano 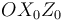 ):
):
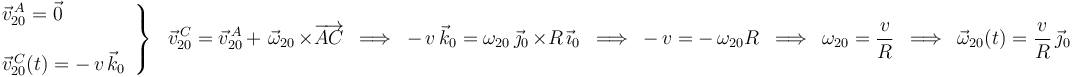
Obsérvese que el valor obtenido para la velocidad angular {20} tiene validez permanente en el tiempo, ya que en todo instante puede repetirse la deducción de este mismo valor relacionando la velocidad del centro del disco (conocida con carácter permanente) y la velocidad del punto de contacto disco-eje 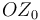 de ese instante.
de ese instante.
Como respuesta a la primera cuestión que plantea el problema, podemos afirmar que el eje instantáneo de rotación del movimiento  pasa por el punto
pasa por el punto  (cuya velocidad {20} es nula) y es paralelo al eje
(cuya velocidad {20} es nula) y es paralelo al eje 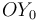 (dirección de la velocidad angular {20}).
(dirección de la velocidad angular {20}).
3 Caracterización de los movimientos elementales {01} y {20}
Los datos contenidos en el enunciado, junto a los resultados obtenidos en el apartado anterior, nos permiten expresar en la base vectorial 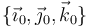 las reducciones cinemáticas del movimiento {01} (en el punto
las reducciones cinemáticas del movimiento {01} (en el punto  ) y del movimiento {20} (en el punto
) y del movimiento {20} (en el punto  ), así como un par de vectores geométricos que necesitaremos más adelante:
), así como un par de vectores geométricos que necesitaremos más adelante:
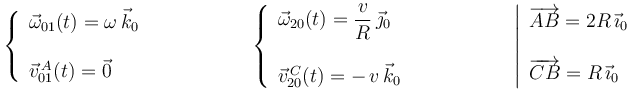
donde se ha tenido en cuenta que el punto  pertenece al eje permanente de rotación del movimiento {01} (eje
pertenece al eje permanente de rotación del movimiento {01} (eje 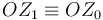 ), es decir, que se trata de un punto fijo en dicho movimiento (velocidad permanentemente nula).
), es decir, que se trata de un punto fijo en dicho movimiento (velocidad permanentemente nula).
Con vistas al cálculo de aceleraciones, resulta interesante determinar también en los movimientos {01} y {20} las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante:
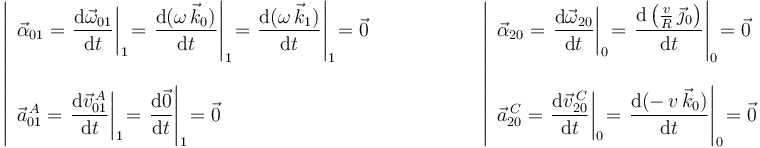
4 Velocidad instantánea {21} del punto B
Para determinar la velocidad 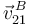 , calculamos primero las velocidades
, calculamos primero las velocidades 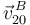 y
y 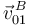 utilizando las ecuaciones de los campos de velocidades correspondientes:
utilizando las ecuaciones de los campos de velocidades correspondientes:
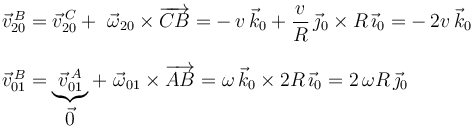
y, a continuación, aplicamos la ley de composición de velocidades en el punto  :
:
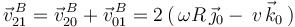
5 Aceleración instantánea {21} del punto B
Conforme a la ley de composición de aceleraciones (teorema de Coriolis), la aceleración 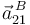 se calcula así:
se calcula así:
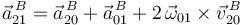
Necesitamos, por tanto, calcular previamente la aceleración 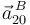 (mediante la ecuación del campo de aceleraciones {20}):
(mediante la ecuación del campo de aceleraciones {20}):
![\vec{a}^{\, B}_{20}=\underbrace{\vec{a}^{\, C}_{20}}_{\displaystyle\vec{0}}+\,\underbrace{\vec{\alpha}_{20}}_{\displaystyle\vec{0}}\times\,\overrightarrow{CB}\,+\,\vec{\omega}_{20}\times(\omega_{20}\times\overrightarrow{CB})=\displaystyle\frac{v}{R}\,\vec{\jmath}_0\times\left[\,\displaystyle\frac{v}{R}\,\vec{\jmath}_0\times R\,\vec{\imath}_0\right]=-\displaystyle\frac{v^2}{R}\,\vec{\imath}_0](/wiki/images/math/5/3/0/530371908c45b8136a8f163dbe6f3289.png)
la aceleración 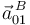 (mediante la ecuación del campo de aceleraciones {01}):
(mediante la ecuación del campo de aceleraciones {01}):
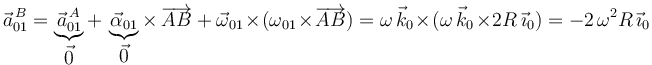
y el término de Coriolis (mediante su fórmula):
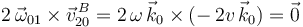
Sustituyendo en la ley de composición de aceleraciones, obtenemos por fin la aceleración 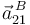 :
: