No Boletín - Disco con centro acelerado rodando sin deslizar (Ex.Ene/13)
De Laplace
1 Enunciado
Un disco de radio  , contenido en todo instante en el plano
, contenido en todo instante en el plano  , rueda sin deslizar sobre el eje
, rueda sin deslizar sobre el eje  . El centro
. El centro  del disco avanza en el sentido negativo del eje
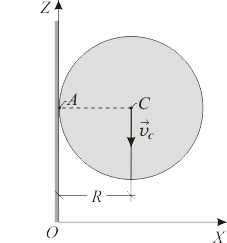
del disco avanza en el sentido negativo del eje  (ver figura) con una celeridad linealmente creciente con el tiempo
(ver figura) con una celeridad linealmente creciente con el tiempo 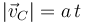 (donde
(donde  es una constante positiva conocida). Para el instante
es una constante positiva conocida). Para el instante  , al cual corresponde la posición del disco representada en la figura, se pregunta:
, al cual corresponde la posición del disco representada en la figura, se pregunta:
- ¿Cuánto vale la velocidad angular instantánea
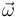 del disco?
del disco?
- ¿Y la aceleración instantánea
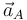 del punto del disco que se halla en contacto con el eje
del punto del disco que se halla en contacto con el eje 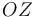 ?
?
2 Velocidad angular instantánea
El hecho de que el disco permanezca siempre contenido en el plano 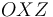 implica que su vector velocidad angular
implica que su vector velocidad angular 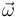 es perpendicular a dicho plano (porque si hubiese componentes de velocidad angular paralelas al plano, éstas sacarían al disco del plano). Por tanto:
es perpendicular a dicho plano (porque si hubiese componentes de velocidad angular paralelas al plano, éstas sacarían al disco del plano). Por tanto:
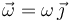
La velocidad del centro  del disco constituye un dato del ejercicio, ya que se nos han especificado su módulo, su dirección y su sentido:
del disco constituye un dato del ejercicio, ya que se nos han especificado su módulo, su dirección y su sentido:
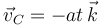
Por otra parte, se nos indica que el disco rueda sin deslizar sobre el eje  . La ausencia de deslizamiento implica que el punto de contacto disco-eje tiene velocidad instantánea nula:
. La ausencia de deslizamiento implica que el punto de contacto disco-eje tiene velocidad instantánea nula:
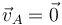
Conocemos, pues, las velocidades de los puntos  y
y  . Relacionando ambas velocidades entre sí mediante la ecuación del campo de velocidades, deducimos el valor de la velocidad angular instantánea del disco:
. Relacionando ambas velocidades entre sí mediante la ecuación del campo de velocidades, deducimos el valor de la velocidad angular instantánea del disco:
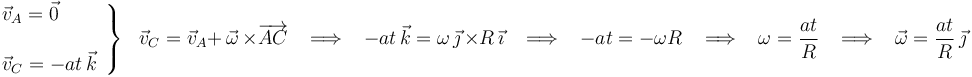
3 Aceleración instantánea del punto A
Al conocer la velocidad angular del disco como función del tiempo, podemos obtener la aceleración angular 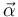 mediante derivación temporal:
mediante derivación temporal:

Análogamente, conocer la velocidad 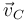 del centro del disco como función del tiempo nos permite obtener la aceleración
del centro del disco como función del tiempo nos permite obtener la aceleración 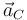 derivando:
derivando:
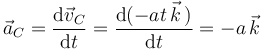
Por último, deducimos la aceleración instantánea 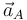 (del punto del disco que se halla en contacto con el eje
(del punto del disco que se halla en contacto con el eje 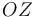 ) relacionándola con la aceleración
) relacionándola con la aceleración 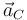 mediante la ecuación del campo de aceleraciones:
mediante la ecuación del campo de aceleraciones:
![\vec{a}_A=\vec{a}_C\,+\,\vec{\alpha}\,\times\,\overrightarrow{CA}\,+\,\vec{\omega}\,\times(\vec{\omega}\,\times\,\overrightarrow{CA})=-a\,\vec{k}\,+\,\underbrace{\frac{a}{R}\,\vec{\jmath}\,\times(-R\,\vec{\imath}\,)}_{a\,\vec{k}}+\,\frac{at}{R}\,\vec{\jmath}\,\,\times\underbrace{\left[\frac{at}{R}\,\vec{\jmath}\,\times(-R\,\vec{\imath}\,)\right]}_{at\,\vec{k}}=\frac{a^2t^2}{R}\,\vec{\imath}](/wiki/images/math/1/0/5/10587ce33a8b02f0c60166a5369498ff.png)
Nota: Nótese que habríamos llegado a un resultado erróneo si hubiésemos tratado de obtener 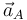 mediante la derivación temporal de la velocidad
mediante la derivación temporal de la velocidad 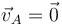 . Pero... ¿por qué no sería correcto hacer esto y, sin embargo, hemos obtenido
. Pero... ¿por qué no sería correcto hacer esto y, sin embargo, hemos obtenido 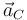 derivando respecto al tiempo
derivando respecto al tiempo 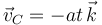 ? La razón es que
? La razón es que 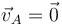 es un valor puramente instantáneo de la velocidad del punto
es un valor puramente instantáneo de la velocidad del punto  del disco, no es la velocidad de dicho punto como función del tiempo. De hecho,
del disco, no es la velocidad de dicho punto como función del tiempo. De hecho, 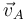 sólo vale cero en el instante en el que el punto
sólo vale cero en el instante en el que el punto  del disco se halla en contacto con el eje
del disco se halla en contacto con el eje  , pero no un segundo antes ni un segundo después. Por el contrario,
, pero no un segundo antes ni un segundo después. Por el contrario, 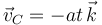 es la velocidad del centro
es la velocidad del centro  del disco como una función del tiempo.
del disco como una función del tiempo.