No Boletín - Cuestión sobre rodar, pivotar y deslizar (Ex.Sep/14)

De Laplace

1 Enunciado

Una esfera (sólido "2") se mueve sobre el plano 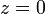$z=0\,$ (sólido "1") de cierto sistema de referencia OXYZ, manteniéndose en todo instante el contacto puntual esfera-plano. La reducción cinemática del movimiento {21} en el punto de contacto $C\,$ viene dada por:

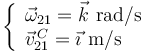
$\left\{\begin{array}{l} \vec{\omega}_{21}=\vec{k}\,\,\mathrm{rad}/\mathrm{s} \\ \vec{v}^{\, C}_{21}=\vec{\imath}\,\,\mathrm{m}/\mathrm{s} \end{array}\right.$

¿Cuál de las siguientes descripciones del movimiento de la esfera respecto al plano 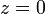$z=0\,$ es la correcta?

(a) Rodadura y pivotamiento, sin deslizamiento.

(b) Rodadura y deslizamiento, sin pivotamiento.

(c) Pivotamiento y deslizamiento, sin rodadura.

(d) Rodadura, pivotamiento y deslizamiento.

2 Solución

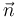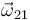Los conceptos de rodar, pivotar y deslizar aparecen en el contexto del movimiento relativo {21} entre dos sólidos que mantienen contacto puntual en todo instante. Se define un vector unitario $\vec{n}\,$ ortogonal al plano tangente común a las superficies de ambos sólidos en el punto de contacto $C\,$ . Descomponiendo la velocidad angular $\vec{\omega}_{21}\,$ y la velocidad del punto de contacto 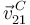$\vec{v}^{\, C}_{21}\,$ , respectivamente, como sendas sumas de un vector perpendicular a 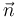$\vec{n}\,$ y otro vector paralelo a 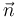$\vec{n}\,$ (con la fórmula deducida en la teoría), se introduce la siguiente terminología:

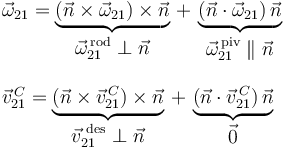
$\begin{array}{l} \vec{\omega}_{21}=\underbrace{(\vec{n}\times\vec{\omega}_{21})\times\vec{n}}_{\displaystyle\vec{\omega}_{21}^{\,\mathrm{rod}}\perp\vec{n}}\,+\,\underbrace{(\vec{n}\cdot\vec{\omega}_{21})\,\vec{n}}_{\displaystyle\vec{\omega}_{21}^{\,\mathrm{piv}}\parallel\vec{n}} \\ \\ \vec{v}^{\, C}_{21}=\underbrace{(\vec{n}\times\vec{v}^{\, C}_{21})\times\vec{n}}_{\displaystyle\vec{v}^{\,\,\mathrm{des}}_{21}\perp\vec{n}}\,+\,\underbrace{(\vec{n}\cdot\vec{v}^{\, C}_{21})\,\vec{n}}_{\displaystyle\vec{0}} \end{array}$

donde se denomina rodadura a la componente de rotación tangencial al contacto (perpendicular a 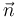$\vec{n}\,$ ), se denomina pivotamiento a la componente de rotación perpendicular al contacto (paralela a 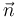$\vec{n}\,$ ), y se denomina deslizamiento a la traslación tangencial al contacto (perpendicular a 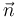$\vec{n}\,$ ). Obsérvese que no puede existir traslación perpendicular al contacto (paralela a 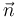$\vec{n}\,$ ) por ser incompatible con el mantenimiento del contacto puntual entre ambos sólidos.

Pues bien, aplicando las anteriores fórmulas al ejercicio que nos ocupa, obtenemos:

$\vec{\omega}_{21}=\vec{k}\,\,\mathrm{rad}/\mathrm{s} \,\,;\,\,\,\,\, \vec{v}^{\, C}_{21}=\vec{\imath}\,\,\mathrm{m}/\mathrm{s} \,\,;\,\,\,\,\, \vec{n}=\vec{k} \,\,\,\,\,\,\,\,\longrightarrow\,\,\, \left|\begin{array}{l} \vec{\omega}_{21}=\underbrace{(\vec{k}\times\vec{k}\,)\times\vec{k}}_{\displaystyle\vec{\omega}_{21}^{\,\mathrm{rod}}=\vec{0}}\,\,\,+\!\!\!\!\!\!\!\!\!\!\!\underbrace{(\vec{k}\cdot\vec{k}\,)\,\vec{k}}_{\,\,\,\,\,\,\,\,\,\,\,\,\displaystyle\vec{\omega}_{21}^{\,\mathrm{piv}}=\vec{k}\,\,\mathrm{rad}/\mathrm{s}} \\ \\ \vec{v}^{\, C}_{21}=\underbrace{(\vec{k}\times\vec{\imath}\,)\times\vec{k}}_{\displaystyle\vec{v}^{\,\,\mathrm{des}}_{21}=\vec{\imath}\,\,\mathrm{m}/\mathrm{s}}\,+\,\,\,\underbrace{(\vec{k}\cdot\vec{\imath}\,)\,\vec{k}}_{\displaystyle\vec{0}} \end{array}\right.$

Por tanto, la respuesta correcta es la (c): el movimiento de la esfera respecto al plano es de "pivotamiento y deslizamiento, sin rodadura".

No Boletín - Cuestión sobre rodar, pivotar y deslizar (Ex.Sep/14)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES