No Boletín - Cuestión sobre reacción vincular de aro liso (Ex.Feb/14)
De Laplace
1 Enunciado
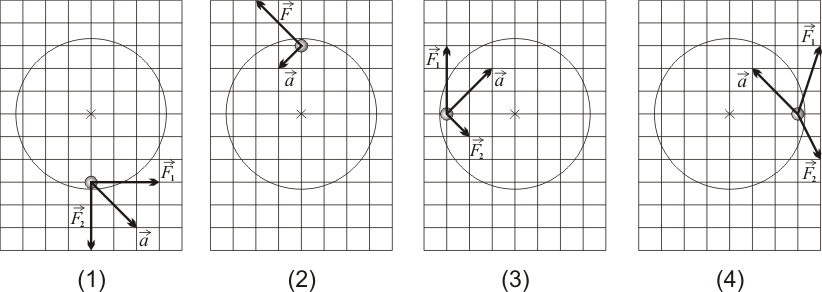
Una partícula material, de masa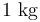 
, desliza sin rozamiento por el interior de un aro circular. En cierto
instante, se ha representado gráficamente la posición de la partícula, así como su aceleración y todas las fuerzas activas que soporta. Sin
embargo, se ha dejado sin representar la fuerza de reacción vincular que ejerce el aro liso sobre la partícula. La cuadrícula de los
diagramas corresponde a la unidad en el SI (Sistema Internacional) de cada magnitud vectorial.
¿Cuál de los siguientes diagramas es el correcto?
2 Solución
Según el enunciado, la única fuerza no representada en los diagramas es la fuerza de reacción vincular que ejerce el aro liso sobre la partícula. Pero esa fuerza vincular, a la que denominaremos 
, está relacionada con las fuerzas activas (sí representadas), y con la masa y la aceleración de la partícula mediante la segunda ley de Newton:
![\vec{F}_1\,+\,\vec{F}_2\,+\,\vec{\Phi}=m\vec{a}\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{[diagramas}\,\,\mathrm{(1),(3),(4)]}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\vec{F}+\,\vec{\Phi}=m\vec{a}\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{[diagrama}\,\,\mathrm{(2)]}](/wiki/images/math/4/0/6/406e64631edf1b37ac3e2998e283def6.png)
Despejando :
![\vec{\Phi}=m\vec{a}\,-\,\vec{F}_1\,-\,\vec{F}_2\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{[diagramas}\,\,\mathrm{(1),(3),(4)]}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\vec{\Phi}=m\vec{a}\,-\,\vec{F}\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{[diagrama}\,\,\mathrm{(2)]}](/wiki/images/math/b/e/3/be30c9ee15473e0257b00867be979d82.png)
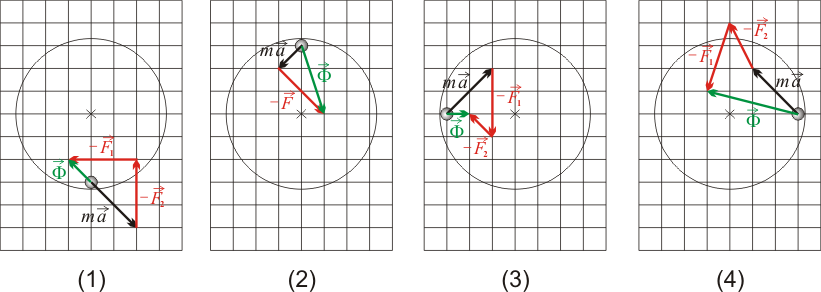
Así que, en cada diagrama, podemos obtener y representar la fuerza sumando vectorialmente al vector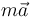 
los vectores opuestos de las fuerzas activas:
Obsérvese que, en cada nuevo diagrama, el vector 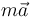(en color negro) coincide cuantitativamente con el vector 
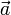del antiguo diagrama debido a que la masa de la partícula es 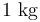. Se han dibujado en color rojo los vectores opuestos de las fuerzas activas, y en color verde el vector resultante de la suma vectorial del vector 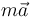con los vectores opuestos de las fuerzas activas.
Pero el enunciado nos dice que el aro es un vínculo liso, lo cual significa que es incapaz de ejercer una fuerza tangencial de rozamiento sobre la partícula. Eso quiere decir que la fuerza de reacción vincular tiene que ser necesariamente normal al aro (dirección radial de la circunferencia). Por tanto, el diagrama (3) es el correcto, ya que es el único en el que la fuerza (en color verde) posee la requerida dirección radial del aro.
