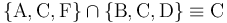No Boletín - Cuestión sobre curva de potencial V (Ex.Sep/14)

De Laplace

1 Enunciado

Una partícula se halla en el eje sometida a la acción de una fuerza conservativa. La función energía potencial 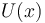y el nivel de energía mecánica 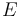de la partícula son los representados en la gráfica adjunta. ¿En qué posiciones está la partícula en reposo permanente?

2 Solución

¿Qué significa en términos cinemáticos estar en reposo permanente? Pues tener velocidad nula (reposo instantáneo) y aceleración nula (equilibrio, para que el reposo no sea meramente instantáneo sino permanente). Así que la partícula está en reposo permanente en la posición o posiciones en las que concurran estas dos circunstancias.

En la gráfica observamos la existencia de tres posiciones de reposo instantáneo (A, C y F), es decir, posiciones en las que coinciden los valores de energía potencial y energía mecánica de la partícula y en las que, por tanto, se anulan su energía cinética y su velocidad:

Y observamos la existencia de tres posiciones de equilibrio (B, C y D), es decir, posiciones en las que la función energía potencial presenta un extremo relativo (máximo o mínimo) y en las que, por tanto, se anulan la fuerza conservativa 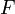(pendiente de la energía potencial cambiada de signo) y la aceleración de la partícula:

Hallando la intersección de estos dos conjuntos de posiciones, concluimos que la partícula está en reposo permanente sólo en la posición C: