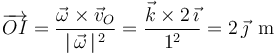No Boletín - Cuestión sobre cálculo gráfico del C.I.R. (Ex.Sep/15)

De Laplace

1 Enunciado

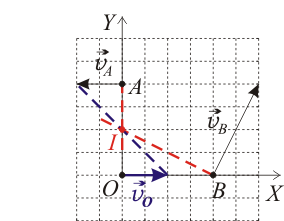
Sea 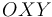$OXY\,$ el plano director en el movimiento plano de cierto sólido rígido. En el diagrama adjunto se representan las posiciones y velocidades de dos puntos ( $A\,$ y $B\,$ ) de dicho sólido en un instante dado. La cuadrícula del diagrama es tal que cada celdilla corresponde a la unidad en el SI (Sistema Internacional) de la magnitud representada.

Determine el vector de posición del centro instantáneo de rotación $I.\,$
Calcule la velocidad instantánea del punto del sólido rígido que se halla en $O\,$

2 Solución gráfica

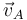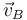Trazando sendas perpendiculares a las velocidades $\,\vec{v}_A\,$ y $\,\vec{v}_B\,$ en sus respectivos puntos, hallamos el centro instantáneo de rotación 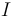$\,I\,$ en la intersección de ambas rectas (discontinuas de color rojo):

$\left.\begin{array}{l} \vec{v}_{A}\perp\overrightarrow{IA} \\ \\ \vec{v}_{B}\perp\overrightarrow{IB} \end{array}\right\} \,\,\,\,\,\Longrightarrow\,\,\,\,\, I\,\equiv\,\left\{\begin{array}{c} \mathrm{recta}\perp\vec{v}_{A} \\ \mathrm{que}\,\,\mathrm{pasa}\,\,\mathrm{por} \,\, A \end{array}\right\}\,\,\bigcap\,\,\left\{\begin{array}{c} \mathrm{recta}\perp\vec{v}_{B} \\ \mathrm{que}\,\,\mathrm{pasa}\,\,\mathrm{por} \,\, B \end{array}\right\}$

La posición de 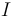$\,I\,$ obtenida en el diagrama por este procedimiento gráfico viene dada por el vector:

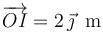
$\overrightarrow{OI}=2\,\vec{\jmath}\,\,\,\mathrm{m}$

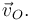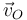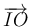Determinemos ahora gráficamente la velocidad $\,\vec{v}_O.\,$ Trazamos primero la recta-soporte de $\,\vec{v}_O\,$ , que es la perpendicular por $\,O\,$ al vector $\,\overrightarrow{IO}\,$ (ya que necesariamente 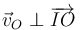$\vec{v}_{O}\perp\overrightarrow{IO}$ ). 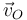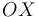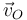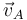Observamos entonces que la recta-soporte de $\,\vec{v}_O\,$ coincide con el eje $\,OX\,$ , y por tanto van a ser paralelas las velocidades $\,\vec{v}_O\,$ y $\,\vec{v}_A\,$ . Sabido que 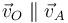$\,\vec{v}_O\parallel\vec{v}_A\,$ , localizamos el extremo de 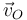$\,\vec{v}_O\,$ en la intersección de su recta-soporte (eje 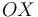$\,OX$ ) con la recta que pasa por el extremo de 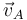$\,\vec{v}_A\,$ y por el punto 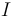$\,I\,$ (discontinua de color azul).

La velocidad 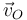$\,\vec{v}_O\,$ obtenida en el diagrama por este procedimiento gráfico viene dada por el vector:

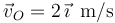
$\vec{v}_{O}=2\,\vec{\imath}\,\,\,\mathrm{m}\mathrm{/s}$

3 Solución analítica

El examen del diagrama nos permite conocer las velocidades de dos puntos del sólido rígido en el plano director:

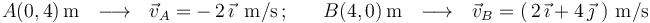
$A(0,4)\,\mathrm{m}\,\,\,\,\longrightarrow\,\,\,\,\vec{v}_A=-\,2\,\vec{\imath}\,\,\,\mathrm{m/s}\,; \,\,\,\,\,\,\,\,\,\, B(4,0)\,\mathrm{m}\,\,\,\,\longrightarrow\,\,\,\, \vec{v}_B=(\,2\,\vec{\imath}+4\,\vec{\jmath}\,\,)\,\,\mathrm{m/s}$

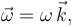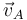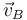La velocidad angular del sólido en movimiento plano es necesariamente perpendicular al plano director: $\,\vec{\omega}=\omega\,\vec{k},\,$ y su valor lo determinaremos al exigir que $\,\vec{v}_A\,$ y $\,\vec{v}_B\,$ satisfagan la ecuación del campo de velocidades:

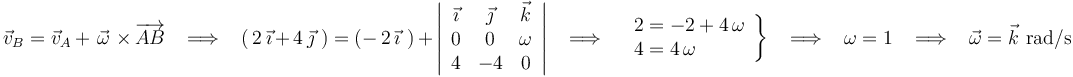
$\vec{v}_B=\vec{v}_A\,+\,\,\vec{\omega}\,\,\times\,\overrightarrow{AB}\,\,\,\,\,\Longrightarrow\,\,\,\,\, (\,2\,\vec{\imath}\,+\,4\,\vec{\jmath}\,\,)=(-\,2\,\vec{\imath}\,\,)\,+\,\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & \omega \\ 4 & -4 & 0 \end{array}\right|\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left.\begin{array}{l} 2=-2+4\,\omega \\ 4=4\,\omega \end{array}\right\}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\omega=1\,\,\,\,\,\Longrightarrow\,\,\,\,\,\vec{\omega}=\vec{k}\,\,\mathrm{rad}/\mathrm{s}$

Ahora ya podemos calcular la velocidad del punto $\,O\,$ del sólido aplicando nuevamente la ecuación del campo de velocidades:

$\vec{v}_O=\vec{v}_A\,+\,\,\vec{\omega}\,\,\times\overrightarrow{AO}=(-\,2\,\vec{\imath}\,\,)\,+\,\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & 1 \\ 0 & -4 & 0 \end{array}\right|=2\,\vec{\imath}\,\,\,\mathrm{m}\mathrm{/s}$

Y, por último, determinamos analíticamente la posición del centro instantáneo de rotación 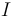$\,I\,$ mediante la fórmula estudiada en la teoría:

$\overrightarrow{OI}=\frac{\vec{\omega}\times\vec{v}_O}{|\,\vec{\omega}\,|^{\, 2}}=\frac{\vec{k}\times2\,\vec{\imath}}{1^{2}}=2\,\vec{\jmath}\,\,\,\mathrm{m}$

No Boletín - Cuestión sobre cálculo gráfico del C.I.R. (Ex.Sep/15)

De Laplace

1 Enunciado

2 Solución gráfica

3 Solución analítica

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES