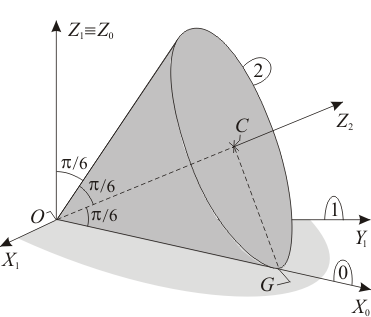
Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Cono sobre plano horizontal (Ex.Ene/18)

De Laplace

Contenido

1 Enunciado

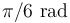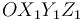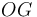Un cono recto (sólido "2"), con un semiángulo de \pi/6\,\,\mathrm{rad}\, en el vértice, rueda sin deslizar sobre el plano horizontal OX_1Y_1\, del triedro fijo OX_1Y_1Z_1\, (sólido "1"), manteniendo su vértice fijo en el punto O\, y teniendo en cada instante una generatriz OG\, en contacto con el citado plano horizontal. 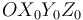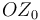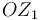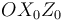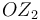Se define un triedro auxiliar móvil OX_0Y_0Z_0\, (sólido "0"), cuyo eje OZ_0\, coincide con el eje OZ_1\,, y cuyo plano OX_0Z_0\, contiene siempre al centro C\, de la base del cono y, por tanto, contiene también al eje de simetría OZ_2\, del cono. Se conoce como dato que 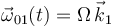\vec{\omega}_{01}(t)= \Omega\,\vec{k}_1\, (siendo 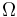\Omega\, una constante positiva). 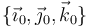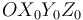Sea \{\vec{\imath}_0,\vec{\jmath}_0, \vec{k}_0\}\, la base ortonormal asociada al triedro OX_0Y_0Z_0\,.

  1. ¿Cuál es el eje instantáneo de rotación del movimiento \{21\}\,?
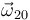  2. Determine la velocidad angular \vec{\omega}_{20}\,.
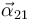  3. Determine la aceleración angular \vec{\alpha}_{21}\,.

2 Ejes de rotación de los movimientos {21}, {01} y {20}

Aunque sólo se pide el eje instantáneo de rotación del movimiento \{21\}\,, conviene determinar también los ejes de rotación de los movimientos \{01\}\, y \{20\}\,.

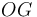Se nos dice que el cono (sólido "2") rueda sin deslizar sobre el plano horizontal OX_1Y_1\, (sólido "1"). La condición de no deslizamiento implica la nulidad de las velocidades instantáneas \{21\}\, de todos los puntos de la generatriz de contacto entre el cono y el plano OX_1Y_1\, (generatriz OG\,), lo que a su vez conlleva la pertenencia de dicha generatriz al eje instantáneo de rotación del movimiento \{21\}\,. Así pues, el eje instantáneo de rotación del movimiento \{21\}\, coincide con el eje OX_0\,:

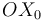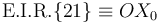
\mathrm{E.I.R.}\{21\}\equiv OX_0\,

tratándose de un eje instantáneo (y no permanente) de rotación al ser un eje móvil respecto al observador "1".

Dado que el eje OZ0 (sólido "0") es coincidente con el eje OZ1 (sólido "1"), es obvio que todos sus puntos están en reposo permanente en el movimiento \{01\}\, y constituyen el eje permanente de rotación del movimiento \{01\}\,:

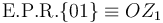
\mathrm{E.P.R.}\{01\}\equiv OZ_1\,

tratándose de un eje permanente de rotación al ser un eje fijo respecto al observador "1".

Por último, se observa que el eje de simetria 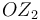OZ_2\, del cono (sólido "2") ocupa una posición fija en el triedro 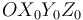OX_0Y_0Z_0\, (sólido "0"), de modo que todos sus puntos se hallan en reposo permanente en el movimiento \{20\}\, y constituyen el eje permanente de rotación del movimiento \{20\}\,:

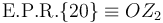
\mathrm{E.P.R.}\{20\}\equiv OZ_2\,

tratándose de un eje permanente de rotación al ser un eje fijo respecto al observador "0".

3 Velocidad angular del movimiento {20}

Aunque sólo se pide la velocidad angular del movimiento \{20\}\,, sin apenas esfuerzo adicional obtendremos también la velocidad angular del movimiento \{21\}\,.

Se conoce como dato la velocidad angular del movimiento \{01\}\,:

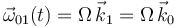
\vec{\omega}_{01}(t)= \Omega\,\vec{k}_1=\Omega\,\vec{k}_0\,

Por otra parte, sabemos que la velocidad angular de cada movimiento tiene necesariamente la dirección del eje de rotación de dicho movimiento. Por tanto:

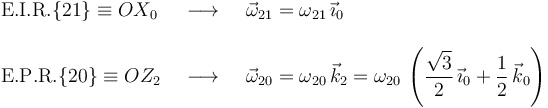
\begin{array}{lll}\mathrm{E.I.R.}\{21\}\equiv OX_0 & \,\,\,\longrightarrow\,\,\, & \vec{\omega}_{21}=\omega_{21}\,\vec{\imath}_0 \\ \\ \mathrm{E.P.R.}\{20\}\equiv OZ_2 & \,\,\,\longrightarrow\,\,\, & \vec{\omega}_{20}=\omega_{20}\,\vec{k}_2=\omega_{20}\,\left(\displaystyle\frac{\sqrt{3}}{2}\,\vec{\imath}_0+\frac{1}{2}\,\vec{k}_0\right) \end{array}

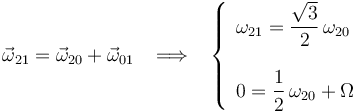
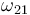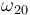Exigiendo el cumplimiento de la ley de composición de velocidades angulares y separando componentes en la base "0", se obtiene un sistema de dos ecuaciones para las incógnitas \omega_{21}\, y \omega_{20}\,:

\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\left\{\begin{array}{l} \omega_{21}=\displaystyle\frac{\sqrt{3}}{2}\,\omega_{20} \\ \\ 0=\displaystyle\frac{1}{2}\,\omega_{20}+\Omega \end{array}\right.

Resolviendo este sistema de ecuaciones, se obtienen las siguientes soluciones:

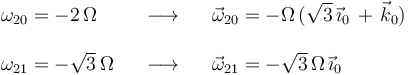
\begin{array}{lll}\omega_{20}=-2\,\Omega & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{\omega}_{20}=-\Omega\,(\sqrt{3}\,\vec{\imath}_0\,+\,\vec{k}_0) \\ \\ \omega_{21}=-\sqrt{3}\,\Omega & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{\omega}_{21}=-\sqrt{3}\,\Omega\,\vec{\imath}_0 \end{array}

4 Aceleración angular del movimiento {21}

Calculamos primero, mediante su definición, las aceleraciones angulares de los movimientos \{01\}\, y \{20\}\,:

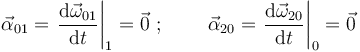
\vec{\alpha}_{01}=\left.\frac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1=\vec{0}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{\alpha}_{20}=\left.\frac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0=\vec{0}

y, a continuación, determinamos la aceleración angular del movimiento \{21\}\, mediante la ley de composición de aceleraciones angulares:

\vec{\alpha}_{21}=\underbrace{\vec{\alpha}_{20}}_{\displaystyle =\vec{0}}\,+\,\underbrace{\vec{\alpha}_{01}}_{\displaystyle =\vec{0}}\,+\,\vec{\omega}_{01}\times\,\vec{\omega}_{20}=\Omega\,\vec{k}_0\,\times\,[-\Omega\,(\sqrt{3}\,\vec{\imath}_0\,+\,\vec{k}_0)]= -\sqrt{3}\,\Omega^2\,\vec{\jmath}_0

También se puede calcular la aceleración angular del movimiento \{21\}\, derivando respecto al tiempo la velocidad angular del movimiento \{21\}\,:

\vec{\alpha}_{21}=\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1=\underbrace{\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_0}_{\displaystyle =\vec{0}}\,+\,\,\vec{\omega}_{01}\times\,\vec{\omega}_{21}=\Omega\,\vec{k}_0\times[-\sqrt{3}\,\Omega\,\vec{\imath}_0]=-\sqrt{3}\,\Omega^2\,\vec{\jmath}_0
Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Cono_sobre_plano_horizontal_(Ex.Ene/18)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 19:30, 22 feb 2018. - Esta página ha sido visitada 2.711 veces. - Aviso legal - Acerca de Laplace