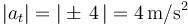No Boletín - Centro de curvatura y vector normal (Ex.Oct/18)

De Laplace

1 Enunciado

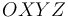El movimiento de una partícula $P\,$ es observado desde un triedro $OXYZ\,$ . Se conocen en un instante dado las posiciones de la partícula y del centro de curvatura 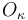$O_{\kappa}\,$ de su trayectoria, así como los módulos de su velocidad y su aceleración:

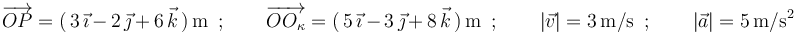
$\overrightarrow{OP}=(\,3\,\vec{\imath}\,-\,2\,\vec{\jmath}\,+\,6\,\vec{k}\,)\,\mathrm{m}\,\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\overrightarrow{OO_{\kappa}}=(\,5\,\vec{\imath}\,-\,3\,\vec{\jmath}\,+\,8\,\vec{k}\,)\,\mathrm{m}\,\,\,; \,\,\,\,\,\,\,\,\,\,\,\,|\vec{v}|=3\,\mathrm{m}/\mathrm{s}\,\,\,; \,\,\,\,\,\,\,\,\,\,\,\,|\vec{a}|=5\,\mathrm{m}/\mathrm{s}^2$

¿Cuál es el vector normal del triedro intrínseco de su trayectoria en dicho instante?
¿Cuánto vale (en valor absoluto) la componente tangencial de la aceleración de la partícula en dicho instante?

2 Vector normal

Según se ha visto en la teoría, el vector de posición del centro de curvatura de la trayectoria de una partícula $P\,$ en movimiento viene dado por la fórmula:

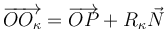
$\overrightarrow{OO_{\kappa}}=\overrightarrow{OP}+R_{\kappa}\vec{N}$

Por tanto, el conocimiento simultáneo de las posiciones instantáneas de la partícula y del centro de curvatura permite determinar directamente el vector 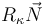$R_{\kappa}\vec{N}\,$ :

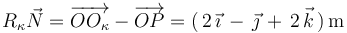
$R_{\kappa}\vec{N}=\overrightarrow{OO_{\kappa}}-\overrightarrow{OP}=(\,2\,\vec{\imath}\,-\,\vec{\jmath}\,+\,2\,\vec{k}\,)\,\mathrm{m}$

Tomando módulo de dicho vector, obtenemos el radio de curvatura instantáneo:

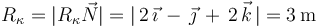
$R_{\kappa}=|R_{\kappa}\vec{N}|=|\,2\,\vec{\imath}\,-\,\vec{\jmath}\,+\,2\,\vec{k}\,|=3\,\mathrm{m}$

Y normalizando el vector 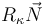$R_{\kappa}\vec{N}\,$ , obtenemos el vector normal del triedro intrínseco de la trayectoria en dicho instante:

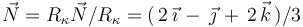
$\vec{N}=R_{\kappa}\vec{N}/R_{\kappa}=(\,2\,\vec{\imath}\,-\,\vec{\jmath}\,+\,2\,\vec{k}\,)/3$

3 Componente tangencial de la aceleración (en valor absoluto)

Conocidos el radio de curvatura y la celeridad (módulo de la velocidad), es inmediato calcular la componente normal de la aceleración de la partícula mediante la fórmula:

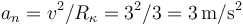
$a_n=v^2/R_{\kappa}=3^2/3=3\,\mathrm{m}/\mathrm{s}^2$

Por otra parte, el módulo de la aceleración de la partícula (también dado en el enunciado del ejercicio) se relaciona trivialmente con las componentes intrínsecas de la aceleración (tangencial y normal):

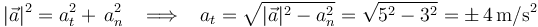
$|\vec{a}|^2=a_t^2+\,a_n^2\,\,\,\,\,\Longrightarrow\,\,\,\,\,a_t=\displaystyle\sqrt{|\vec{a}|^2-a_n^2}=\displaystyle\sqrt{5^2-3^2}=\pm\, 4\,\mathrm{m}/\mathrm{s}^2$

A partir de los datos del enunciado no podemos determinar si la componente tangencial de la aceleración es positiva o negativa, pero sí su valor absoluto:

$|a_t|=|\pm\, 4\,|=4\,\mathrm{m}/\mathrm{s}^2$

No Boletín - Centro de curvatura y vector normal (Ex.Oct/18)

De Laplace

1 Enunciado

2 Vector normal

3 Componente tangencial de la aceleración (en valor absoluto)

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES