No Boletín - Bola en canal rectilíneo (Ex.Sep/15)
De Laplace
1 Enunciado
Una bola (sólido "2") de radio 
se desplaza sobre dos carriles rectilíneos paralelos fijos (sólido "1") separados entre sí una distancia . El movimiento de la bola es tal que: i) en todo instante rueda sin deslizar sobre ambos carriles, y ii) su
centro 
realiza un movimiento rectilíneo y uniforme con celeridad 
. Llamamos 
y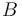 
respectivamente a los puntos de contacto entre la bola y cada uno de los carriles, y definimos el triedro fijo 
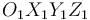de la figura.
- Determine el eje instantáneo de rotación del movimiento
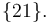
- Calcule la aceleración instantánea
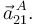
2 Eje instantáneo de rotación
Se nos dice que la bola (sólido "2") rueda sin deslizar sobre ambos carriles (sólido "1") en todo instante. La condición de no deslizamiento implica la nulidad de las velocidades instantáneas de los dos puntos de contacto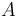 
y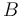 
, lo que a su vez conlleva la pertenencia de dichos puntos al eje instantáneo de rotación:
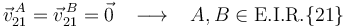
Así pues, el eje instantáneo de rotación del movimiento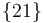 
es la recta que pasa por los puntos y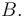 
3 Aceleración instantánea del punto A
Se nos dice también que el centro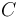 
de la bola realiza un movimiento rectilíneo y uniforme con celeridad . Esto implica que dicho punto 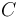tiene velocidad constante en el tiempo y, por tanto, aceleración nula:
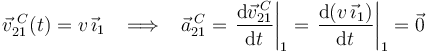
Nótese que la dirección de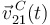 
(paralela al eje 
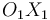) viene impuesta por el hecho de que el centro de la bola se moverá paralelamente al eje longitudinal del canal rectilíneo. Sin embargo, el sentido de 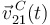no queda especificado en el enunciado, y nosotros lo hemos elegido arbitrariamente (sentido positivo del eje 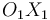) en la confianza de que dicha elección no influirá en el valor de la magnitud que se solicita.
Exigiendo que las velocidades de los puntos 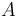y 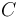de la bola satisfagan la ecuación del campo de velocidades, calculamos la velocidad angular 
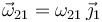de la bola (su dirección la conocemos a priori porque necesariamente 
):
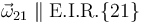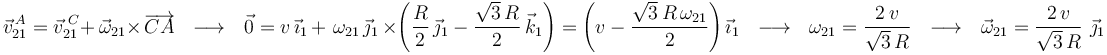
Dado que este mismo valor de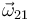 
se deduce de forma idéntica para cada instante de tiempo, se llega a la conclusión de que 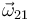es constante en el tiempo y que, por tanto, la aceleración angular 
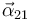de la bola es nula:
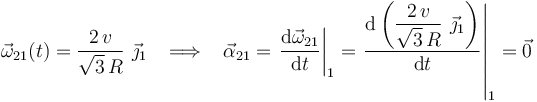
Finalmente, calculamos la aceleración del punto 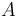de la bola utilizando la ecuación del campo de aceleraciones:
![\vec{a}^{\, A}_{21}=\underbrace{\vec{a}^{\, C}_{21}}_{=\,\vec{0}}+\,\underbrace{\vec{\alpha}_{21}}_{=\,\vec{0}}\times\,\overrightarrow{CA}\,+\,\,\vec{\omega}_{21}\,\times\,(\vec{\omega}_{21}\times\,\overrightarrow{CA}\,)=\frac{2\, v}{\sqrt{3}\,R}\,\,\vec{\jmath}_1\,\times\left[\frac{2\, v}{\sqrt{3}\,R}\,\,\vec{\jmath}_1\times\left(\frac{R}{2}\,\vec{\jmath}_1-\frac{\sqrt{3}\,R}{2}\,\vec{k}_1\right)\right]=\frac{2\,v^{\, 2}}{\sqrt{3}\,R}\,\vec{k}_1](/wiki/images/math/0/e/d/0ed508189554996695ab68f44ed99c50.png)
