No Boletín - Barra oblicua apoyada en disco (Ex.Dic/11)
De Laplace
1 Enunciado
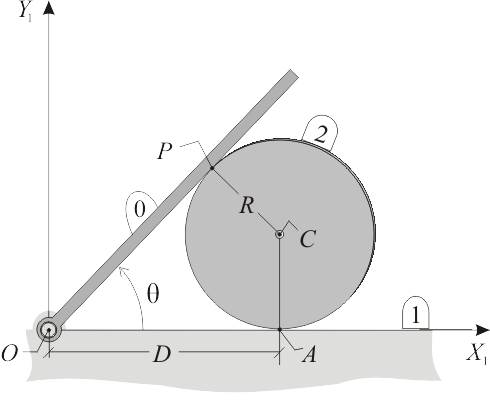
Se tiene un sistema de tres sólidos: una superficie horizontal fija (sólido "1"), una barra (sólido "0") articulada en un punto  de la superficie horizontal, y un disco
(sólido "2") de radio
de la superficie horizontal, y un disco
(sólido "2") de radio  . La barra se encuentra apoyada en el disco. El disco rueda sin deslizar sobre el suelo, moviéndose hacia la izquierda, empujando a la barra en su movimiento, de forma que el ángulo
. La barra se encuentra apoyada en el disco. El disco rueda sin deslizar sobre el suelo, moviéndose hacia la izquierda, empujando a la barra en su movimiento, de forma que el ángulo 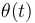 va aumentando (ver figura). Localice gráficamente las posiciones de los centros instantáneos de rotación
va aumentando (ver figura). Localice gráficamente las posiciones de los centros instantáneos de rotación  ,
, 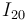 e
e 
Suponga que el disco tiene radio 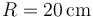 y que en un instante dado su punto de contacto con el suelo
y que en un instante dado su punto de contacto con el suelo  se encuentra a una distancia
se encuentra a una distancia 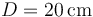 de
de  En ese momento el ángulo
En ese momento el ángulo  crece con derivada
crece con derivada 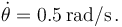 Para ese instante:
Para ese instante:
- Calcule las velocidades angulares
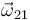 ,
, 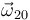 y
y 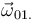
- Indique los vectores de posición, respecto al sistema de ejes "1", de los centros instantáneos de rotación.
- Halle la velocidad de deslizamiento del disco respecto a la barra en el punto de contacto
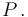
2 Localización gráfica de los centros instantáneos de rotación
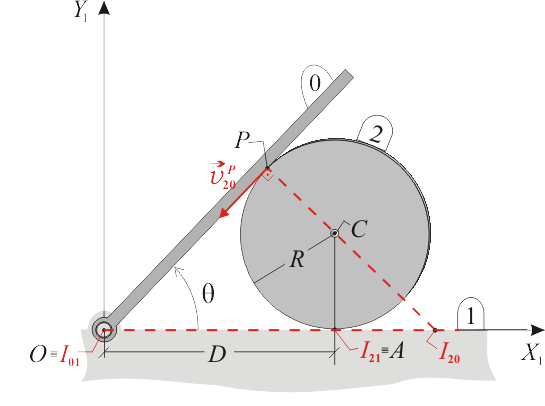
Se nos indica que el disco (sólido "2") rueda sin deslizar sobre el eje 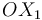 (sólido "1"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {21} coincide con el punto de contacto disco-eje:
(sólido "1"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {21} coincide con el punto de contacto disco-eje:
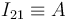
La barra (sólido "0") tiene un extremo articulado al origen  del eje
del eje 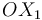 (sólido "1"). Por tanto, dicho punto
(sólido "1"). Por tanto, dicho punto  es un punto fijo (centro permanente de rotación) en el movimiento {01}:
es un punto fijo (centro permanente de rotación) en el movimiento {01}:
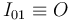
Dado que la barra (sólido "0") se halla apoyada en todo instante en el disco (sólido "2"), es obvio que el disco va a deslizar sobre la barra. La velocidad de deslizamiento disco-barra 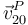 es necesariamente tangente al contacto, y tiene por tanto la dirección de la propia barra. Trazando la perpendicular a dicha velocidad en el punto
es necesariamente tangente al contacto, y tiene por tanto la dirección de la propia barra. Trazando la perpendicular a dicha velocidad en el punto  y trazando la recta que pasa por los puntos
y trazando la recta que pasa por los puntos 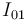 y
y  (en aplicación del teorema de los tres centros), hallaremos el punto
(en aplicación del teorema de los tres centros), hallaremos el punto 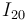 en la intersección de ambas rectas (ver I20 en la figura adjunta).
en la intersección de ambas rectas (ver I20 en la figura adjunta).
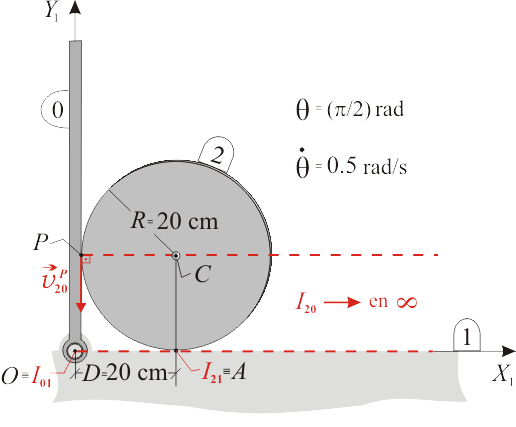
3 Particularización al instante en el que D=R
El resto del problema se refiere al instante concreto en el que el valor de la distancia  entre el punto
entre el punto  y el punto
y el punto  coincide exactamente con el valor del radio
coincide exactamente con el valor del radio  del disco (
del disco (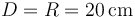 ). Es obvio (ver figura) que estamos hablando del instante en el que la barra se halla completamente vertical (
). Es obvio (ver figura) que estamos hablando del instante en el que la barra se halla completamente vertical (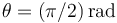 ). Nos dan también como dato el valor de
). Nos dan también como dato el valor de 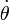 correspondiente a dicho instante (
correspondiente a dicho instante (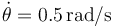 ).
).
Se nos piden los vectores de posición de los tres centros instantáneos de rotación para este instante particular. A eso podemos contestar ya, particularizando para el instante que ahora nos ocupa lo discutido en el apartado anterior:
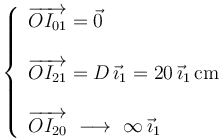
Para responder a las demás preguntas (las tres velocidades angulares y la velocidad de deslizamiento disco-barra), vamos ahora a plantear cuáles son las reducciones cinemáticas en el punto  de los movimientos {01}, {20} y {21}, y las incógnitas que nos veamos obligados a introducir se resolverán después exigiendo el cumplimiento de las leyes de composición de velocidades angulares y de velocidades.
de los movimientos {01}, {20} y {21}, y las incógnitas que nos veamos obligados a introducir se resolverán después exigiendo el cumplimiento de las leyes de composición de velocidades angulares y de velocidades.
La reducción cinemática de {01} en  se puede determinar sin introducir ninguna incógnita:
se puede determinar sin introducir ninguna incógnita:
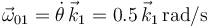 ;
; 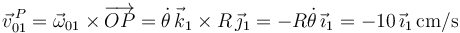
donde se ha tenido en cuenta que 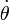 describe la rotación {01} al ser
describe la rotación {01} al ser  el ángulo formado por la barra (sólido "0") y el suelo (sólido "1"), y que el punto
el ángulo formado por la barra (sólido "0") y el suelo (sólido "1"), y que el punto  es el C.I.R.{01}.
es el C.I.R.{01}.
La reducción cinemática de {20} en  introduce dos incógnitas:
introduce dos incógnitas:
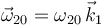 ;
; 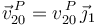
Por último, la reducción cinemática de {21} en  introduce una incógnita más:
introduce una incógnita más:
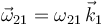 ;
; 
donde se ha tenido en cuenta que el punto  es el C.I.R.{21}.
es el C.I.R.{21}.
Y aplicando las leyes de composición, obtenemos tres ecuaciones para las tres incógnitas (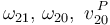 ):
):
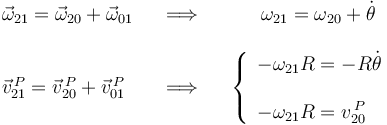
Resolviendo el sistema, se obtienen las soluciones:
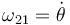 ;
; 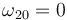 ;
; 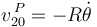
las cuales nos permiten, finalmente, responder al resto de las preguntas que nos hace el enunciado.
Las velocidades angulares son:
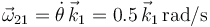 ;
;  ;
; 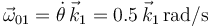
y la velocidad de deslizamiento del disco respecto a la barra es:

Obsérvese que la nulidad de 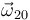 y la no nulidad de
y la no nulidad de 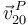 nos indican que {20} es en este instante particular una traslación, circunstancia que nos hace comprender que el C.I.R.{20} se escape hacia el infinito.
nos indican que {20} es en este instante particular una traslación, circunstancia que nos hace comprender que el C.I.R.{20} se escape hacia el infinito.