No Boletín - Barra deslizante en armazón rotatorio II (Ex.Feb/17)
De Laplace
1 Enunciado
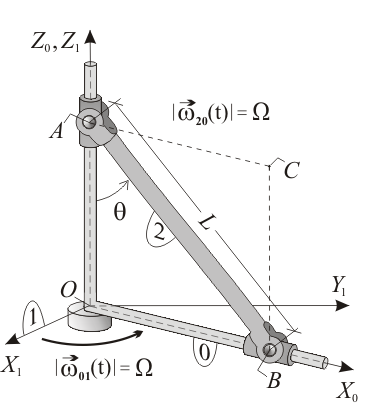
El armazón de barras paralelas a los ejes 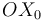 y
y 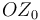 (sólido "0") rota alrededor del eje vertical fijo
(sólido "0") rota alrededor del eje vertical fijo 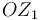 con velocidad angular de módulo constante
con velocidad angular de módulo constante 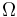 y en el sentido que se indica en la figura, permaneciendo el eje
y en el sentido que se indica en la figura, permaneciendo el eje 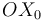 siempre contenido en el plano horizontal fijo
siempre contenido en el plano horizontal fijo  (sólido "1"). Mientras tanto, la varilla
(sólido "1"). Mientras tanto, la varilla 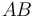 (sólido "2"), de longitud
(sólido "2"), de longitud  , desliza sus extremos
, desliza sus extremos  y
y  a lo largo de los ejes
a lo largo de los ejes 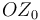 y
y 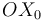 , respectivamente, de tal modo que su velocidad angular respecto al armazón de barras tiene módulo constante
, respectivamente, de tal modo que su velocidad angular respecto al armazón de barras tiene módulo constante 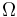 y el sentido correspondiente al crecimiento del ángulo
y el sentido correspondiente al crecimiento del ángulo  que se define en la figura. Sea
que se define en la figura. Sea 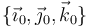 la base ortonormal asociada al triedro
la base ortonormal asociada al triedro 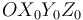 .
.
- ¿Por qué punto del plano
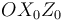 pasa el eje instantáneo de rotación del movimiento
pasa el eje instantáneo de rotación del movimiento  ?
?
- ¿Cuánto valen la velocidad
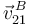 y la aceleración
y la aceleración 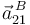 ?
?
2 Caracterización de los movimientos {01} y {20}
Los datos del enunciado nos permiten expresar en la base vectorial 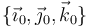 las reducciones cinemáticas del movimiento
las reducciones cinemáticas del movimiento  (en el punto
(en el punto  ) y del movimiento
) y del movimiento  (en el punto
(en el punto 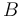 ):
):
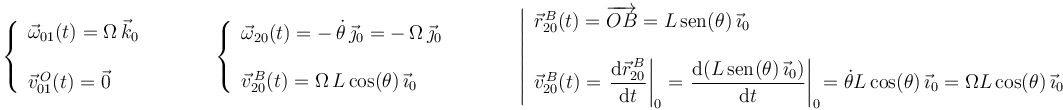
donde se ha tenido en cuenta que el punto  es un punto fijo en el movimiento
es un punto fijo en el movimiento  porque pertenece a su eje permanente de rotación (eje
porque pertenece a su eje permanente de rotación (eje 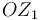 ), y que el extremo
), y que el extremo  de la varilla "2" es un punto cuyo vector de posición respecto al triedro "0" es fácilmente expresable para todo instante de tiempo, lo cual permite obtener
de la varilla "2" es un punto cuyo vector de posición respecto al triedro "0" es fácilmente expresable para todo instante de tiempo, lo cual permite obtener 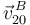 mediante derivación respecto al tiempo de
mediante derivación respecto al tiempo de 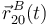 .
.
Nótese también en la expresión de 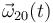 que, al decirnos el enunciado que la velocidad angular de la varilla respecto al armazón de barras tiene módulo constante
que, al decirnos el enunciado que la velocidad angular de la varilla respecto al armazón de barras tiene módulo constante 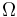 y el sentido correspondiente al crecimiento del ángulo
y el sentido correspondiente al crecimiento del ángulo  definido en la figura, llegamos a la conclusión de que
definido en la figura, llegamos a la conclusión de que 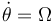 , igualdad que tendremos presente en lo que resta de solución.
, igualdad que tendremos presente en lo que resta de solución.
Con vistas al cálculo de aceleraciones, resulta interesante determinar también en los movimientos  y
y  las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante:
las aceleraciones angulares y las aceleraciones de aquellos puntos cuyas velocidades son conocidas en todo instante:
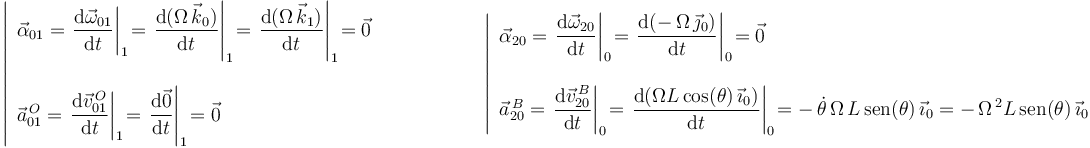
3 Eje instantáneo de rotación del movimiento {20}
El eje instantáneo de rotación del movimiento  (en adelante,
(en adelante, 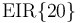 ) se obtiene a partir de su ecuación vectorial:
) se obtiene a partir de su ecuación vectorial:
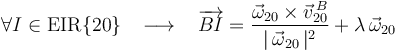
Y sustituyendo los valores previamente obtenidos de
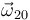 y
y 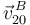 :
:
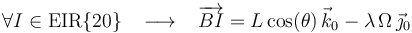
Obsérvese que 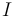 es un punto genérico del
es un punto genérico del 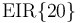 , pero el primer apartado del ejercicio nos pide un punto muy concreto del
, pero el primer apartado del ejercicio nos pide un punto muy concreto del 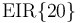 : el punto de dicho eje que pertenece al plano
: el punto de dicho eje que pertenece al plano 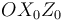 . Denominando
. Denominando 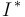 a dicho punto, es fácil comprobar que precisamente el primer término de la ecuación vectorial del
a dicho punto, es fácil comprobar que precisamente el primer término de la ecuación vectorial del 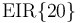 nos da la posición de
nos da la posición de 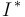 :
:
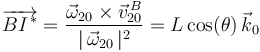
La posición obtenida nos indica que el punto pedido coincide con el denominado  en la figura del enunciado:
en la figura del enunciado:

4 Centro instantáneo de rotación del movimiento {20}
El procedimiento que acabamos de utilizar para determinar el punto 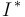 parte de la premisa de que aún no se ha estudiado el movimiento plano de sólidos rígidos. Ahora bien, el presente ejercicio formó parte de un examen en el que también entraba el movimiento plano. Por eso, nos parece conveniente señalar que la determinación del punto
parte de la premisa de que aún no se ha estudiado el movimiento plano de sólidos rígidos. Ahora bien, el presente ejercicio formó parte de un examen en el que también entraba el movimiento plano. Por eso, nos parece conveniente señalar que la determinación del punto 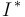 es bastante más directa si nos damos cuenta de que el movimiento
es bastante más directa si nos damos cuenta de que el movimiento  es un movimiento plano y de que, eligiendo el plano
es un movimiento plano y de que, eligiendo el plano 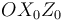 como plano director del mismo, el punto
como plano director del mismo, el punto 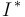 es precisamente el centro instantáneo de rotación
es precisamente el centro instantáneo de rotación 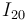 . Siendo así, los procedimientos de determinación gráfica del C.I.R. estudiados en el tema de movimiento plano nos permiten razonar como a continuación se hace.
. Siendo así, los procedimientos de determinación gráfica del C.I.R. estudiados en el tema de movimiento plano nos permiten razonar como a continuación se hace.
Conocemos la dirección de las velocidades 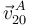 y
y 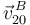 porque sabemos que los extremos de la varilla están obligados a moverse a lo largo de los ejes
porque sabemos que los extremos de la varilla están obligados a moverse a lo largo de los ejes 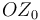 y
y 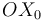 , respectivamente:
, respectivamente:

Trazamos la perpendicular a 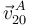 que pasa por
que pasa por  , y la perpendicular a
, y la perpendicular a 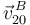 que pasa por
que pasa por  . El C.I.R.{20} (punto
. El C.I.R.{20} (punto 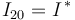 ) se halla en la intersección de las dos rectas que acabamos de trazar. Coincide, pues, con el punto
) se halla en la intersección de las dos rectas que acabamos de trazar. Coincide, pues, con el punto  de la figura del enunciado.
de la figura del enunciado.
5 Velocidad y aceleración {21} del punto B obtenidas por composición de movimientos
Para determinar la velocidad 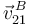 , calculamos primero la velocidad
, calculamos primero la velocidad 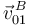 utilizando la ecuación del campo de velocidades
utilizando la ecuación del campo de velocidades 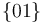 :
:
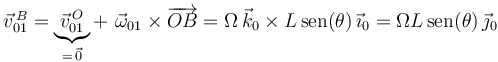
y, a continuación, aplicamos la ley de composición de velocidades en el punto  (observe que la velocidad
(observe que la velocidad 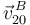 ya fue calculada al principio):
ya fue calculada al principio):
![\vec{v}^{\, B}_{21}=\vec{v}^{\, B}_{20}+\,\vec{v}^{\, B}_{01}=\Omega L\,[\,\mathrm{cos}(\theta)\,\vec{\imath}_0+
\mathrm{sen}(\theta)\,\vec{\jmath}_0\,]](/wiki/images/math/6/6/d/66d731bb603dfa9c2f9d133953ef8aa2.png)
Para determinar la aceleración 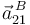 , calculamos primero la aceleración
, calculamos primero la aceleración 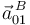 utilizando la ecuación del campo de aceleraciones
utilizando la ecuación del campo de aceleraciones 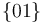 :
:
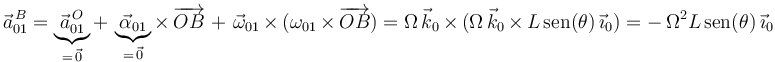
después calculamos el término de Coriolis:
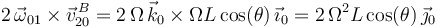
y, finalmente, aplicamos la ley de composición de aceleraciones en el punto  (observe que la aceleración
(observe que la aceleración 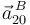 ya fue calculada al principio):
ya fue calculada al principio):
![\vec{a}^{\, B}_{21}=\vec{a}^{\, B}_{20}+\,\vec{a}^{\, B}_{01}+2\,\vec{\omega}_{01}\times\vec{v}^{\, B}_{20}=2\,\Omega^{\, 2}L\,[-\,\mathrm{sen}(\theta)\,\vec{\imath}_0+\mathrm{cos}(\theta)\,\vec{\jmath}_0\,]](/wiki/images/math/4/1/6/4168faa55a6e4dca5161ad79f9241d43.png)
6 Velocidad y aceleración {21} del punto B obtenidas por derivación temporal
El hecho de que el extremo  de la varilla "2" sea un punto cuyo vector de posición respecto al triedro "1" es fácilmente expresable para todo instante de tiempo:
de la varilla "2" sea un punto cuyo vector de posición respecto al triedro "1" es fácilmente expresable para todo instante de tiempo:
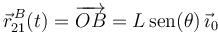
da pie a que también podamos obtener la velocidad y la aceleración de dicho punto en el movimiento  mediante sucesivas derivaciones respecto al tiempo (con ayuda de la fórmula general de Poisson y teniendo presente que
mediante sucesivas derivaciones respecto al tiempo (con ayuda de la fórmula general de Poisson y teniendo presente que 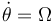 ):
):
![\left\{\begin{array}{l}
\vec{v}^{\, B}_{21}(t)=\left.\displaystyle\frac{\mathrm{d}\vec{r}^{\, B}_{21}}{\mathrm{d}t}\right|_1=\left.\displaystyle\frac{\mathrm{d}\vec{r}^{\, B}_{21}}{\mathrm{d}t}\right|_0+\,\vec{\omega}_{01}\times\vec{r}^{\, B}_{21}=\Omega L\,[\,\mathrm{cos}(\theta)\,\vec{\imath}_0+\mathrm{sen}(\theta)\,\vec{\jmath}_0\,] \\ \\
\vec{a}^{\, B}_{21}=\displaystyle\left.\frac{\mathrm{d}\vec{v}^{\, B}_{21}}{\mathrm{d}t}\right|_1=\left.\displaystyle\frac{\mathrm{d}\vec{v}^{\, B}_{21}}{\mathrm{d}t}\right|_0+\,\vec{\omega}_{01}\times\vec{v}^{\, B}_{21}=2\,\Omega^{\, 2}L\,[-\,\mathrm{sen}(\theta)\,\vec{\imath}_0+\mathrm{cos}(\theta)\,\vec{\jmath}_0\,]
\end{array}\right.](/wiki/images/math/c/3/4/c34491b5890d406047d6ad4be8712f2b.png)