No Boletín - Aro y varilla con un pasador (Ex.Ene/16)
De Laplace
Contenido |
1 Enunciado
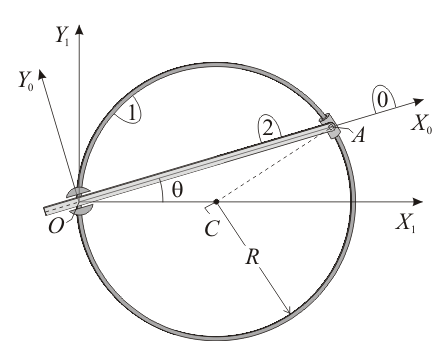
Sea una varilla rígida (sólido "2") que se mueve, en un plano fijo  (sólido "1"), de tal modo que está obligada a deslizar en todo instante por el interior de un pasador giratorio situado en el punto
(sólido "1"), de tal modo que está obligada a deslizar en todo instante por el interior de un pasador giratorio situado en el punto  , y además se halla articulada en su extremo
, y además se halla articulada en su extremo  a un deslizador que recorre un aro fijo (sólido "1") de radio
a un deslizador que recorre un aro fijo (sólido "1") de radio  y centro en el punto
y centro en el punto  (de posición
(de posición 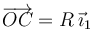 ).
).
Se define también la escuadra auxiliar 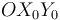 (sólido "0") de la figura, cuyo eje
(sólido "0") de la figura, cuyo eje 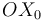 es colineal con la varilla en todo instante, y en cuya base asociada
es colineal con la varilla en todo instante, y en cuya base asociada 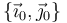 deberán expresarse todas las magnitudes vectoriales solicitadas en este ejercicio.
deberán expresarse todas las magnitudes vectoriales solicitadas en este ejercicio.
Denominando  al ángulo que forma la varilla con el eje
al ángulo que forma la varilla con el eje 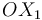 (ver figura), y sabiendo que
(ver figura), y sabiendo que
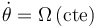 , se pide:
, se pide:
- Determinación gráfica (razonada) de las posiciones de los centros instantáneos de rotación
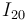 ,
, 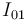 e
e 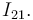
- Cálculo de las velocidades
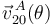 ,
, 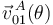 y
y 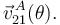
- Cálculo de las aceleraciones
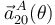 ,
, 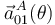 y
y 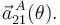
- Cálculo de la velocidad
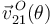 y la aceleración
y la aceleración 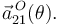
- Determinación analítica de la posición del centro instantáneo de rotación
 , es decir,
, es decir, 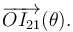
2 Determinación gráfica de los tres centros instantáneos de rotación
La escuadra auxiliar 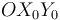 (sólido "0") y la escuadra fija
(sólido "0") y la escuadra fija  (sólido "1") comparten el punto
(sólido "1") comparten el punto  como origen. Por tanto,
como origen. Por tanto,  es un punto fijo (centro permanente de rotación) en el movimiento
es un punto fijo (centro permanente de rotación) en el movimiento  :
:
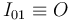
El eje 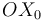 (sólido "0") se define colineal en todo instante con la varilla (sólido "2"), lo cual implica que el movimiento
(sólido "0") se define colineal en todo instante con la varilla (sólido "2"), lo cual implica que el movimiento  es una traslación permanente en dirección paralela a dicho eje
es una traslación permanente en dirección paralela a dicho eje 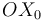 . Y como el centro instantáneo de rotación de una traslación plana se halla en el infinito en la dirección perpendicular a la dirección de la traslación, se concluye que:
. Y como el centro instantáneo de rotación de una traslación plana se halla en el infinito en la dirección perpendicular a la dirección de la traslación, se concluye que:
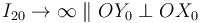
En lo que se refiere al movimiento  , conocemos a priori las direcciones de las velocidades de dos puntos de la varilla:
, conocemos a priori las direcciones de las velocidades de dos puntos de la varilla: 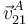 es tangente al aro fijo (porque el extremo
es tangente al aro fijo (porque el extremo  de la varilla está obligado a recorrer dicho aro), y
de la varilla está obligado a recorrer dicho aro), y 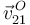 es tangente a la varilla (porque la misma está obligada a deslizar por el interior del pasador orientable ubicado en el punto
es tangente a la varilla (porque la misma está obligada a deslizar por el interior del pasador orientable ubicado en el punto  ). Trazando sendas perpendiculares a dichas velocidades en sus respectivos puntos, hallaremos el punto
). Trazando sendas perpendiculares a dichas velocidades en sus respectivos puntos, hallaremos el punto  en la intersección de ambas rectas:
en la intersección de ambas rectas:

Nótese que la recta perpendicular a 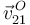 que pasa por el punto
que pasa por el punto  también podría haberse trazado apelando al cumplimiento del teorema de los tres centros, según el cual el punto
también podría haberse trazado apelando al cumplimiento del teorema de los tres centros, según el cual el punto  tiene que estar alineado con los puntos
tiene que estar alineado con los puntos 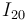 e
e 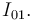
3 Cálculo de las tres velocidades del punto A
Al ser  el ángulo formado por la varilla (sólido "2") y el eje
el ángulo formado por la varilla (sólido "2") y el eje 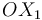 (sólido "1"), la velocidad angular
(sólido "1"), la velocidad angular
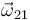 es igual a
es igual a 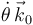 (con signo positivo porque a
(con signo positivo porque a 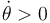 correspondería una rotación antihoraria). Pero
correspondería una rotación antihoraria). Pero  es también el ángulo formado por el eje
es también el ángulo formado por el eje 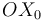 (sólido "0") y el eje
(sólido "0") y el eje 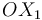 (sólido "1"), de tal modo que la velocidad angular
(sólido "1"), de tal modo que la velocidad angular 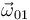 tiene el mismo valor que la
tiene el mismo valor que la 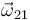 , lo cual es coherente (conforme a la ley de composición de velocidades angulares) con el hecho de que la velocidad angular
, lo cual es coherente (conforme a la ley de composición de velocidades angulares) con el hecho de que la velocidad angular 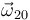 es nula (porque el movimiento
es nula (porque el movimiento  es una traslación). Así que, teniendo en cuenta que
es una traslación). Así que, teniendo en cuenta que 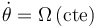 , se concluye:
, se concluye:
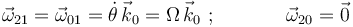
La velocidad 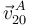 se puede obtener a partir de su definición:
se puede obtener a partir de su definición:
![\vec{v}^{A}_{20}=\displaystyle\left.\frac{d\vec{r}^{\, A}_{20}}{d t}\right|_0=\left.\frac{d\left[\,2R\,\mathrm{cos}(\theta)\,\vec{\imath}_0\,\right]}{d t}\right|_0=-2R\,\dot{\theta}\,\mathrm{sen}(\theta)\,\vec{\imath}_0=-2\,\Omega R\,\mathrm{sen}(\theta)\,\vec{\imath}_0](/wiki/images/math/5/e/8/5e88184930034fc54c2f3061e8ce7f88.png)
donde la expresión del vector 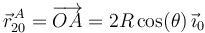 se ha deducido por simple inspección de las razones trigonométricas en el triángulo rectángulo
se ha deducido por simple inspección de las razones trigonométricas en el triángulo rectángulo 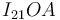 (cuyo ángulo interno en el vértice
(cuyo ángulo interno en el vértice  sabemos que vale
sabemos que vale  por ser isósceles el triángulo
por ser isósceles el triángulo 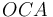 ).
).
Por otra parte, conocidos el valor de 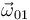 y la posición del C.I.R.
y la posición del C.I.R. (
(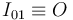 ), la velocidad
), la velocidad 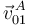 se obtiene mediante la ecuación del campo de velocidades del movimiento
se obtiene mediante la ecuación del campo de velocidades del movimiento  :
:
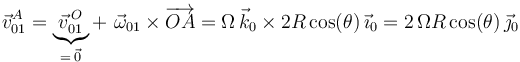
Finalmente, la ley de composición de velocidades permite deducir el valor de la velocidad 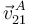 :
:
![\vec{v}^{\, A}_{21}=\vec{v}^{\, A}_{20}+\vec{v}^{\, A}_{01}=2\,\Omega R\left[-\mathrm{sen}(\theta)\,\vec{\imath}_0+\mathrm{cos}(\theta)\,\vec{\jmath}_0\,\right]](/wiki/images/math/4/d/2/4d2bbcc85cd05a9c783d8fb970389a51.png)
4 Cálculo de las tres aceleraciones del punto A
La aceleración 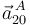 se puede obtener a partir de su definición:
se puede obtener a partir de su definición:
![\vec{a}^{\, A}_{20}=\displaystyle\left.\frac{d\vec{v}^{\, A}_{20}}{d t}\right|_0=\left.\frac{d\left[-2\,\Omega
R\,\mathrm{sen}(\theta)\,\vec{\imath}_0\,\right]}{d t}\right|_0=-2\,\Omega R\,\dot{\theta}\,\mathrm{cos}(\theta)\,\vec{\imath}_0=-2\,\Omega^2
R\,\mathrm{cos}(\theta)\,\vec{\imath}_0](/wiki/images/math/d/8/6/d861ebde44789216968bcc61859762df.png)
Deducimos la aceleración 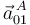 relacionándola con la
relacionándola con la 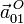 mediante la ecuación del campo de aceleraciones del movimiento {01}:
mediante la ecuación del campo de aceleraciones del movimiento {01}:
![\vec{a}^{\, A}_{01}=\underbrace{\vec{a}^{\, O}_{01}}_{=\,\vec{0}}+\underbrace{\vec{\alpha}_{01}}_{=\,\vec{0}}\times\,\overrightarrow{OA}-|\vec{\omega}_{01}|^2\,\overrightarrow{OA}=-\Omega^2\,[\,2R\,\mathrm{cos}(\theta)\,\vec{\imath}_0\,]=-2\,\Omega^2R\,\mathrm{cos}(\theta)\,\vec{\imath}_0](/wiki/images/math/f/5/f/f5fae9d91b59a023bcfc154e30674479.png)
donde se ha tenido en cuenta que 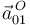 es nula por ser
es nula por ser  un punto fijo en el movimiento
un punto fijo en el movimiento  , y
, y 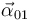 es nula por ser
es nula por ser 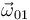 constante en el tiempo.
constante en el tiempo.
Por último, calculamos el término de Coriolis:
![2\,\vec{\omega}_{01}\times\vec{v}^{\, A}_{20}=2\,\Omega\,\vec{k}_0\times[-2\,\Omega R\,\mathrm{sen}(\theta)\,\vec{\imath}_0\,]=-\,4\,\Omega^2
R\,\mathrm{sen}(\theta)\,\vec{\jmath}_0](/wiki/images/math/f/b/b/fbb524183a368fbdea7fc704f43cd444.png)
y determinamos la aceleración 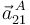 aplicando la ley de composición de aceleraciones:
aplicando la ley de composición de aceleraciones:
![\vec{a}^{\, A}_{21}=\vec{a}^{\, A}_{20}+\vec{a}^{\, A}_{01}+2\,\vec{\omega}_{01}\times\vec{v}^{\, A}_{20}=-\,4\,\Omega^2 R\left[\,\mathrm{cos}(\theta)\,\vec{\imath}_0+\mathrm{sen}(\theta)\,\vec{\jmath}_0\,\right]](/wiki/images/math/4/6/4/464e5f87c9f22f8b698fdaada8076cb3.png)
5 Cálculo de la velocidad y la aceleración del punto O en el movimiento {21}
Obtenemos la velocidad 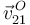 relacionándola con la
relacionándola con la 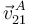 mediante la ecuación del campo de velocidades del movimiento
mediante la ecuación del campo de velocidades del movimiento  :
:
![\vec{v}^{\, O}_{21}=\vec{v}^{\, A}_{21}\,+\,\,\vec{\omega}_{21}\times\overrightarrow{AO}=2\,\Omega R\left[-\mathrm{sen}(\theta)\,\vec{\imath}_0+\mathrm{cos}(\theta)\,\vec{\jmath}_0\,\right]+\,\Omega\,\vec{k}_0\,\times[-2R\,\mathrm{cos}(\theta)\,\vec{\imath}_0\,]=
-2\,\Omega R\,\mathrm{sen}(\theta)\,\vec{\imath}_0](/wiki/images/math/f/2/b/f2bdc0e9b109e911d1bd608a46560606.png)
donde se ha utilizado que 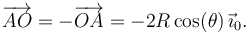
Obtenemos la aceleración 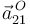 relacionándola con la
relacionándola con la 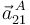 mediante la ecuación del
campo de aceleraciones del movimiento
mediante la ecuación del
campo de aceleraciones del movimiento  :
:
![\vec{a}^{\, O}_{21}=\vec{a}^{\, A}_{21}\,+\,\underbrace{\vec{\alpha}_{21}}_{=\,\vec{0}}\times\,\overrightarrow{AO}\,-\,|\vec{\omega}_{21}|^2\,\overrightarrow{AO}=-4\,\Omega^2 R\left[\,\mathrm{cos}(\theta)\,\vec{\imath}_0+\mathrm{sen}(\theta)\,\vec{\jmath}_0\,\right]\,+\,2\,\Omega^2R
\,\mathrm{cos}(\theta)\,\vec{\imath}_0=-2\,\Omega^2R\left[\,\mathrm{cos}(\theta)\,\vec{\imath}_0+2\,\mathrm{sen}(\theta)\,\vec{\jmath}_0\,\right]](/wiki/images/math/3/3/8/3382559c41f0b225015a7748e049f1b9.png)
donde se ha tenido en cuenta que 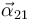 es nula por ser
es nula por ser 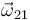 constante en el tiempo.
constante en el tiempo.
6 Determinación analítica del C.I.R.{21}
La posición del centro instantáneo de rotación  respecto al punto
respecto al punto  se determina mediante la fórmula:
se determina mediante la fórmula:
![\overrightarrow{OI_{21}}=\frac{\vec{\omega}_{21}\times\vec{v}^{\, O}_{21}}{|\,\vec{\omega}_{21}|^{2}}=\frac{\Omega\,\vec{k}_0\times[-2\,\Omega R\,\mathrm{sen}(\theta)\,\vec{\imath}_0\,]}{\Omega^2}=-2R\,\mathrm{sen}(\theta)\,\vec{\jmath}_{0}](/wiki/images/math/d/1/3/d13f520e595808a683663120e02daa11.png)