Muelle sobre un plano horizontal Primera Prueba de Control (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Velocidad areolar
- 2.2 Curvatura si

1 Enunciado

Una partícula de masa $m$ se mueve sobre un plano horizontal sin rozamiento. La partícula está enganchada a un muelle anclado en el origen de coordenadas, de constante $k$ y longitud natural nula. En el instante inicial, la partícula está situada sobre el eje $O X$ a una distancia $a$ del origen y con una velocidad 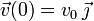$\vec{v}(0) = v_0\,\vec{\jmath}$ .

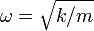Calcula la velocidad areolar de la partícula en cualquier instante de tiempo ( $\omega=\sqrt{k/m}$ ).
En el caso en que $v_0=a\,\omega$ , ¿cuál es la curvatura de la trayectoria en todo instante de tiempo?

2 Solución

2.1 Velocidad areolar

La partícula se mueve sobre un plano horizontal sin rozamiento. Como no se habla de la gravedad la fuerza gravitatoria no actúa. (Otro razonamiento posible es que la fuerza de reacción vincular del plano compensa en todo instante el peso de la partícula). Al ser el vínculo liso la única fuerza que actúa sobre la partícula es la del muelle. El punto de enganche es el origen, y su longitud natural es nula. Por tanto, la fuerza que el muelle ejerce sobre la partícula en cada instante es

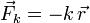
$\vec{F}_k = -k\,\vec{r}$

donde $\vec{r}$ es el vector de posición de la partícula. Esta fuerza es central, pues siempre apunta hacia el origen. Por tanto el momento angular de la partícula respecto del origen se conserva y es igual al que tiene en el instante inicial. Este momento vale

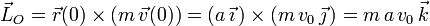
$\vec{L}_O = \vec{r}(0)\times(m\,\vec{v}(0)) = (a\,\vec{\imath}\,) \times(m\,v_0\,\vec{\jmath}\,) = m\,a\,v_0\,\vec{k}$

Por otra parte la velocidad areolar es proporcional al momento angular. Por tanto, la velocidad areolar de la partícula es

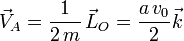
$\vec{V}_A = \dfrac{1}{2\,m}\,\vec{L}_O = \dfrac{a\,v_0}{2}\vec{k}$

y su módulo es

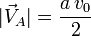
$|\vec{V}_A| = \dfrac{a\,v_0}{2}$

2.2 Curvatura si $v_0=a\,\omega$

La ecuación diferencial que determina el movimiento de la partícula es

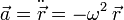
$\vec{a} = \ddot{\vec{r}} = -\omega^2\,\vec{r}$

con 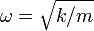$\omega = \sqrt{k/m}$ . La solución de esta ecuación puede escribirse de la forma

$\vec{r}(t) = \vec{A}\,\cos(\omega t) + \vec{B}\mathrm{sen}\,(\omega t)$

Los vectores constantes $\vec{A}$ y $\vec{B}$ se determinan a partir de las condiciones iniciales

$\vec{r}(0) = a\,\vec{\imath} \qquad \qquad \vec{v}=v_0\,\vec{\jmath}$

Tenemos

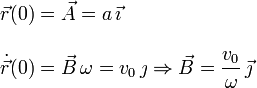
$\begin{array}{l} \vec{r}(0) = \vec{A} = a\,\vec{\imath} \\ \\ \dot{\vec{r}}(0) = \vec{B}\,\omega= v_0\,\jmath \Rightarrow \vec{B} = \dfrac{v_0}{\omega}\,\vec{\jmath} \end{array}$

Así pues la posición y la velocidad de la partícula en cada instante es

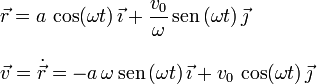
$\begin{array}{l} \vec{r} = a\,\cos(\omega t)\,\vec{\imath} + \dfrac{v_0}{\omega}\,\mathrm{sen}\,(\omega t)\,\vec{\jmath} \\ \\ \vec{v}=\dot{\vec{r}} = -a\,\omega\,\mathrm{sen}\,(\omega t)\,\vec{\imath} + v_0 \,\cos(\omega t)\,\vec{\jmath} \end{array}$

Si aplicamos la condición del enunciado tenemos

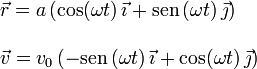
$\begin{array}{l} \vec{r} = a\,(\cos(\omega t)\,\vec{\imath} + \mathrm{sen}\,(\omega t)\,\vec{\jmath}) \\ \\ \vec{v}= v_0\,(-\mathrm{sen}\,(\omega t)\,\vec{\imath} + \cos(\omega t)\,\vec{\jmath}) \end{array}$

Hay varias formas de responder a la pregunta.

2.2.1 Cálculo directo

Podemos calcular la curvatura en cada punto usando la fórmula que nos da su valor

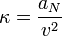
$\kappa = \dfrac{a_N}{v^2}$

En nuestro caso el módulo de la velocidad es constante

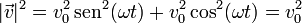
$|\vec{v}|^2 = v_0^2\,\mathrm{sen}^2(\omega t) + v_0^2\cos^2(\omega t) = v_0^2$

Para obtener la aceleración podemos derivar en la velocidad o, a partir de la ecuación diferencial observar que

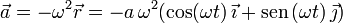
$\vec{a} = -\omega^2\vec{r} = -a\,\omega^2(\cos(\omega t)\,\vec{\imath} + \mathrm{sen}\,(\omega t)\,\vec{\jmath} )$

La componente normal es

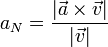
$a_N = \dfrac{|\vec{a}\times\vec{v}|}{|\vec{v}|}$

El producto vectorial es

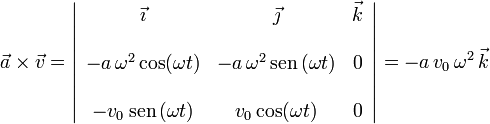
$\vec{a}\times\vec{v} = \left| \begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ &&\\ -a\,\omega^2\cos(\omega t) & -a\,\omega^2\,\mathrm{sen}\,(\omega t) & 0\\ &&\\ -v_0\,\mathrm{sen}\,(\omega t) & v_0\cos(\omega t) & 0 \end{array} \right| = -a\,v_0\,\omega^2\,\vec{k}$

Por tanto la aceleración normal es

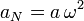
$a_N = a\,\omega^2$

Y la curvatura es

$\kappa = \dfrac{1}{a}$

2.2.2 Usando el momento angular

Podemos abreviar el cálculo anterior utilizando el momento angular calculado en el apartado anterior. La curvatura es

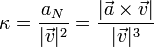
$\kappa = \dfrac{a_N}{|\vec{v}|^2} = \dfrac{|\vec{a}\times\vec{v}|}{|\vec{v}|^3}$

A partir de la ecuación diferencial 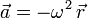$\vec{a} = -\omega^2\,\vec{r}$ . Sabiendo que el módulo de la velocidad es constante e igual a $v 0$ tenemos

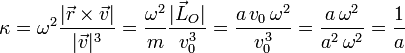
$\kappa = \omega^2\dfrac{|\vec{r}\times\vec{v}|}{|\vec{v}|^3} = \dfrac{\omega^2}{m} \dfrac{|\vec{L}_O|}{v_0^3} = \dfrac{a\,v_0\,\omega^2}{v_0^3} = \dfrac{a\,\omega^2}{a^2\,\omega^2} = \dfrac{1}{a}$

2.2.3 A partir de la trayectoria

La respuesta puede obtenerse de manera aún más rápida si a partir del vector de posición observamos que la trayectoria es una circunferencia. En efecto, en el caso del enunciado tenemos

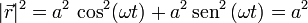
$|\vec{r}|^2 = a^2\,\cos^2(\omega t) + a^2\,\mathrm{sen}^2\,(\omega t) = a^2$

Una curva plana cuyos puntos están todos a la misma distancia del origen es una circunferencia. La curvatura de una circunferencia es constante e igual a la inversa de su radio.

$\kappa = \dfrac{1}{a}$

Muelle sobre un plano horizontal Primera Prueba de Control (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Velocidad areolar

2.2 Curvatura si $v_0=a\,\omega$

2.2.1 Cálculo directo

2.2.2 Usando el momento angular

2.2.3 A partir de la trayectoria

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES