Movimientos Planos de Manivela y Disco, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

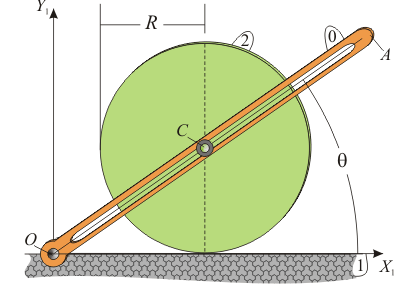
El sistema de la figura está constituido por un plano vertical fijo

O X 1 Y 1

(sólido “1”) que en todo instante contiene a otros dos sólidos en movimiento: un disco de radio

R

y centro

C

(sólido “2”), que rueda sin deslizar sobre el eje horizontal

O X 1

, y una manivela ranurada

O A

(sólido “0”) que es obligada a girar con velocidad angular constante

ω

alrededor de un eje permanente de rotación que pasa por el punto

O

y es perpendicular al plano fijo definido como sólido “1” (eje

O Z 1

). Los movimientos de ambos sólidos se hayan vinculados entre sí porque el centro

C

del disco está obligado a deslizar en todo instante a lo largo de la ranura de la manivela. Considerando el movimiento

{20}

como el movimiento problema, se pide:

Determinar el C.I.R. de dicho movimiento ( $I 20$ ), haciendo uso de procedimientos graficos.
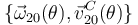Utilizando como parámetro geométrico el ángulo $θ$ indicado en la figura, obtener la reducción cinemática del movimiento ${20}$ en el punto $C$ , $\{\vec{\omega}_{20} (\theta), \vec{v}_{20}^C (\theta)\}$ .
Caracterizar el movimiento ${20}$ en el instante en que $θ = π / 2$ , indicando de forma razonada si se trata de una situación de: (a) rotación instantánea; (b) traslación instantánea; (c) movimiento helicoidal tangente, o (d) reposo instantáneo.

2 Solución

Antes de pasar a resolver las cuestiones propuestas en este ejercicio de movimientos planos relativos de sólidos rígidos, resulta conveniente proceder a la definición de los sistemas de referencia que asociaremos a cada uno de los sólidos. El disco de radio $R$ y centro $C$ (sólido “2”) y la barra $O A$ (sólido “0”), realizan sendos movimientos planos respecto del plano fijo $O X 1 Y 1$ en el cuál van a estar contenidos en todo instante y que, por tanto, adoptaremos como plano director de los movimientos. Tomamos como eje $O Y 1$ la dirección perpendicular a la superficie fija (sólido “1”) sobre la que rueda sin deslizar el disco y en la cual se halla articulada la barra $O A$ en su extremo $O$ .

Los sólidos “0” y “2” tendrán asociados sendos sistemas de referencia $O X 0 Y 0 Z 0$ y $C X 2 Y 2 Z 2$ , tales que,

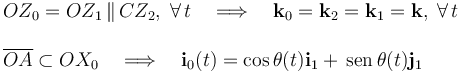
$\begin{array}{l}OZ_0=OZ_1\!\ \|\!\ CZ_2\mathrm{,}\,\;\forall\, t\quad \Longrightarrow\quad\mathbf{k}_0=\mathbf{k}_2=\mathbf{k}_1=\mathbf{k}\mathrm{,}\,\;\forall\, t\\ \\ \overline{OA}\subset OX_0\quad\Longrightarrow\quad \mathbf{i}_0(t)=\cos\theta(t)\mathbf{i}_1+\,\mathrm{sen}\,\theta (t)\mathbf{j}_1\end{array}$

En cuanto al sólido “2”, su simetría en torno al eje $C Z 2$ permite tomar como ejes $C X 2$ y $C Y 2$ dos direcciones cualesquiera contenidas en el plano del disco y perpendiculares entre sí.

En cualquiera de los posibles movimientos relativos ${i j}$ (sólido “ $i$ ” respecto del “ $j$ ”), se tendrá que la dirección del correspondiente vector rotación instantánea es constante:

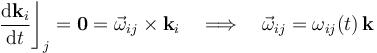
$\frac{\mathrm{d}\mathbf{k}_i}{\mathrm{d}t}\bigg\rfloor_j=\mathbf{0}=\vec{\omega}_{ij}\times\mathbf{k}_i\quad\Longrightarrow\quad\vec{\omega}_{ij}=\omega_{ij}(t)\!\ \mathbf{k}$

Por otra parte, el disco y la barra $O A$ se pueden mover, pero siempre contenidas en el plano $O X 1 Y 1$ . En consecuencia, la velocidad de cualquier punto en cualquiera de los posibles ${i j}$ va a ser un vector paralelo a dicho plano y, por tanto, perpendicular a la dirección definida por el unitario constante 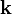$\mathbf{k}$ . Se tendrá, por tanto, que los elementos de las reducciones cinemáticas de cualquiera de los movimientos relativos instantáneos verifican las características del movimiento plano:

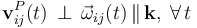
$\mathbf{v}_{ij}^P(t)\!\ \perp\!\ \vec{\omega}_{ij}(t)\!\ \|\!\ \mathbf{k}\mathrm{,}\,\;\forall\, t$

Si el vector rotación es no nulo, va a haber un punto $I$ contenido en el plano director que, en el movimiento ${i j}$ , tiene velocidad nula. Este punto se denomina centro instantáneo de rotación (C.I.R.) del movimiento (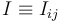 $I\equiv I_{ij}$ ). Entonces, para todo punto $P$ que se mueve solidariamente con el sólido “1”, se tendrá que:

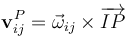
$\mathbf{v}_{ij}^P=\vec{\omega}_{ij}\times\overrightarrow{IP}$

En el caso de una traslación instantánea en que todos los puntos tienen igual vector velocidad y el vector rotación es nulo, la anterior expresión matemática sigue siendo válida si se considera que el C.I.R. se encuentra en el infinito, en la dirección paralela al plano director y perpendicular a la de las velocidades instantáneas.

2.1 Posición de los C.I.R. de los tres movimientos relativos

El extremo

O

del sólido “0” está articulado en el punto fijo

O

del sólido “1”. Por tanto, dicho punto se encuentra en reposo permanente en el movimiento

{01}

que se produce cuando la barra

O A

(sólido “0”) gira alredor del eje

O Z 1

. En consecuencia, y de acuerdo con la exposición anterior, el punto

O

será el centro de rotación permanente del movimiento

{01}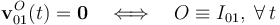

: $\mathbf{v}_{01}^O(t)=\mathbf{0}\quad\Longleftrightarrow\quad O\equiv I_{01}\mathrm{,}\,\;\forall\,t$

El disco rueda sin deslizar sobre la superficie que hemos definido como sólido “1”. En consecuencia, el punto del sólido “2” que en cada instante se haya en contacto con el eje $O X 1$ , se encuentra en estado de reposo instantáneo. Si en todo instante denotamos como punto $B$ dicha posición de contacto, se tendrá que:

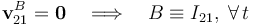
$\mathbf{v}_{21}^B=\mathbf{0}\quad\Longrightarrow\quad B\equiv I_{21}\mathrm{,}\,\;\forall\,t$

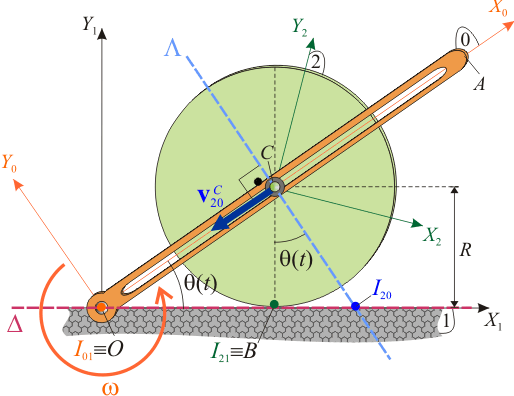
Es decir, en cada instante de tiempo el C.I.R. del movimiento ${21}$ se encuentra en el punto $B$ de contacto entre el disco y la superficie fija. Obsérvese que la posición de dicho punto va cambiando durante el transcurso del movimiento, sin embargo, siempre va a estar en el eje sobre el eje $O X 1$ . Por tanto, los C.I.R. $I 21$ e $I 01$ definen en todo instante una recta $Δ$ que coincide con el eje $O X 1$ . En virtud del teorema de los tres centros, el C.I.R. del movimiento ${20}$ van a estar alineado en cada instante con los de los movimientos ${01}$ y ${21}$ . En consecuencia, el $I 20$ debe encontrarse siempre sobre la recta $Δ$ definida por $O$ y $B$ en cada instante:

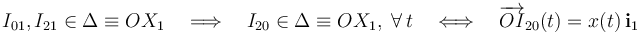
$I_{01}\mathrm{,}\!\ I_{21}\in\Delta\equiv OX_1\quad\Longrightarrow\quad I_{20}\in\Delta\equiv OX_1\mathrm{,}\;\,\forall\,t\quad\Longleftrightarrow\quad \overrightarrow{OI}_{20}(t)=x(t)\!\ \mathbf{i}_1$

Por otra parte, la expresión del campo de velocidades del movimiento ${20}$ indica que la posición del C.I.R. $I 20$ , respecto de un punto arbitrario $P$ , se encuentra en la dirección perpendicular a la velocidad del punto en dicho movimiento

$\mathbf{v}_{20}^P=\vec{\omega}_{20}\times\overrightarrow{I_{20}P}\quad\Longrightarrow\quad \overrightarrow{PI}_{20}\!\ \perp \!\ \mathbf{v}_{20}^P\mathrm{,}\!\ \mathbf{k}$

Hay un punto concreto del disco para el cuál conocemos el todo instante la dirección de su velocidad en el movimiento ${20}$ : el centro $C$ del disco está obligado a desplazarse siempre a lo largo del carril practicado a lo largo de la barra $O A$ , que coincide con la dirección $O X 0$ , de manera que:

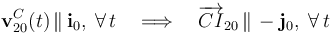
$\mathbf{v}_{20}^C(t)\!\ \|\!\ \mathbf{i}_0\mathrm{,}\;\,\forall\,t\quad\Longrightarrow\quad \overrightarrow{CI}_{20}\!\ \|\!\ -\mathbf{j}_0\mathrm{,}\;\,\forall\,t$

En consecuencia, el C.I.R. del movimiento ${20}$ se encuentra en cada instante en la recta que pasa por el centro $C$ del disco y es paralela a la dirección del eje $O Y 0$ (perpendicular a $O A$ ):

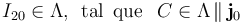
$I_{20}\in\Lambda\mathrm{,}\,\;\,\mathrm{tal}\;\,\mathrm{que}\,\;\; C\in\Lambda\!\ \|\!\ \mathbf{j}_0$

Así que, en cada instante, el C.I.R. del movimiento ${20}$ se halla en la intersección de las rectas $Δ$ y $Λ$ ; es decir, donde la recta que pasa por el centro del disco y es perpendicular a la barra, corta al eje $O X 1$ :

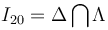
$I_{20}=\Delta\bigcap\Lambda$

La descripción analítica de dicho punto respecto del origen $O$ de los sistemas de referencia asociados a los sólidos “1” y “0” se puede obtener sin más que tener en cuenta que, en todo instante, los puntos $O$ , $C$ e $I 20$ son los vértices de un triángulo rectángulo cuyo ángulo recto se encuentra en el vértice $C$ . Por tanto,

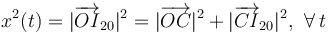
$x^2(t)=|\overrightarrow{OI}_{20}|^2=|\overrightarrow{OC}|^2+|\overrightarrow{CI}_{20}|^2\mathrm{,}\;\;\forall\,t$

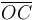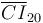Las longitudes de los segmentos $\overline{OC}$ y $\overline{CI}_{20}$ pueden expresarse en cada instante en función del ángulo $θ$ que forman con las direcciones horizontal y vertical, respectivamente. Teniendo en cuenta que la distancia entre el centro $C$ del disco y el punto de contacto $B$ es siempre constante e igual al radio del disco, se obtiene:

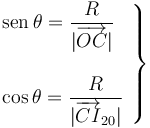
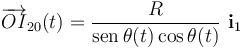
$\left.\begin{array}{l}\displaystyle\mathrm{sen}\,\theta=\frac{R}{|\overrightarrow{OC}|}\\ \\ \displaystyle\cos\theta=\frac{R}{|\overrightarrow{CI}_{20}|}\end{array}\right\}$ $\Rightarrow$ $\overrightarrow{OI}_{20}(t)=\frac{R}{\mathrm{sen}\,\theta(t)\cos\theta(t)}\ \mathbf{i}_1$

2.2 Reducción cinemática del movimiento ${20}$

Para determinar la reducción cinemática instantánea de este movimiento, podemos seguir dos procedimientos distintos: el análisis directo de dicho movimiento relativo en cada instante, o la aplicación de la composición de movimientos relativos.

2.2.1 Análisis cinemático directo

El centro del disco (sólido ``2") está obligado a desplazarse por la barra $O A$ (sólido ``1"), que coincide en todo instante con el eje $O X 0$ . Se tendrá,por tanto que:

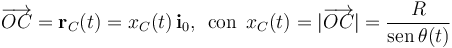
$\overrightarrow{OC}=\mathbf{r}_C(t)=x_C(t)\!\ \mathbf{i}_0\mathrm{,}\,\;\,\mathrm{con}\,\;x_C(t)=|\overrightarrow{OC}|=\frac{R}{\mathrm{sen}\,\theta(t)}$

ya que 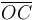$\overline{OC}$ es la hipotenusa del triángulo rectángulo que en cada instante tiene por vértices los puntos $O$ , $B$ y $C$ . La expresión de la velocidad instántánea del punto $C$ en el movimiento ${20}$ se obtiene derivando con respecto al tiempo el anterior vector posición, en el sistema de referencia $O X 0 Y 0 Z 0$ :

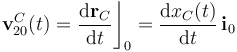
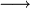
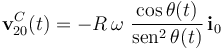
$\mathbf{v}_{20}^C(t)=\frac{\mathrm{d}\mathbf{r}_C}{\mathrm{d}t}\bigg\rfloor_0=\frac{\mathrm{d}x_C(t)}{\mathrm{d}t}\!\ \mathbf{i}_0$ $\longrightarrow$ $\mathbf{v}_{20}^C(t)=-R\!\ \omega\ \frac{\cos\theta(t)}{\mathrm{sen}^2\,\theta (t)}\!\ \mathbf{i}_0$

donde se ha tenido en cuenta que la velocidad angular de rotación $ω$ de la barra, respecto de los ejes fijos es, por definición, la variación instantánea del ángulo $θ$ , por unidad de tiempo:

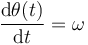
$\frac{\mathrm{d}\theta(t)}{\mathrm{d}t}=\omega$

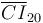Una vez determinada la expresión de la velocidad instantánea de $C$ , pordemos obtener el otro elemento de la reducción (es decir, el vector rotación $\vec{\omega}_{20}$ ) aprovechando que conocemos en cada instante la posición del C.I.R. del movimiento ${20}$ . En el apartado anterior se determinó la dirección módulo y sentido del vector $\overline{CI}_{20}$ :

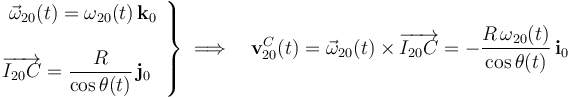
$\left.\begin{array}{l}\ \vec{\omega}_{20}(t)=\omega_{20}(t)\!\ \mathbf{k}_0\\ \\ \displaystyle\overrightarrow{I_{20}C}=\frac{R}{\cos\theta(t)}\!\ \mathbf{j}_0\end{array}\right\}\;\Longrightarrow\quad \mathbf{v}_{20}^C(t)=\vec{\omega}_{20}(t)\times\overrightarrow{I_{20}C}=-\frac{R\!\ \omega_{20}(t)}{\cos\theta(t)}\!\ \mathbf{i}_0$

Igualandon esta expresión con la obtenida por derivación del vector posición se obtiene,

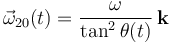
$\vec{\omega}_{20}(t)= \frac{\omega}{\mathrm{tan}^2\,\theta (t)}\!\ \mathbf{k}$

2.2.2 Composición de movimientos relativos

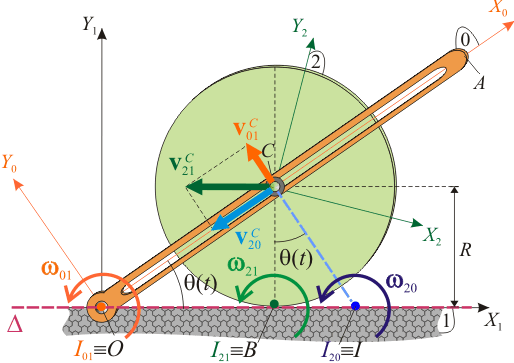
En este caso, necesitamos conocer las reducciones cinemáticas de los tres movimientos relativos en un instante arbitrario

t

, en el cuál la posición del sistema viene dada por un valor

θ

del ángulo que forman la barra

O A

y la dirección fija

O X 1

. Como conocemos las posiciones de los C.I.R. de los tres movimientos, utilizaremos las correspondientes reducciones canónicas:

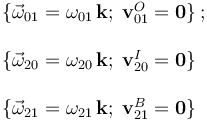
$\begin{array}{l}\{\vec{\omega}_{01}=\omega_{01}\!\ \mathbf{k}\mathrm{;}\,\;\mathbf{v}_{01}^O=\mathbf{0}\}\,\mathrm{;}\\ \\ \{\vec{\omega}_{20}=\omega_{20}\!\ \mathbf{k}\mathrm{;}\,\; \mathbf{v}_{20}^I=\mathbf{0}\}\\ \\ \{\vec{\omega}_{21}=\omega_{21}\!\ \mathbf{k}\mathrm{;}\,\;\mathbf{v}_{21}^B=\mathbf{0}\}\end{array}$

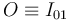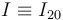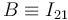donde $O\equiv I_{01}$ ; $I\equiv I_{20}$ , y $B\equiv I_{21}$ son las posiciones que ocupan los C.I.R. en el instante arbitrario considerado. En cuanto a las componentes de los vectores rotación instantánea, sólo podemos conocer a priori el valor de $ω 01$ . De las fórmulas de Poisson se obtiene:

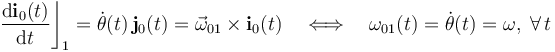
$\frac{\mathrm{d}\mathbf{i}_0(t)}{\mathrm{d}t}\bigg\rfloor_1=\dot{\theta}(t)\!\ \mathbf{j}_0(t)=\vec{\omega}_{01}\times\mathbf{i}_0(t)\quad\Longleftrightarrow\quad \omega_{01}(t)=\dot{\theta}(t)=\omega\mathrm{,}\,\;\forall\, t$

Calculamos ahora las velocidades instantáneas del punto $C$ en cada uno de los movimientos relativos:

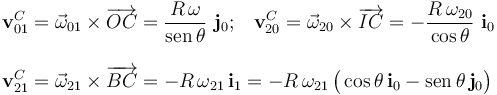
$\begin{array}{l}\displaystyle\mathbf{v}_{01}^C=\vec{\omega}_{01}\times\overrightarrow{OC}=\frac{R\!\ \omega}{\mathrm{sen}\,\theta}\ \mathbf{j}_0\mathrm{;}\quad \displaystyle\mathbf{v}_{20}^C=\vec{\omega}_{20}\times\overrightarrow{IC}=-\frac{R\!\ \omega_{20}}{\mathrm{cos}\,\theta}\ \mathbf{i}_0\\ \\ \displaystyle\mathbf{v}_{21}^C=\vec{\omega}_{21}\times\overrightarrow{BC}=-R\!\ \omega_{21}\!\ \mathbf{i}_1=-R\!\ \omega_{21}\!\ \big(\cos\theta\!\ \mathbf{i}_0-\mathrm{sen}\,\theta\!\ \mathbf{j}_0\big)\end{array}$

La ley de composición de velocidades instantáneas establece que...

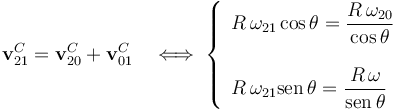
$\mathbf{v}_{21}^C=\mathbf{v}_{20}^C+\mathbf{v}_{01}^C\quad\Longleftrightarrow\;\left\{\begin{array}{l} \displaystyle R\!\ \omega_{21}\cos\theta=\frac{R\!\ \omega_{20}}{\cos\theta}\\ \\ \displaystyle R\!\ \omega_{21}\mathrm{sen}\,\theta=\frac{R\!\ \omega}{\mathrm{sen}\,\theta}\end{array}\right.$

Teniendo en cuenta que estas relaciones deben cumplirse en cada instante $t$ , cuando el parámetro geométrico que describe la posición en dicho instante vale $θ(t)$ , se obtiene:

$\omega_{21} (t)=\frac{\omega}{\mathrm{sen}^2\theta(t)}\quad\Longrightarrow\quad \omega_{20} (t)=\frac{\omega}{\mathrm{tan}^2\theta(t)}$

Y sustityendo este último resultado en las expresiones de 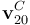$\mathbf{v}_{20}^C$ y $\vec{\omega}_{20}$ , obtenemos la reducción cinemática del movimiento ${20}$ en el centro del disco, y para cualquier instante de tiempo:

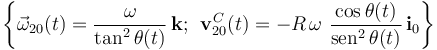
$\left\{\vec{\omega}_{20}(t)= \frac{\omega}{\mathrm{tan}^2\,\theta (t)}\!\ \mathbf{k}\mathrm{;}\,\;\, \mathbf{v}_{20}^C(t)=-R\!\ \omega\ \frac{\cos\theta(t)}{\mathrm{sen}^2\,\theta (t)}\!\ \mathbf{i}_0\right\}$

2.3 Estado cinemático del disco respecto de la manivela en $θ = π / 2$

Consideremos el instante $t 0$ en que la manivela $O A$ está colocado perpendicularmente al eje $O X 1$ sobre el que rueda sin deslizar el disco; es decir,

$OA\!\ \|\!\ OY_1\quad\Longleftrightarrow\quad \theta(t_0)=\frac{\pi}{2}$

En dicho instante, el estado cinemático del disco en su movimiento respecto de la manivela, está completamente determinado por la correspondiente reducción cinemática:

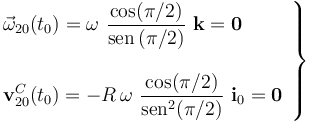
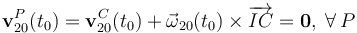
$\left.\begin{array}{l}\displaystyle\vec{\omega}_{20}(t_0)=\omega\ \frac{\cos(\pi/2)}{\mathrm{sen}\,(\pi/2)}\ \mathbf{k}=\mathbf{0}\\ \\ \displaystyle\mathbf{v}_{20}^C(t_0)=-R\!\ \omega\ \frac{\cos(\pi/2)}{\mathrm{sen}^2(\pi/2)}\ \mathbf{i}_0=\mathbf{0}\end{array}\right\}$ $\Rightarrow$ $\mathbf{v}_{20}^P(t_0)=\mathbf{v}_{20}^C(t_0)+\vec{\omega}_{20}(t_0)\times\overrightarrow{IC}=\mathbf{0}\mathrm{,}\,\;\forall\,P$

Luego, en el intante $t 0$ , el disco (sólido ``2") se halla en reposo respecto de la manivela $O A$ (sólido ``0"). Para determinar si se trata de una situación de reposo instantáneo, hay que comprobar si en un instante inmediatamente posterior a $t 0$ alguno de los elementos de la reducción cinemática del movimiento ${20}$ va a ser no nulo. Como sabemos, esto ocurrirá si las derivadas instantáneas de alguno de dichos elementos en el instante $t 0$ es también un vector no nulo. Y puesto que tenemos la ley horaria para el vector rotación instantánea en dicho movimiento, y también para la velocidad instantánea del centro del disco, podemos calcular cualquiera de sus derivadas temporales. Por ejemplo

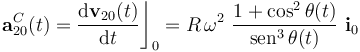
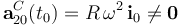
$\mathbf{a}_{20}^C(t)=\frac{\mathrm{d}\mathbf{v}_{20}(t)}{\mathrm{d}t}\bigg\rfloor_0=R\!\ \omega^2\ \frac{1+\cos^2\theta(t)}{\mathrm{sen}^3\,\theta(t)}\ \mathbf{i}_0$ $\Rightarrow$ $\mathbf{a}_{20}^C(t_0)=R\!\ \omega^2\!\ \mathbf{i}_0\neq\mathbf{0}$

Por tanto, en el instante en que la manivela o barra $O A$ forma un ángulo de $π / 2$ con la dirección $O X 1$ , el disco se encuentra en reposo instantáneo respecto de aquélla.

Movimientos Planos de Manivela y Disco, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posición de los C.I.R. de los tres movimientos relativos

2.2 Reducción cinemática del movimiento ${20}$

2.2.1 Análisis cinemático directo

2.2.2 Composición de movimientos relativos

2.3 Estado cinemático del disco respecto de la manivela en $θ = π / 2$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Movimientos Planos de Manivela y Disco, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posición de los C.I.R. de los tres movimientos relativos

2.2 Reducción cinemática del movimiento {20}

2.2.1 Análisis cinemático directo

2.2.2 Composición de movimientos relativos

2.3 Estado cinemático del disco respecto de la manivela en θ = π / 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2 Reducción cinemática del movimiento ${20}$

2.3 Estado cinemático del disco respecto de la manivela en $θ = π / 2$