Movimiento uniforme de partícula describiendo trayectoria tridimensional, F1 GIA (Nov, 2016)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

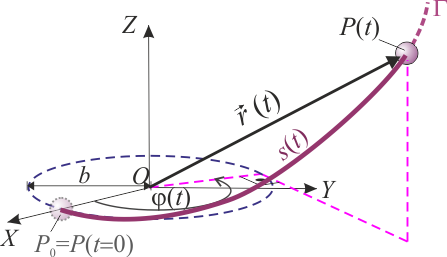
Una partícula $P$ se mueve respecto de un sistema de referencia cartesiano fijo $O X Y Z$ , recorriendo la curva de ecuación paramétrica,

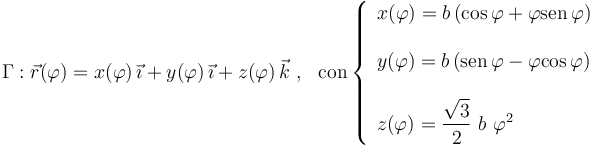
$\Gamma :\vec{r}(\varphi)=x(\varphi)\!\ \vec{\imath}+y(\varphi)\!\ \vec{\imath}+z(\varphi)\!\ \vec{k}\ \mathrm{,}\;\;\; \mathrm{con}\left\{ \begin{array} {l} x(\varphi)= b\!\ (\mathrm{cos}\!\ \varphi +\varphi\mathrm{sen}\!\ \varphi)\\ \\ y(\varphi)= b\!\ (\mathrm{sen}\!\ \varphi -\varphi\mathrm{cos}\!\ \varphi)\\ \\ \displaystyle z(\varphi)=\frac{\sqrt{3}}{2}\ b\ \varphi^2 \end{array}\right.$

donde $b$ es un valor constante conocido, y $\varphi$ un determinado parámetro geométrico. En el instante inicial, $t = 0$ , la partícula se encuentra en el punto de coordenadas $P 0 (b,0,0)$ , en reposo; a partir de dicho instante y posición, realiza un movimiento uniforme con velocidad de módulo constante, $v 0$ .

Ley horaria $\varphi(t)$ que ha de cumplir el parámetro geométrico para que $\vec{r}[\varphi(t)]$ sea el movimiento uniforme descrito en el enunciado.
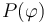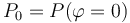Relación entre el valor del parámetro $\varphi$ correspondiente a una posición arbitraria de la partícula, $P(\varphi)$ , y la distancia $s$ , medida sobre la curva, desde dicho punto al punto $P_0=P(\varphi=0)$ .
Vector aceleración instantánea de la partícula en función de la posición de la partícula, dada por el valor del parámetro $\varphi$ en cada instante de tiempo.

2 Solución

2.1 Condición de movimiento uniforme

Para que el movimiento de la partícula sea uniforme, es necesario que su velocidad sea constante. Así, deberemos calcular la expresión de esta magnitud cinemática e imponer dicha condición necesaria. Por tora parte, sabemos que la velocidad instantánea de la partícula es igual a la derivada con respecto al tiempo de las ecuaciones horarias, que describen la posición de la partícula respecto de un sistema de referencia, en términos de un vector posición expresado como una función vectorial de la posición. En este caso, dichas ecuaciones horarias vendrán dadas por la composición de la ecuación parámetrica de la trayectoria, 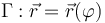$\Gamma: \vec{r}=\vec{r}(\varphi)$ (que es una función conocida del parámetro geométrico $\varphi$ ), y la ley horaria $\varphi(t)$ (desconocida), que en cada instante de tiempo permitiría determinar la posición de la partícula en la trayectoria. Por tanto, la derivada instantánea de dicha magnitud (la velocidad), puede obtenerse mediante la apliación de la regla de la cadena:

$\left.\begin{array}{r}\forall\, t\mathrm{,}\;\; P\in \Gamma: \vec{r}=\vec{r}(\varphi)\\ \\ \varphi=\varphi(t)\end{array}\right\}\;\longrightarrow\;\overrightarrow{OP}=\vec{r}[\varphi(t)]=\vec{r}(t)\quad \;\Longrightarrow\;\quad \vec{v}(t)=\frac{\mathrm{d}\vec{r}(t)}{\mathrm{d}t}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}\varphi}\ \frac{\mathrm{d}\varphi}{\mathrm{d}t}$

Obsérvese que el primer factor (la primera de las derivadas) puede ser calculada a partir de los datos de la trayectoria...

$\displaystyle \frac{\mathrm{d}\vec{r}}{\mathrm{d}\varphi}=\frac{\mathrm{d}x(\varphi)}{\mathrm{d}\varphi}\ \vec{\imath}+\frac{\mathrm{d}y(\varphi)}{\mathrm{d}\varphi}\ \vec{\jmath}+\frac{\mathrm{d}z(\varphi)}{\mathrm{d}\varphi}\ \vec{k}= b\!\ \varphi \!\ \bigg[ \mathrm{cos}\!\ \varphi\!\ \vec{\imath}+ \mathrm{sen}\!\ \varphi\!\ \vec{\jmath}+\sqrt{3}\!\ \vec{k}\bigg]$

Sin embargo, el segundo factor será una función del tiempo desconocida a priori,

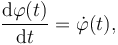
$\frac{\mathrm{d}\varphi(t)}{\mathrm{d}t}=\dot{\varphi}(t)\mathrm{,}\;\;$

pues desconocemos la ley horaria $\varphi (t)$ que describe el movimiento de la partícula sobre la trayectoria. No obstante, podemos concluir que el vector velocidad instantánea será de la forma:

$\vec{v}(t)=\frac{\mathrm{d}\vec{r}}{\mathrm{d}\varphi}\ \frac{\mathrm{d}\varphi}{\mathrm{d}t}=b\!\ \varphi \!\ \dot{\varphi}(t)\!\ \bigg[ \mathrm{cos}\!\ \varphi\!\ \vec{\imath}+ \mathrm{sen}\!\ \varphi\!\ \vec{\jmath}+\sqrt{3}\!\ \vec{k}\bigg]$

Para obtener cómo es dicha ley horaria, imponemos la condición expresada en el enunciado de que el movimiento que realiza la partícula a lo largo de la trayectoria ha de ser un movimiento uniforme, caracterizado porque la velocidad tiene módulo constante de valor conocido $v 0$ en todo instante. Por tanto, ha de cumplirse...

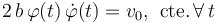
$\left.\begin{array}{r} \displaystyle |\vec{v}(t)|=v_0\mathrm{,}\;\;\mathrm{cte.}\,\forall\, t\\ \\ |\vec{v}(t)|^2=\vec{v}\cdot\vec{v}= \left[b\!\ \varphi (t) \!\ \dot{\varphi} (t)\right]^2\ \bigg[\mathrm{cos}^2\!\ \varphi (t) + \mathrm{sen}^2\!\ \varphi (t) + 3\bigg]=4\!\ \left[b\!\ \varphi (t) \!\ \dot{\varphi} (t)\right]^2\end{array}\right\}\;\Longrightarrow\;$ $2\!\ b\!\ \varphi (t)\!\ \dot{\varphi}(t)=v_0\mathrm{,}\;\;\mathrm{cte.}\,\forall\, t$

... es la ecuación diferencial que ha de verificar en todo instante la ley horaria $\varphi (t)$ . Este resultado implica la hipotesis de que el producto de la función $\varphi (t)$ por su derivada ha de ser siempre una cantidad positiva. Por otra parte, obsérvese que la solución de dicha ecuación es inmediata si se tiene en cuenta que dada una función del tiempo $f = f (t)$ , se cumplirá que

$\frac{\mathrm{d}}{\mathrm{d}t}\bigg[f^2(t)\bigg]=2\!\ f(t)\!\ \frac{\mathrm{d}f(t)}{\mathrm{d}t}$

En consecuencia, se tendrá que la ecuación diferencial para $\varphi (t)$ puede reformularse de la siguiente manera:

$2\!\ \varphi (t)\!\ \dot{\varphi}(t)=\frac{\mathrm{d}}{\mathrm{d}t}\bigg[\varphi^2(t)\bigg] =\frac{v_0}{b}\mathrm{,}\;\;\mathrm{cte.}\,\forall\, t\;\;\; \Longrightarrow\;\;\;\varphi^2 (t)=\frac{v_0}{b}\ t + K$

donde $K$ es una constante a determinar, a partir de las condiciones iniciales del problema. Para ello, utilizamos el dato que en el instante inicial, $t = 0$ , la partícula se encuentra en la posición $P 0 (b,0,0)$ . Es decir, en dicho instante, la partícula se encuentra en el plano $O X Y$ , por tanto:

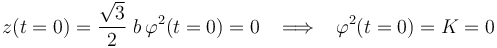
$z(t=0)=\frac{\sqrt{3}}{2}\ b \!\ \varphi^2(t=0)=0\;\; \; \Longrightarrow \;\;\; \varphi^2(t=0)=K=0$

Una vez determinada la constante, la solución para la ley horaria del parámetro geométrico $\varphi$ , que describe el movimiento uniforme de la partícula en la trayectoria descrita es:

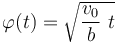
$\varphi (t)=\sqrt{\frac{v_0}{b}\ t}$

2.1.1 Expresiones cartesiana e intrínseca de la velocidad

Una vez determinada la ley horaria para el parámetro geométrico $\varphi (t)$ y, teniendo en cuenta que la celeridad es constante, se tendrá que la expresión analítica del vector velocidad instantánea en el sistema de coordenadas cartesianas es:

$\vec{v}(t)=\frac{v_0}{2}\ \left[ \mathrm{cos}\!\ \varphi (t)\!\ \vec{\imath}+ \mathrm{sen}\!\ \varphi (t)\!\ \vec{\jmath}+\sqrt{3}\!\ \vec{k}\right]=\vec{v}[\varphi(t)]\mathrm{,}\;\;\mathrm{con}\;\;\; \varphi(t)=\sqrt{\frac{v_0}{b}\ t}$

Por otra parte, la expresión intrínseca de la velocidad es inmediata:

$\vec{v}(t)=v(t)\!\ \vec{T}[\varphi(t)]\mathrm{,}\;\;\mathrm{con}\quad\left\{\begin{array}{l} v(t)=|\vec{v}(t)|=v_0\mathrm{,}\;\;\mathrm{cte.}\;\;\;\forall\,t\\ \\ \displaystyle \vec{T}[\varphi(t)]=\frac{\vec{v}(t)}{|\vec{v}(t)|}=\frac{1}{2}\ \left[ \mathrm{cos}\!\ \varphi (t)\!\ \vec{\imath}+ \mathrm{sen}\!\ \varphi (t)\!\ \vec{\jmath}+\sqrt{3}\!\ \vec{k}\right] \end{array}\right.$

siendo $\vec{T}[\varphi(t)]$ el vector unitario tangente a la trayectoria de la partícula en la posición que esta ocupa en el instante arbitrario $t$ .

2.2 Relación del parámetro geométrico con el parámetro arco

En el sistema bajo estudio, la partícula realiza un movimiento uniforme con velocidad de módulo constante de valor conocido $v 0$ . En este caso, la ley horaria $s = s (t)$ para la distancia recorrida por la partícula a lo largo de la trayectoria (parámetro arco), es muy simple. Como se sabe, la derivada temporal de dicha ley horaria es igual a la celeridad o módulo de la velocidad. Si además tenemos en cuenta que se empiezan a medir distancias sobre la trayectoria a partir de la posición correspondiente al instante inicial $t = 0$ , se tendrá:

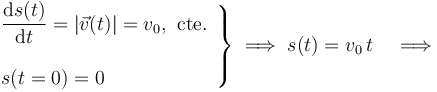
$\left.\begin{array}{l}\displaystyle \frac{\mathrm{d}s(t)}{\mathrm{d}t}=|\vec{v}(t)|=v_0\mathrm{,}\;\;\mathrm{cte.} \\ \\ s(t=0)=0 \end{array}\right\}\; \Longrightarrow \;s(t)=v_0\!\ t\; \;\;\;\Longrightarrow$ $\varphi [s(t)]=\sqrt{\frac{s(t)}{b}}$

2.3 Aceleración instantánea de la partícula

La aceleración instantánea de la partícula, 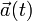$\vec{a}(t)$ , es el vector que describe como cambia en cada instante, y por unidad de tiempo, el vector velocidad instantánea y, como sabemos, puede calcularse como la derivada con respecto a tiempo de dicho vector velocidad. Aplicando de nuevo la regla de la cadena...

$\vec{a}(t)=\frac{\mathrm{d}\vec{v}(t)}{\mathrm{d}t}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}\varphi}\ \frac{\mathrm{d}\varphi}{\mathrm{d}t}=\dot{\varphi}(t)\!\ \frac{v_0}{2}\ \bigg[ -\mathrm{sen}\!\ \varphi (t)\!\ \vec{\imath}+ \mathrm{cos}\!\ \varphi (t)\!\ \vec{\jmath}\!\ \bigg]\mathrm{,}\;\;\mathrm{con}\;\;\; \varphi(t)=\sqrt{\frac{v_0}{b}\ t}$

Aplicando la ecuación diferencial para la ley horaria $\varphi (t)$ ...

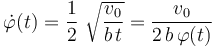
$\dot{\varphi}(t)=\frac{1}{2}\ \sqrt{\frac{v_0}{b\!\ t}}=\frac{v_0}{2\!\ b\!\ \varphi (t)}$

... y sustituyendo en la expresión de la aceleración instantánea, se obtiene:

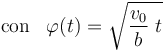
$\vec{a}(t)=\frac{\mathrm{d}\vec{v}(t)}{\mathrm{d}t}= \frac{v_0^2}{4\!\ b\!\ \varphi (t)}\ \bigg[ -\mathrm{sen}\!\ \varphi (t)\!\ \vec{\imath}+ \mathrm{cos}\!\ \varphi (t)\!\ \vec{\jmath}\!\ \bigg]=\vec{a}[\varphi(t)]\mathrm{,}$ $\mathrm{con}\;\;\; \varphi(t)=\sqrt{\frac{v_0}{b}\ t}$

2.3.1 Expresión intrínseca de la aceleración

La expresión de la aceleración instantánea en términos de las coordenadas intrínsecas es...

$\vec{a}[\varphi(t)]=\frac{v_0^2}{4\!\ b\!\ \varphi (t)}\ \bigg[ -\mathrm{sen}\!\ \varphi (t)\!\ \vec{\imath}+ \mathrm{cos}\!\ \varphi (t)\!\ \vec{\jmath}\!\ \bigg]=a_T(t)\!\ \vec{T}[\varphi(t)]+a_N(t)\!\ \vec{N}[\varphi(t)]$

donde $\vec{T}[\varphi(t)]$ y $\vec{N}[\varphi(t)]$ son los vectores unitarios en las direcciones tangente y normal a la trayectoria en la posición ocupada por la partícula en el instante $t$ . Por su parte, la componente tangencial de la aceleración es nula en todo instante, ya la velocidad tiene módulo constante. Por tanto, la aceleración sólo tendrá componente normal:

$a_T(t)=\frac{\mathrm{d}v(t)}{\mathrm{d}t}=0\mathrm{,}\;\;\forall\, t \;\; \Longrightarrow \;\; \vec{a}(t)]=a_N(t)\!\ \vec{N}[\varphi(t)]\mathrm{,}\;\; \mathrm{con}\;\;\; \left\{\begin{array}{l} \displaystyle a_N [\varphi (t)]= \frac{v_0^2}{4\!\ b\!\ \varphi (t)}=\frac{v_0^{3/2}}{4\!\ (b\!\ t)^{1/2}}\\ \\ \displaystyle \vec{N}[\varphi(t)]= -\mathrm{sen}\!\ \varphi (t)\!\ \vec{\imath}+ \mathrm{cos}\!\ \varphi (t)\!\ \vec{\jmath}\end{array}\right.$

Por otra parte, la componente normal de la aceleración nos permite determinar el radio de curvatura de la trayectoria 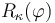$R_\kappa (\varphi)$ en función de la posición de la partícula:

$a_N[\varphi(t)]=\frac{v_0^2}{4\!\ b\!\ \varphi (t)}=\frac{v^2(t)}{R_\kappa [\varphi(t)]}\;\;\; \Longrightarrow \;\;\; R_\kappa [\varphi(t)]=4\!\ b\!\ \varphi (t)$

Movimiento uniforme de partícula describiendo trayectoria tridimensional, F1 GIA (Nov, 2016)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Condición de movimiento uniforme

2.1.1 Expresiones cartesiana e intrínseca de la velocidad

2.2 Relación del parámetro geométrico con el parámetro arco

2.3 Aceleración instantánea de la partícula

2.3.1 Expresión intrínseca de la aceleración

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES