Movimiento de una partícula por acción de la gravedad (GIOI)

De Laplace

Contenido

1 Gravedad y peso
2 Movimiento en las proximidades de la Tierra
- 2.1 Sin rozamiento con el aire
- 2.2 En presencia de rozamiento
3 Movimiento orbital. Ley de la Gravitación Universal
4 La tercera ley de Kepler
5 Gravedad y geometría

1 Gravedad y peso

Que los objetos caen por acción de la gravedad es una evidencia conocida desde tiempo inmemorial. Sin embargo, la expresión matemática de la caída de los cuerpos, requirió un proceso intelectual elaborado, por las dificultades de aislar el efecto de la gravedad frente a otros. Consideremos el caso de la caída de los cuerpos.

Aristóteles afirmó que los cuerpos tienden a su lugar natural y por eso las piedras caen y las burbujas suben. Este modelo fracasa cuando se observa que la gravedad actúa sobre todos los cuerpos por igual y por eso esta teoría debe ser abandonada.

Galileo establece que, en ausencia de rozamiento, todos los cuerpos caen con la misma aceleración

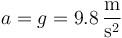
$a= g= 9.8\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Este modelo es válido si queremos estudiar el movimiento de un proyectil a corta distancia o la caída de los cuerpos (en primera aproximación, ya que siempre hay rozamiento con el aire). Esta teoría fue comprobada de manera espectacular en 1971 por los astronautas del Apolo 15 que en la Luna hicieron el experimento de dejar caer a la vez un martillo y una pluma.

Falla si hablamos de un misil balístico intercontinental o el movimiento planetario. Por tanto, aunque el modelo de gravedad constante es aplicable cerca de la superficie terrestre, tiene unos límites de validez en unos decenas o centenares de kilómetros.

Newton extendió el trabajo de Galileo al movimiento planetario, elaborando su ley de la Gravitación Universal

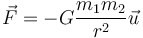
$\vec{F}=-G\frac{m_1m_2}{r^2}\vec{u}$

Usando esta ley, Newton predijo correctamente tanto el comportamiento de la manzana (donde vale la teoría galileana) como el de la Luna, el Sistema Solar. Estas leyes permiten diseñar las misiones interplanetarias

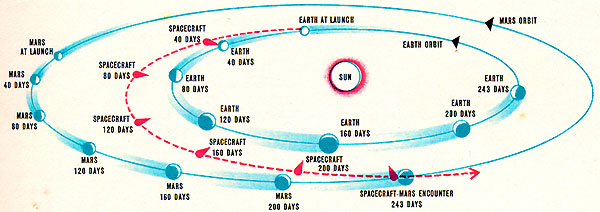
No obstante, la teoría de Newton fallaba a la hora de analizar en detalle la órbita de Mercurio, por lo que sus límites de validez los establece el que los campos gravitatorios no sean demasiado intensos.

Einstein reformuló la teoría newtoniana en su Teoría de la Relatividad General. Interpretando la gravedad como geometría llegó a las llamadas ecuaciones de campo de Einstein

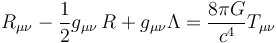
$R_{\mu \nu} - {1 \over 2}g_{\mu \nu}\,R + g_{\mu \nu} \Lambda = {8 \pi G \over c^4} T_{\mu \nu}$

Estas ecuaciones contienen tanto los resultados de Galileo como los de Newton, pero al precio de una complejidad mucho mayor. Las ecuaciones de Einstein son necesarias en algunas aplicaciones que requieren una gran precisión como las sincronizaciones de los satélites del sistema GPS.

Aun así no son universalmente válidas. Se sabe que no son aplicables a objetos extremadamente pequeños, como puede ser el centro de un agujero negro.

2 Movimiento en las proximidades de la Tierra

2.1 Sin rozamiento con el aire

Para una partícula situada en las proximidades de la superficie terrestre podemos suponer que el campo gravitatorio es prácticamente constante y, en ausencia de rozamiento, se mueve con una aceleración común a todos los cuerpos

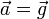
$\vec{a}=\vec{g}$

El resultado de esta aceleración constante es conocido: la partícula describe un movimiento parabólico

ya que la integración de las ecuaciones de movimiento es inmediata. De la aceleración

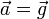
$\vec{a}=\vec{g}$

resulta la velocidad

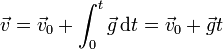
$\vec{v}=\vec{v}_0+\int_0^t \vec{g}\,\mathrm{d}t = \vec{v}_0 + \vec{g}t$

y de aquí la posición

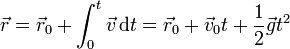
$\vec{r}=\vec{r}_0+\int_0^t \vec{v}\,\mathrm{d}t = \vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{g}t^2$

Separando en componentes quedan las ecuaciones horarias

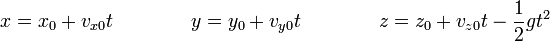
$x = x_0 + v_{x0}t\qquad\qquad y = y_0 + v_{y0}t\qquad\qquad z = z_0 + v_{z0}t-\frac{1}{2}gt^2$

Vemos que la coordenada vertical sigue un movimiento uniformemente acelerado, mientras que las horizontales varían uniformemente.

El que la aceleración sea la misma para todos los cuerpos tiene profundas consecuencias teóricas. De acuerdo con la segunda ley de Newton, sobre cada partícula actúa una fuerza, el peso, dada por

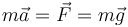
$m\vec{a}=\vec{F}=m\vec{g}$

Ahora bien, la masa que acompaña a la aceleración no es la misma que la que acompaña a la gravedad, aunque lo parezcan (las dos son m, ¿no?). Para ver la distinción, consideremos el caso de una partícula en un campo eléctrico. En este caso la segunda ley de Newton queda

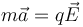
$m\vec{a}=q\vec{E}$

y en esta ecuación es claro que la masa, que mide la inercia, y la carga, que mide la respuesta a los campos eléctricos, son propiedades diferentes. Volviendo al caso del peso

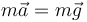
$m\vec{a}=m\vec{g}$

la masa del primer miembro mide la inercia como antes, mientras que la segunda mide la respuesta al campo gravitatorio. No tendrían por qué ser iguales, pero lo son. Newton fue el primero en establecer este principio de equivalencia entre la masa inercial y la gravitatoria y en hacer medidas experimentales para comprobarlo. Las últimas medidas experimentales confirman la igualdad de ambas masas hasta una precisión de una parte entre cada 100 billones.

El principio de equivalencia provoca que en determinadas situaciones la aceleración sea indistinguible de la gravedad. El ejemplo típico es el del ascensor cerrado.

Si nos imaginamos una nave espacial sin ventanas y una persona de pie en su interior, esta persona no sabría si se encuentra parado en la superficie de un planeta, y nota su peso, o si está viajando por el espacio con aceleración constante.

Igualmente, si una persona está dentro de un ascensor en el momento en que se corta el cable que lo sujeta, durante la caída de ambos, asecensor y pasajero, éste se encuentra en una situación de ingravidez aparente.

Este es el mismo principio por el que vemos flotar a los astronautas de la estación espacial. No porque a ella no llegue el campo gravitatorio terrestre (está solo a 500km de altura), sino porque la nave y sus ocupantes están cayendo.

2.2 En presencia de rozamiento

En una caída en la atmósfera terrestre, al peso debemos añadir el efecto de la fricción con el aire

$m\vec{a}=m\vec{g}+\vec{F}_r$

La fuerza de rozamiento en un fluido (rozamiento viscoso) depende de diferentes factores:

Densidad y viscosidad del fluido
Velocidad con la que se mueve el fluido
Tamaño y forma del objeto que cae
Velocidad con la que cae

Por ello, la expresión de una ley para el rozamiento viscoso es un problema complejo y normalmente se hacen aproximaciones. En la sección sobre rozamiento indicamos los dos casos más usuales.

Una consecuencia importante de la presencia de rozamiento viscoso es la existencia de una velocidad límite. Mientras que en ausencia de rozamiento el movimiento de una partícula es acelerado y la rapidez crece sin límite hasta el momento del impacto, cuando existe rozamiento viscoso la velocidad tiende hacia un valor límite en el que se cancelan mutuamente el peso y la fuerza de rozamiento.

3 Movimiento orbital. Ley de la Gravitación Universal

Se dice que un cuerpo está en caída libre cuando se mueve sometido exclusivamente a la acción de la gravedad. Puesto que la Luna se mueve exclusivamente por acción de la gravedad, está cayendo. Y si la Luna está cayendo, ¿por qué no impacta con la Tierra?

La razón es que la Luna “esquiva” a la Tierra por su movimiento lateral. Si nos imaginamos que estamos en lo alto de una alta montaña y disparamos un proyectil horziontalmente con una cierta velocidad pequeña, describirá una parábola y acabará impactando con el suelo. Si la velocidad de lanzamiento es mayor, conseguirá volar más tiempo y el punto de impacto estará más alejado. Si se le da la velocidad suficiente, describirá una órbita circular y habrá conseguido entrar en órbita.

¿Qué velocidad necesita para entrar en órbita? Supongamos que inicialmente se encuentra a una distancia $y 0 = r$ del centro de la Tierra y consideramos su movimiento en un tiempo pequeño $Δ t$ . En ese tiempo habrá descendido a una altura

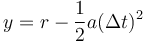
$y = r - \frac{1}{2}a(\Delta t)^2$

pero simultáneamente se habrá movido lateralmente una cantidad

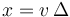
$x = v \,\Delta$

La clave de que describa una órbita circular es que tras este movimiento siga a la misma distancia del centro

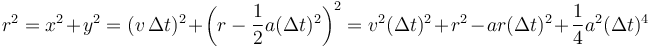
$r^2 = x^2 + y^2 = (v\,\Delta t)^2 + \left(r-\frac{1}{2}a(\Delta t)^2\right)^2 = v^2(\Delta t)^2 + r^2 - a r(\Delta t)^2+\frac{1}{4}a^2(\Delta t)^4$

Eliminando $r 2$ y simplificando queda

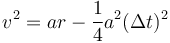
$v^2 = ar -\frac{1}{4}a^2(\Delta t)^2$

El último término es despreciable por ser muy pequeño el intervalo de tiempo. Por ello queda que la rapidez necesaria es

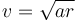
$v = \sqrt{a r}$

o, lo que es lo mismo

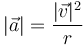
$|\vec{a}| = \frac{|\vec{v}|^2}{r}$

Esta no es otra que la fórmula para la aceleración normal. Este resultado era de esperar, ya que estamos considerando que la Luna describe un movimiento circular uniforme.

A partir de este resultado y del hecho conocido de la caída de la manzana, Newton pudo establecer su ley de la Gravitación Universal. Se preguntó, ¿qué tipo de fuerza sería responsable del movimiento tanto de una manzana como de la Luna? La aceleración de la manzana por acción de la gravedad es bien conocida

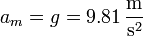
$a_m = g = 9.81\,\frac{\mathrm{m}}{\mathrm{s}^2}$

¿Cuánto vale la aceleración de la Luna? Ésta describe un movimiento circular en torno a la Tierra, con aceleración

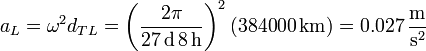
$a_L = \omega^2 d_{TL} = \left(\frac{2\pi}{27\,\mathrm{d}\,8\,\mathrm{h}}\right)^2(384000\,\mathrm{km})= 0.027\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Comparando estas aceleraciones

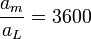
$\frac{a_m}{a_L}=3600$

Por otro lado, Newton sabía que

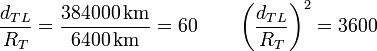
$\frac{d_{TL}}{R_T}=\frac{384000\,\mathrm{km}}{6400\,\mathrm{km}}=60\qquad \left(\frac{d_{TL}}{R_T}\right)^2=3600$

por lo que se cumple, aproximadamente, que

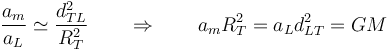
$\frac{a_m}{a_L}\simeq \frac{d_{TL}^2}{R_T^2}\qquad\Rightarrow\qquad a_m R_T^2 = a_L d_{LT}^2 = GM$

(siendo GM una constante independiente de la manzana y de la Luna) y por tanto

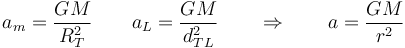
$a_m = \frac{GM}{R_T^2}\qquad a_L=\frac{GM}{d_{TL}^2}\qquad\Rightarrow\qquad a = \frac{GM}{r^2}$

esto es que simplemente imponiendo que la misma fuerza que hace caer a la manzana es la que mueve a la Luna, consiguió establecer que la ley de la gravitación va como la inversa del cuadrado.

4 La tercera ley de Kepler

A partir de la ley de la Gravitación Universal Newton probó que puede demostrarse la tercera ley de Kepler.

Si los planetas describen órbitas circulares con rapidez constante, su única aceleración es la normal. Por tanto

$\frac{|\vec{v}|^2}{R}=\frac{|\vec{F}|}{m}=\frac{GM}{R^2}$

siendo la rapidez igual a la distancia recorrida (la longitud de la órbita) dividida por el tiempo en hacerlo (el periodo orbital)

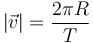
$|\vec{v}|=\frac{2\pi R}{T}$

por lo que

$\frac{4\pi^2 R}{T^2}= \frac{GM}{R^2}\qquad\Rightarrow\qquad T^2 = \frac{4\pi^2}{GM}R^3$

que es la tercera ley de Kepler: los cuadrados de los periodos son proporcionales a los cubos de los radios de las órbitas.

Esta “demostración” no es muy rigurosa en cuanto a que las órbitas planetarias son elipses. No obstante, puede demostrarse (aunque es más complicado) también para ese caso, cambiando los radios por los semiejes mayores.

Experimentalmente, la prueba es contundente: tabulando los valores de los periodos y los radios y representándolos en una gráfica logarítmica

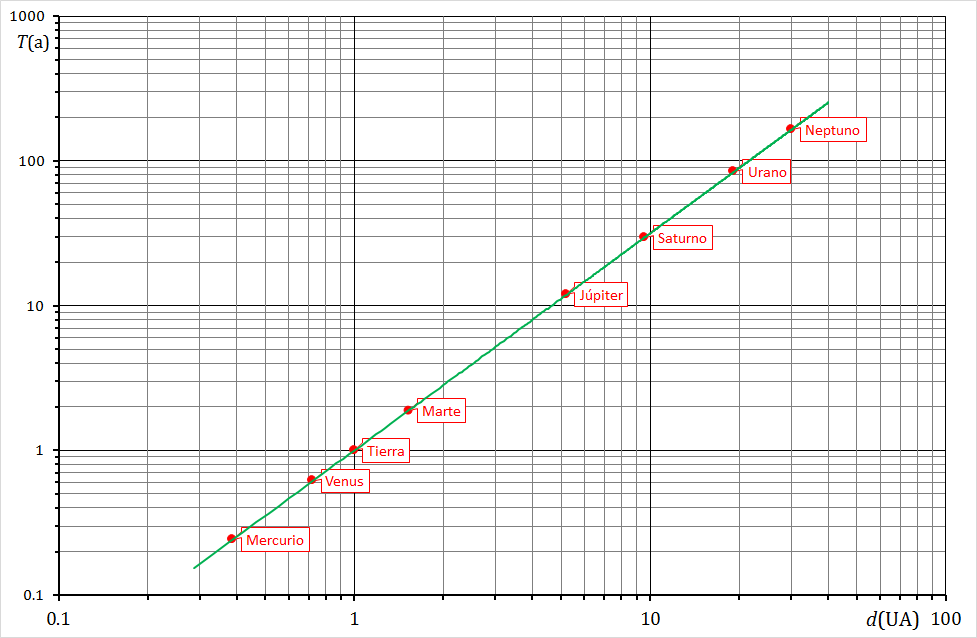
En esta gráfica, el eje de abcisas se mide en unidades astronómicas (UA, siendo 1UA el radio medio de la órbita terrestre, unos 150 millones de km) y el de ordenadas en años.

En una gráfica logarítmica, una ley potencial se convierte en una recta, siendo la pendiente igual al exponente. En este caso la teoría da que debe ser 1.5 y la experiencia que es 1.4994(11).

5 Gravedad y geometría

La teoría de newton de la Gravitación Universal explica la mayoría de los fenómenos asociados a la gravedad pero no todos.

Tras elaborar su teoría de la relatividad especial, Einstein desarrolló una teoría de la gravitación que era compatible con la teoría de la relatividad especial. El resultado fue la teoría de la relatividad general (TRG). En la TRG la gravedad se convierte en una curvatura del espacio tiempo y las órbitas de los planetas y otros cuerpos no son debidas a que actúa una fuerza sobre ellos, sino a que el espacio-tiempo por el que se mueven está curvado.

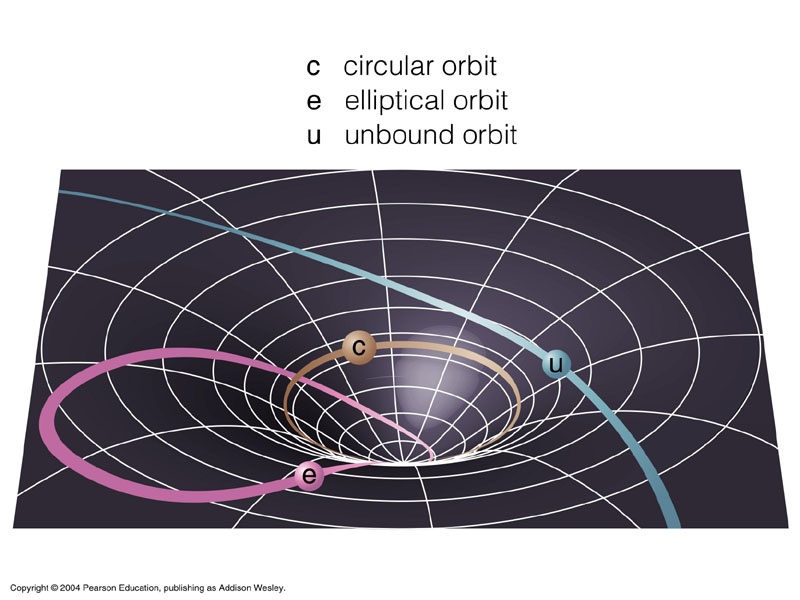
Una de las predicciones más llamativas de la TRG es la existencia de agujeros negros, de los cuales ni la luz puede escapar. Actualmente hay fuertes indicios de la existencia real de estos agujeros negros.

No se ha encontrado, en cambio, ningún agujero de gusano, también posibles de acuerdo con esta teoría.

Movimiento de una partícula por acción de la gravedad (GIOI)

De Laplace

Contenido

1 Gravedad y peso

2 Movimiento en las proximidades de la Tierra

2.1 Sin rozamiento con el aire

2.2 En presencia de rozamiento

3 Movimiento orbital. Ley de la Gravitación Universal

4 La tercera ley de Kepler

5 Gravedad y geometría

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES