Momento cinético (CMR)

De Laplace

Contenido

1 Definiciones
- 1.1 Momento cinético
- 1.2 Momento de una fuerza
2 Propiedades del momento cinético
3 Interpretación del momento cinético
4 Cambio del centro de reducción
5 Derivada del momento cinético (Teorema del momento cinético)
6 Teorema de conservación
7 Fuerzas centrales
8 Segunda ley de Kepler
9 Expresión en coordenadas polares
10 Conservación parcial del momento cinético
11 Ejemplo. Péndulo simple
12 Para un sistema de partículas
13 Teorema de König. Descomposición del momento angular
14 Evolución del momento cinético de un sistema
- 14.1 Para un punto fijo O
- 14.2 Para un punto móvil
  - 14.2.1 Momento cinético absoluto
  - 14.2.2 Momento cinético relativo
15 Teorema de conservación del momento cinético
16 El caso del peso

1 Definiciones

1.1 Momento cinético

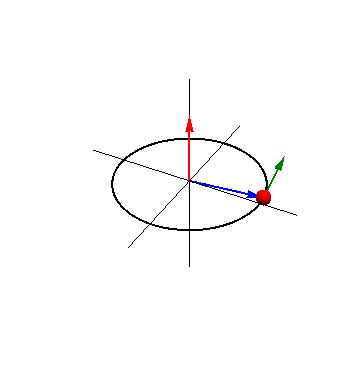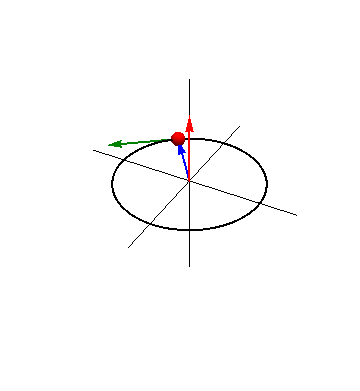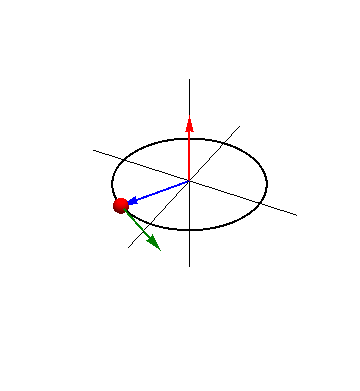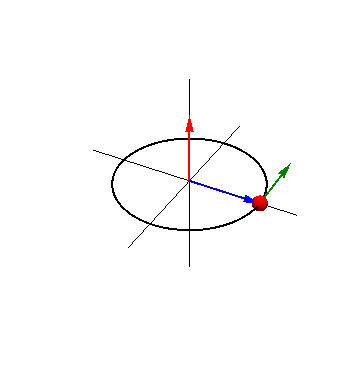
Se define el momento cinético (o momento angular) de una partícula respecto a un punto fijo O como

$\vec{L}_O = \vec{r}\times\vec{p}=m\vec{r}\times\vec{v}$

siendo

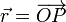
$\vec{r}=\overrightarrow{OP}$

el vector de posición del punto P relativa al punto O.

La condición de que el punto O sea fijo es importante, ya que la velocidad se mide respecto a ese punto. Cuando el punto es móvil, como veremos más adelante, hay que aclarar si hablamos de la velocidad absoluta o de la relativa respecto a O.

1.2 Momento de una fuerza

Se define el momento respecto a un punto fijo O de una fuerza aplicada en un punto P como el producto vectorial

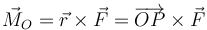
$\vec{M}_O = \vec{r}\times\vec{F}=\overrightarrow{OP}\times\vec{F}$

Al momento de una fuerza también se lo denomina “el par de la fuerza” o (por contagio del inglés) el “torque”.

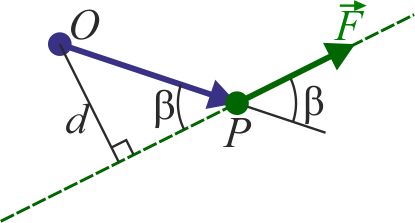
El módulo del momento de una fuerza es igual a

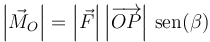
$\left|\vec{M}_O\right| = \left|\vec{F}\right|\left|\overrightarrow{OP}\right|\,\mathrm{sen}(\beta)$

pero

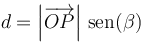
$d = \left|\overrightarrow{OP}\right|\,\mathrm{sen}(\beta)$

es la distancia a la llamada recta soporte, que es aquella que pasa por P y tiene la dirección de la fuerza. Por tanto, el módulo del momento de la fuerza se puede escribir

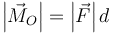
$\left|\vec{M}_O\right| = \left|\vec{F}\right|d$

A la distancia $d$ se la denomina “brazo del momento” o “brazo del par”. De aquí resulta que el valor del momento de una fuerza no depende de la posición exacta del punto P, sino solo de la recta soporte donde se halla.

La dirección del momento de la fuerza es perpendicular al plano definido por $\overrightarrow{OP}$ y la fuerza (es decir, el que contiene a O y a la recta soporte). Su sentido lo da la regla de la mano derecha. Si O está a un lado de la recta soporte, el sentido del momento es hacia afuera del plano; si está al otro es hacia adentro. Cuando el propio punto O se encuentra en la recta soporte

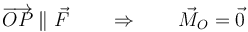
$\overrightarrow{OP}\parallel \vec{F} \qquad\Rightarrow\qquad \vec{M}_O=\vec{0}$

Si tenemos varias fuerzas actuando sobre la misma partícula, la resultante de los momentos es igual al momento de la resultante

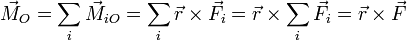
$\vec{M}_O=\sum_i \vec{M}_{iO}=\sum_i\vec{r}\times\vec{F}_i = \vec{r}\times\sum_i\vec{F}_i =\vec{r}\times\vec{F}$

2 Propiedades del momento cinético

2.1 Módulo, dirección y sentido

El momento cinético de una partícula es un vector ortogonal al vector de posición relativo y a la velocidad. Por tanto, es normal al plano definido por ambos. Su sentido lo da la regla de la mano derecha. El módulo es igual a

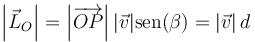
$\left|\vec{L}_O\right| = \left|\overrightarrow{OP}\right||\vec{v}|\mathrm{sen}(\beta)=\left|\vec{v}\right| d$

siendo $d$ en este caso la distancia de $O$ a la recta tangente al movimiento.

2.2 Caso del movimiento plano

Si una partícula describe un movimiento plano, podemos elegir los ejes de coordenadas para que este plano sea el XY. En este caso, el momento cinético respecto a un punto O, situado en el plano de movimiento, tiene una expresión sencilla: el momento cinético es perpendicular al plano de movimiento y por tanto tiene una sola componente, pudiéndose tratar como un escalar

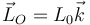
$\vec{L}_O=L_0\vec{k}$

En cartesianas: De la definición

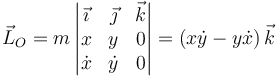
$\vec{L}_O=m\left|\begin{matrix}\vec{\imath}& \vec{\jmath} & \vec{k} \\ x & y & 0 \\ \dot{x} & \dot{y} & 0\end{matrix}\right|=\left(x\dot{y}-y\dot{x}\right)\vec{k}$

En coordenadas polares: Aún más simple es la expresión en polares para el caso del movimiento plano

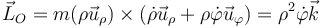
$\vec{L}_O=m(\rho\vec{u}_\rho)\times(\dot{\rho}\vec{u}_\rho+\rho\dot{\varphi}\vec{u}_\varphi)=\rho^2\dot{\varphi}\vec{k}$

2.3 Caso tridimensional

Operando de la misma manera hallamos las componentes en cartesianas en un movimiento general

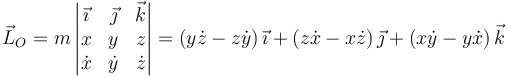
$\vec{L}_O=m\left|\begin{matrix}\vec{\imath}& \vec{\jmath} & \vec{k} \\ x & y & z \\ \dot{x} & \dot{y} & \dot{z}\end{matrix}\right|=\left(y\dot{z}-z\dot{y}\right)\vec{\imath}+\left(z\dot{x}-x\dot{z}\right)\vec{\jmath}+\left(x\dot{y}-y\dot{x}\right)\vec{k}$

3 Interpretación del momento cinético

Del mismo modo que la cantidad de movimiento, como su nombre indica, es una medida de cuánto se mueve una partícula (en el sentido de que, por ejemplo, en una colisión, importa tanto la velocidad del proyectil como su masa), el momento cinético mide la cantidad de rotación en torno al punto O.

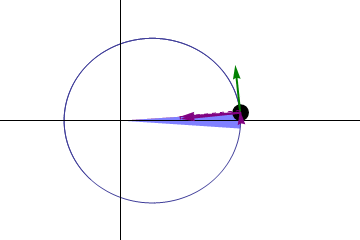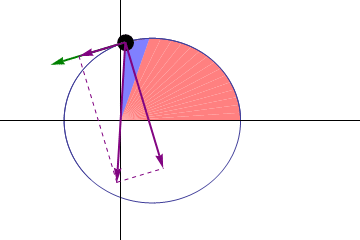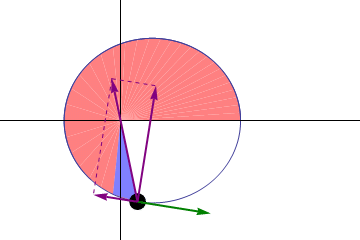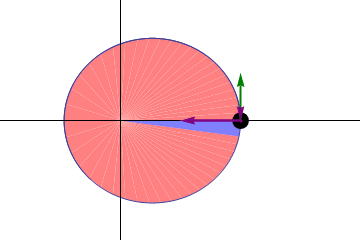
Esto se ve claro en el caso de un movimiento circular. Si una partícula describe una circunferencia alrededor del punto O, el momento cinético respecto a este punto vale

$\vec{L}_O = m\vec{r}\times\vec{v}=m\vec{r}\times(\vec{\omega}\times\vec{r}) = mR^2\vec{\omega}$

Vemos que esta “cantidad de rotación” depende de con qué velocidad se gira, de la masa de la partícula y del radio de la circunferencia.

Esta idea se puede generalizar a movimientos no circulares. Si una partícula describe un movimiento rectilíneo y la observamos desde un punto exterior a la recta, nuestra dirección de observación va girando, aunque la partícula vaya en línea recta. Eso sí, cuanto mayor es la distancia, menor es el cambio de la dirección de observación.

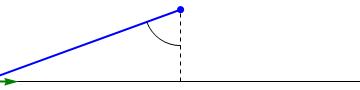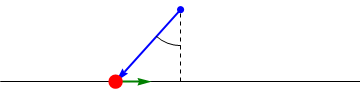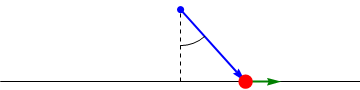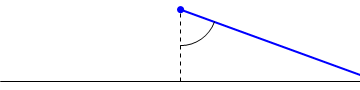
4 Cambio del centro de reducción

Si en vez de un punto O, calculamos el momento cinético respecto a otro punto fijo A (lo que dice, en un contexto más gfeneral “cambiar el centro de reducción”)

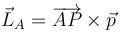
$\vec{L}_A = \overrightarrow{AP}\times\vec{p}$

la relación con el del punto O es

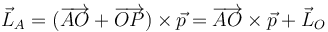
$\vec{L}_A=(\overrightarrow{AO}+\overrightarrow{OP})\times\vec{p}=\overrightarrow{AO}\times\vec{p}+\vec{L}_O$

siendo el vector $\overrightarrow{AO}$ uno fijo, independiente del movimiento de la partícula. Invirtiendo el producto vectorial

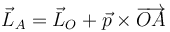
$\vec{L}_A=\vec{L}_O+\vec{p}\times\overrightarrow{OA}$

Igualmente, para el momento de las fuerzas, tenemos que

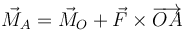
$\vec{M}_A = \vec{M}_O+\vec{F}\times\overrightarrow{OA}$

siendo $\vec{F}$ la resultante de las fuerzas aplicadas

5 Derivada del momento cinético (Teorema del momento cinético)

Como consecuencia de la segunda ley de Newton, la derivada del momento cinético de una partícula es igual al momento resultante sobre ella

$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} =m\left(\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right)\times\vec{v}+m\,\vec{r}\times\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\overbrace{\vec{v}\times\vec{v}}^{=\vec{0}}+\vec{r}\times\vec{F}=\vec{M}_O$

Nótese que para que esta expresión sea correcta, es crucial que el punto O sea fijo. Si no, deberíamos tener en cuenta su velocidad a la hora de derivar.

6 Teorema de conservación

De la expresión para la derivada del momento cinético se deduce su teorema de conservación:

Si la resultante de los momentos de las fuerzas que actúan sobre una partícula es nula, el momento cinético de dicha partícula permanece constante.

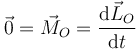
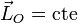
$\vec{0} = \vec{M}_O=\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}$ $\Rightarrow$ $\vec{L}_O=\mathrm{cte}$

Una consecuencia inmediata de la conservación del momento cinético es:

La trayectoria de una partícula cuyo momento cinético permanece constante es plana.

El plano en el que ocurre la trayectoria es el definido por el centro de reducción, la posición inicial y la velocidad inicial.

Puesto que el momento cinético se conserva tenemos que si multiplicamos escalarmente el vector de posición relativo por este vector constante

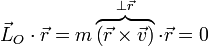
$\vec{L}_O\cdot\vec{r}=m\overbrace{\left(\vec{r}\times\vec{v}\right)}^{\perp\vec{r}}\cdot\vec{r} = 0$

Esta es la ecuación vectorial de un plano que pasa por O y es normal a la dirección de $\vec{L}_O$ .

7 Fuerzas centrales

Las fuerzas centrales constituyen un caso particular e importante de las diferentes fuerzas presentes en la naturaleza. Una fuerza central es aquella que en todos los puntos del espacio posee dirección radial desde un punto fijo O, siendo además dependiente solo de la distancia a dicho punto

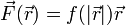
$\vec{F}(\vec{r}) = f(|\vec{r}|)\vec{r}$

Ejemplos de fuerzas centrales son la fuerza de la gravedad debida a un objeto masivo (como la atracción que el Sol ejerce sobre la Tierra), o la fuerza eléctrica debida a una carga en reposo.

Se tiene que

El momento cinético respecto a un punto O de una partícula sometida a la acción de una fuerza central, con centro O, permanece constante.

La demostración es inmediata, ya que el vector de posición relativo y la fuerza son vectores paralelos

$\vec{M}_O = \vec{r}\times\overbrace{\vec{F}}^{\parallel\vec{r}} = \vec{0}\qquad\Rightarrow\qquad \vec{L}_O = \mathrm{cte}$

En particular, esto implica que la trayectoria de toda partícula sometida a una fuerza central (p.ej. una óirbita planetaria, o un oscilador armónico en 3 dimensiones) es una curva plana.

Un detalle importante a tener en cuenta es que tener dos centros es lo mismo que no tener ninguno. La fuerza gravitatoria o la eléctrica son fuerzas centrales, pero solo cuando se consideran actuando en exclusividad y respecto a un punto fijo. Si hay más de un centro de atracción (por ejemplo, un satélite que se mueve en el campo gravitatorio combinado de la Tierra y la Luna) ya la fuerza resultante no es central y el momento cinético del satélite no se conservará en general.

8 Segunda ley de Kepler

La segunda ley de Kepler fue formulada inicialmente para el movimiento planetario, pero se trata de una consecuencia general de la ley de conservación del momento cinético.

Una partícula cuyo momento cinético permanece constante barre áreas iguales en tiempos iguales

Aquí la velocidad con la que se “barren áreas” hay que entenderla empleando la velocidad areolar: para una trayectoria plana se mide el ritmo con el que varía el área del triángulo mixtilíneo formado por el vector de posición inicial (medido desde el punto $O$ respecto al cual se conserva el momento cinético), el vector de posición instantáneo, respecto al mismo origen, y el arco de trayectoria comprendido entre los dos puntos.

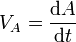
$V_A = \frac{\mathrm{d}A}{\mathrm{d}t}$

Puesto que posee dimensiones de L²/T, no se trata realmente de una velocidad, sino de un ritmo de variación.

En forma vectorial, si $\vec{B}$ es el vector perpendicular al plano que contiene a la trayectoria

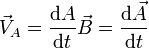
$\vec{V}_A = \frac{\mathrm{d}A}{\mathrm{d}t}\vec{B} = \frac{\mathrm{d}\vec{A}}{\mathrm{d}t}$

donde

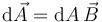
$\mathrm{d}\vec{A}=\mathrm{d}A\,\vec{B}$

es el vector diferencial de superficie, que tiene por módulo el área del elemento y por dirección la normal plano de la superficie.

En un intervalo infinitesimal $d t$ el área barrida es la correspondiente a un triángulo que tiene por lados el vector de posición relativo, $\vec{r}$ , y el desplazamiento diferencial

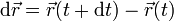
$\mathrm{d}\vec{r} = \vec{r}(t+\mathrm{d}t)-\vec{r}(t)$

el diferencial de superficie para este triángulo es

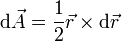
$\mathrm{d}\vec{A}=\frac{1}{2}\vec{r}\times\mathrm{d}\vec{r}$

y la velocidad areolar es igual a

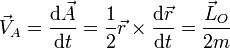
$\vec{V}_A = \frac{\mathrm{d}\vec{A}}{\mathrm{d}t}=\frac{1}{2}\vec{r}\times\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\frac{\vec{L}_O}{2m}$

Por tanto, si el momento cinético permanece constante, la velocidad areolar también es una integral primera y tenemos la segunda ley de Kepler.

La consecuencia inmediata de este teorema es que un cuerpo sometido a una fuerza central, por ejemplo, un planeta, se mueve más rápidamente cuando se encuentra en las proximidades del centro de fuerzas que cuando se encuentra más alejado de él.

Para el caso de la órbita terrestre, podemos comprobar que en invierno, la distancia Tierra-Sol es menor que en verano, pues mientras entre el equinoccio de Otoño (23 de septiembre) y el de Primavera (21 de marzo) hay 179 días, entre el de Primavera y el de Otoño hay 184 días, esto es, el invierno es más corto que el verano, debido a la mayor proximidad. Concretamente, el perihelio (punto más próximo) es en torno al 4 de enero, mientras que el afelio (punto más alejado) es en torno al 4 de Julio.

Este resultado también es aplicable al caso de una trayectoria abierta, incluyendo ahí el caso particular de un movimiento rectilíneo uniforme.

9 Expresión en coordenadas polares

El teorema del momento cinético presenta una expresión extremadamente sencilla en el caso de una partícula que efectúa un movimiento plano, si se emplean coordenadas polares.

Para un movimiento plano, el vector de posición de una partícula es

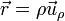
$\vec{r}=\rho\vec{u}_\rho$

y su velocidad

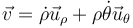
$\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\theta}\vec{u}_\theta$

Multiplicando vectorialmente estas dos cantidades obtenemos la velocidad areolar y el momento cinético respecto al origen de coordenadas

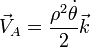
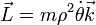
$\vec{V}_A=\frac{\rho^2\dot{\theta}}{2}\vec{k}$ $\vec{L}=m\rho^2\dot{\theta}\vec{k}$

La derivada temporal de esta expresión nos da

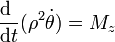
$\frac{\mathrm{d}\ }{\mathrm{d}t}(\rho^2\dot{\theta})=M_z$

En el caso de una fuerza central, esta se expresa en polares

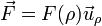
$\vec{F}=F(\rho)\vec{u}_\rho$

y la ecuación de movimiento correspondiente

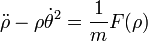
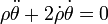
$\ddot{\rho}-\rho\dot{\theta}^2=\frac{1}{m}F(\rho)$ $\rho\ddot{\theta}+2\dot{\rho}\dot{\theta}=0$

La segunda ecuación es equivalente a la ley de conservación del momento cinético

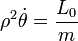
$\rho^2\dot{\theta}=\frac{L_0}{m}$

Despejando de aquí y sustituyendo en la componente radial de la aceleración queda

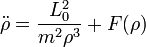
$\ddot{\rho}=\frac{L_0^2}{m^2\rho^3}+F(\rho)$

que matemáticamente es equivalente a una ecuación de movimiento rectilíneo, con un término de fuerza adicional.

10 Conservación parcial del momento cinético

Existen ocasiones en que el momento cinético no se conserva. Sin embargo, incluso en esos casos es a menudo posible obtener una ley de conservación más restringida.

Para ello, tenemos en cuenta que el momento cinético es un vector y posee tres componentes. Puede ocurrir que aunque el vector como tal no sea constante, una de sus componentes sí lo sea. Sea $\vec{u}$ un vector unitario fijo. La componente del momento angular según la dirección de $\vec{u}$ es

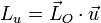
$L_{u}=\vec{L}_O\cdot\vec{u}\,$

Derivando aquí respecto al tiempo

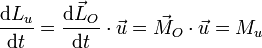
$\frac{\mathrm{d}L_u}{\mathrm{d}t}=\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\cdot\vec{u}=\vec{M}_O\cdot\vec{u}=M_u$

Si se anula la componente en la dirección de $\vec{u}$ del momento de las fuerzas aplicadas, la componente del momento cinético en dicha dirección permanece constante.

11 Ejemplo. Péndulo simple

Un ejemplo de aplicación del teorema del momento cinético en el que se simplifican los cálculos respecto a la aplicación directa de las leyes de Newton es el caso del péndulo simple.

Supongamos una partícula de masa $m$ atada a un hilo inextensible que por su otro extremo está atado a un punto de anclaje fijo O.

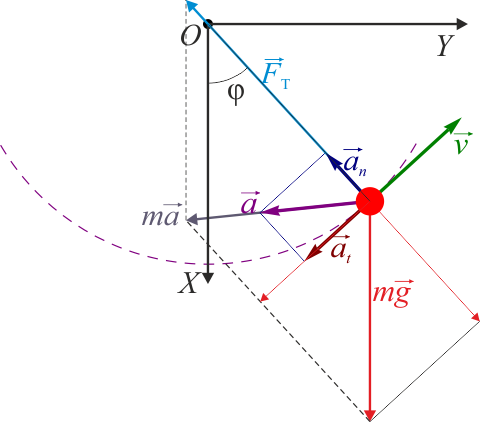
Tal como se ve en el apartado correspondiente de aplicaciones de las leyes de Newton, la masa se encuentra sometida a la acción conjunto de dos fuerzas: el peso y la tensión del hilo, de forma que

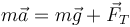
$m\vec{a}=m\vec{g}+\vec{F}_T$

Desarrollando esta ecuación en sus componentes y eliminando la tensión entre las dos ecuaciones que resultan se llega a la ecuación del péndulo

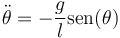
$\ddot{\theta}=-\frac{g}{l}\mathrm{sen}(\theta)$

la complicación que tiene este método es que obliga a introducir la tensión, que es una fuerza desconocida a priori.

Veamos como sería con ayuda del momento cinético. El momento cinético respecto al punto O es igual a

$\vec{L}_O=m\vec{r}\times\vec{v}$

donde

$\vec{r}=l\vec{u}_\rho\qquad \vec{v}=l\dot{\varphi}\vec{u}_\varphi$

Al ser perpendiculares estos dos vectores, su producto vectorial es igual a

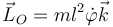
$\vec{L}_O=ml^2\dot{\varphi}\vec{k}$

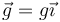siendo $\vec{k}$ el vector normal hacia afuera del plano de oscilación del péndulo (no el de la dirección de la gravedad, que en estos ejes sería $\vec{g}=g\vec{\imath}$ ). La derivada respecto al tiempo del momento cinético es

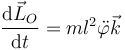
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=ml^2\ddot{\varphi}\vec{k}$

Esta derivada debe ser igual a la resultante de los momento de las fuerzas aplicadas

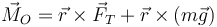
$\vec{M}_O=\vec{r}\times\vec{F}_T+\vec{r}\times(m\vec{g})$

Ahora bien, la tensión va en la dirección del hilo, que es también la del vector de posición. Por tanto, su momento es nulo y solo queda el del peso. Éste, a su vez, es igual a la distancia a la recta soporte (la vertical que pasa por la partícula), con lo que su momento vale

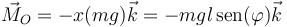
$\vec{M}_O=-x(mg)\vec{k} = -mgl\,\mathrm{sen}(\varphi)\vec{k}$

el signo negativo viene de que cuando $\varphi$ es positivo, la regla de la mano derecha da para el momento un sentido hacia adentro del plano.

Igualando las dos cantidades queda

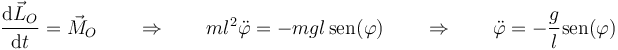
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O\qquad\Rightarrow\qquad ml^2\ddot{\varphi}=-mgl\,\mathrm{sen}(\varphi)\qquad\Rightarrow\qquad \ddot{\varphi}=-\frac{g}{l}\mathrm{sen}(\varphi)$

12 Para un sistema de partículas

12.1 Momento cinético respecto a un punto fijo

De manera análoga a la cantidad de movimiento, se define el momento cinético (o angular) de un sistema de partículas respecto a un punto fijo O (centro de reducción) como la suma vectorial de los momentos cinéticos individuales respecto a dicho punto

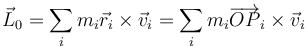
$\vec{L}_0=\sum_i m_i\vec{r}_i\times\vec{v}_i=\sum_im_i\overrightarrow{OP}_i\times\vec{v}_i$

12.2 Cambio del centro de reducción

Si en lugar de un punto fijo O calculamos el momento cinético respecto a otro punto A, la relación entre ambas cantidades es la misma que para una sola partícula

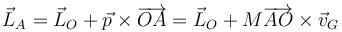
$\vec{L}_A=\vec{L}_O+\vec{p}\times\overrightarrow{OA}=\vec{L}_O+M\overrightarrow{AO}\times\vec{v}_G$

donde ahora 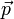$\vec{p}$ es la cantidad de movimiento del sistema completo.

En el caso particular de que O sea la posición instantánea del CM esta ecuación queda

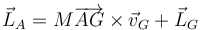
$\vec{L}_A=M\overrightarrow{AG}\times\vec{v}_G+\vec{L}_G$

12.3 Momento cinético respecto a un punto móvil

El punto O de referencia puede tener movimiento propio (un ejemplo típico es el centro de masas). En ese caso, tenemos dos posibles definiciones de momento cinético:

Una en la que el punto O se trata como un punto fijo (diferente en cada instante), en cuyo caso se aplica la fórmula anterior.
Una en la que se considera el movimiento de las partículas respecto al punto O, empleando las velocidades relativas a un sistema de referencia que se traslada con el punto.

El momento cinético relativo a este punto móvil será igual a

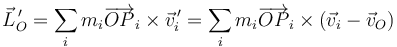
$\vec{L}^{\,\prime}_O=\sum_im_i \overrightarrow{OP}_i\times \vec{v}^{\,\prime}_i=\sum_im_i \overrightarrow{OP}_i\times (\vec{v}_i-\vec{v}_O)$

El momento cinético relativo se relaciona con el absoluto como

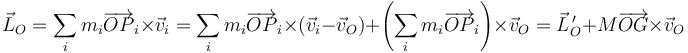
$\vec{L}_O=\sum_im_i \overrightarrow{OP}_i\times \vec{v}_i=\sum_im_i \overrightarrow{OP}_i\times (\vec{v}_i-\vec{v}_O)+\left(\sum_im_i\overrightarrow{OP}_i\right)\times\vec{v}_O =\vec{L}^{\,\prime}_O+M\overrightarrow{OG}\times\vec{v}_O$

Como caso particular importante de punto móvil tenemos el centro de masas. Para este punto se cumple que

$\vec{L}_G=\vec{L}^{\,\prime}_G\qquad\qquad (\overrightarrow{GG}=\vec{0})$

es decir, para el centro de masas es indiferente que lo tratemos como punto fijo o como punto móvil.

13 Teorema de König. Descomposición del momento angular

Las ecuaciones de la dinámica de sistemas se simplificarían notablemente si el momento angular, como la cantidad de movimiento, equivaliera al de una partícula puntual que concentrara toda la masa. No es así.

Antes hemos relacionado el momento cinético respecto a un punto fijo con el obtenido respecto al CM pero suponiendo que éste es también un punto fijo. Dado que en realidad se trata de un punto móvil, es adecuado tener en cuenta la velocidad relativa a este punto.

Según acabamos de ver, tanto si tratamos el CM como un punto fijo como si lo consideramos móvil se cumple

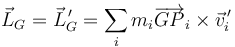
$\vec{L}_G=\vec{L}^{\,\prime}_G=\sum_i m_i\overrightarrow{GP}_i\times \vec{v}^{\,\prime}_i$

Aplicando la relación entre el momento calculado respecto a diferentes puntos obtenemos que, para un punto fijo O

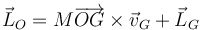
$\vec{L}_O= M\overrightarrow{OG}\times\vec{v}_G+\vec{L}_G$

y para uno considerado móvil

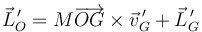
$\vec{L}^{\,\prime}_O= M\overrightarrow{OG}\times\vec{v}^{\,\prime}_G+\vec{L}^{\,\prime}_G$

Según esto, el momento angular o cinético de un sistema de partículas se compone de dos contribuciones: el momento angular que tendría una partícula que contuviera toda la masa y se moviera como el centro de masas del sistema, más el momento angular que tienen las partículas por moverse alrededor del centro de masas.

Un ejemplo físico sencillo de esta descomposición lo tenemos en el momento angular de la Tierra en cuanto planeta del Sistema Solar. Su momento angular se compone de una parte debida al movimiento de traslación alrededor del Sol (lo que se conoce como momento angular orbital), que sería el primer término, más otra parte debida al movimiento de rotación alrededor de su eje (el llamado momento angular intrínseco), que sería 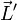$\vec{L}'$ .

Si el sistema está compuesto de varias partes, el momento cinético total será la suma de las distintas partes

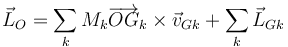
$\vec{L}_O=\sum_k M_k \overrightarrow{OG}_k\times\vec{v}_{Gk} +\sum_k \vec{L}_{Gk}$

Para el primer sumando podemos aplicar de nuevo el teorema de König, tratando cada parte como una partícula situada en su respectivo centro de masas. El segundo sumando representa los momentos cinéticos internos de cada parte. Así, en el ejemplo del Sistema Solar, el primer sumatorio correspondería a considerar éste como un sistema de 9 partículas puntuales y el segundo sumatorio incluiría los momentos cinéticos de rotación de los planetas y el Sol.

14 Evolución del momento cinético de un sistema

14.1 Para un punto fijo O

Derivando en la expresión del momento cinético de un sistema de partículas obtenemos

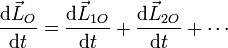
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} = \frac{\mathrm{d}\vec{L}_{1O}}{\mathrm{d}t} + \frac{\mathrm{d}\vec{L}_{2O}}{\mathrm{d}t} + \cdots$

Para cada partícula la derivada del momento angular es el momento resultante de las fuerzas aplicadas sobre ella:

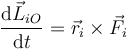
$\frac{\mathrm{d}\vec{L}_{iO}}{\mathrm{d}t}= \vec{r}_i\times\vec{F}_i$

y, para el momento cinético total

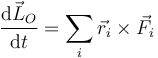
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}= \sum_i\vec{r}_i\times\vec{F}_i$

De nuevo, esta expresión requiere conocer las fuerzas internas del sistema, que son usualmente desconocidas. Por ello, descomponemos de nuevo en sumas de fuerzas externas e internas

$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}= \vec{r}_1\times\left(\vec{F}_{1\mathrm{ext}}+\vec{F}_{2\to 1}+\cdots\right) + \vec{r}_2\times\left(\vec{F}_{2\mathrm{ext}}+\vec{F}_{1\to 2}+\cdots\right)+ \cdots$

Las fuerzas newtonianas, que verifican la tercera ley de Newton, no solo cumplen que son iguales y opuestas, sino que además van en la dirección de la recta que une las dos partículas

$\vec{F}_{1\to 2}=-\vec{F}_{2\to 1}\qquad\qquad (\vec{r}_2-\vec{r}_1)\times\vec{F}_{1\to 2}=\vec{0}$

Combinando las dos ecuaciones queda

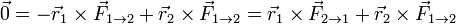
$\vec{0}= -\vec{r}_1\times\vec{F}_{1\to 2}+\vec{r}_2\times\vec{F}_{1\to 2}= \vec{r}_1\times\vec{F}_{2\to 1}+\vec{r}_2\times\vec{F}_{1\to 2}$

esto es, los momentos de las fuerzas internas se anulan mutuamente. Esta condición se cumple en la mayoría de los casos prácticos (fuerzas eléctricas o gravitatorias). En este caso, los momentos de las fuerzas internas se anulan dos a dos y queda

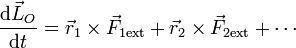
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}= \vec{r}_1\times\vec{F}_{1\mathrm{ext}}+\vec{r}_2\times\vec{F}_{2\mathrm{ext}}+\cdots$

En palabras:

La derivada del momento angular o cinético de un sistema de partículas es igual a la suma de los momentos de las fuerzas externas aplicadas sobre el sistema.

14.2 Para un punto móvil

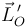Supongamos que el centro de reducción posee movimiento propio (es decir, en cada instante hallamos el momento respecto a un punto diferente). En ese caso, según hemos visto tenemos dos posibles definiciones de momento cinético, según si usamos las velocidad absolutas, $\vec{L}_O$ o las relativas $\vec{L}^{\,\prime}_O$ . Cada una de estas cantidades obedece una ley de evolución diferente, por lo que hay que ser cuidadoso con ellas.

14.2.1 Momento cinético absoluto

Cuando el propio punto O se mueve, la derivada de la posición relativa es la velocidad relativa

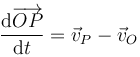
$\frac{\mathrm{d}\overrightarrow{OP}}{\mathrm{d}t}=\vec{v}_P-\vec{v}_O$

por ello, a la hora de derivar obtenemos

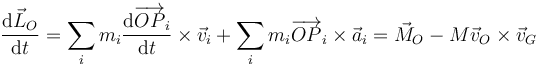
$\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\sum_i m_i \frac{\mathrm{d}\overrightarrow{OP}_i}{\mathrm{d}t}\times\vec{v}_i+\sum_i m_i\overrightarrow{OP}_i\times \vec{a}_i= \vec{M}_O-M\vec{v}_O\times\vec{v}_G$

En este caso, la derivada del momento cinético coincide con el momento resultante en los casos:

Que 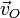$\vec{v}_O$ sea nulo, es decir que realmente se trate de un punto fijo (pero fijo, fijo; no vale que esté en un movimiento rectilíneo y uniforme).
Que 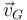$\vec{v}_G$ sea nulo, es decir, que el centro de masas esté inmóvil.
Que 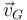$\vec{v}_G$ sea paralelo a 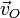$\vec{v}_O$ . Esto incluye el caso particular importante en que G = O, ya que entonces las dos velocidades son iguales, es decir,

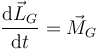
$\frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}= \vec{M}_G$

14.2.2 Momento cinético relativo

Si consideramos el momento calculado con las velocidades relativas

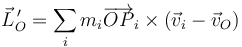
$\vec{L}^{\,\prime}_O=\sum_i m_i\overrightarrow{OP}_i\times(\vec{v}_i-\vec{v}_O)$

su derivada respecto al tiempo vale

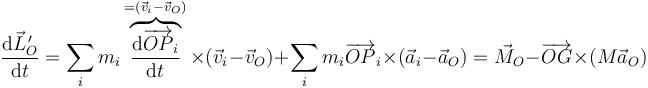
$\frac{\mathrm{d}\vec{L}^{\,\prime}_O}{\mathrm{d}t}=\sum_i m_i \overbrace{\frac{\mathrm{d}\overrightarrow{OP}_i}{\mathrm{d}t}}^{=(\vec{v}_i-\vec{v}_O)}\times(\vec{v}_i-\vec{v}_O)+\sum_i m_i\overrightarrow{OP}_i\times (\vec{a}_i-\vec{a}_O)= \vec{M}_O-\overrightarrow{OG}\times(M\vec{a}_O)$

Vemos que, como ocurre con la cantidad de movimiento, el resultado es equivalente a que a la hora de hallar los momentos de las fuerzas externas debemos incluir una fuerza ficticia de inercia aplicada en el centro de masas.

En este caso, la derivada del momento cinético coincide con el momento resultante en los casos:

Que 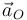$\vec{a}_O$ sea nulo, es decir que O esté en reposo o en movimiento rectilíneo y uniforme.
Que G = O, ya que entonces la posición relativa es nula, es deicr, también se cumple

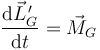
$\frac{\mathrm{d}\vec{L}^{\,\prime}_G}{\mathrm{d}t}= \vec{M}_G$

15 Teorema de conservación del momento cinético

Del teorema del momento cinético se deduce de manera inmediata que:

Si el momento resultante de las fuerzas externas aplicadas respecto a un punto fijo O es nulo durante un cierto intervalo de tiempo, el momento cinético respecto a dicho punto es constante.

En particular:

En un sistema de partículas sometido exclusivamente a fuerzas internas newtonianas, el momento cinético respecto a cualquier punto fijo es constante.

Los mismos resultados se tienen si en lugar de un punto fijo tomamos como centro de reducción el centro de masas G.

Para puntos móviles que no sean el CM habrá que analizar además si se cumplen las condiciones para que el segundo término de la igualdad se anule.

16 El caso del peso

Por su frecuencia en sistemas reales, es conveniente considerar el caso de que una de las fuerzas externas aplicadas al sistema se trate del peso de cada partícula. En ese caso tenemos

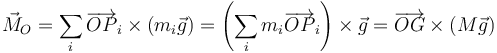
$\vec{M}_O=\sum_i \overrightarrow{OP}_i\times (m_i\vec{g})=\left(\sum_im_i\overrightarrow{OP}_i\right)\times\vec{g}=\overrightarrow{OG}\times(M\vec{g})$

Por tanto, desde el punto de vista del momento de las fuerzas, el sistema de pesos equivale al peso de una sola partícula situada en el centro de masas.

Esto implica que, en ausencia de otras fuerzas externas, el momento cinético respecto al CM de un sistema de partículas permanece constante. Para un centro de reducción fijo se conserva la componente del momento cinético en la dirección de la gravedad.