Medidas, estimaciones e incertidumbres

De Laplace

Contenido

1 Medidas, estimaciones e incertidumbres
2 Cifras significativas
3 Incertidumbres
4 Órdenes de magnitud
5 Estimaciones

1 Medidas, estimaciones e incertidumbres

Una medida es una comparación con una unidad, siendo esta arbitraria, como hemos dicho. Cada medida posee un valor numérico que expresa cuántas veces contiene a la unidad.. Así cuando decimos “tuve un accidente a mitad de camino”, matemáticamente se expresará

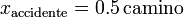
$x_\mathrm{accidente} = 0.5\,\mbox{camino}$

siendo “camino” nuestra unidad. Ahora bien, ese 0.5 sin duda no es una cantidad exacta, sino que se trata de una estimación bastante incierta. Incluso en las situaciones reales en las que se emplean aparatos de medida, los valores de éstas poseen una cierta incertidumbre, proveniente de las limitaciones del aparato de medida o de las condiciones en que se realiza esta. Lo mismo se aplica a toda cantidad derivada de una medida.

2 Cifras significativas

La primera expresión de que una cantidad es incierta la da el número de cifras significativas. Esta es la cantidad de cifras (que no de decimales) que conocemos con certeza y que informan del valor de la magnitud (y no de su tamaño, lo que sería su orden de magnitud, que veremos más adelante).

Por ejemplo, si medimos la longitud de una hoja tamaño A4 empleando una regla graduada en milímetros, obtenemos que su valor es

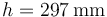
$h = 297\,\mathrm{mm}$

Esta cantidad tiene 3 cifras significativas, ya que sabemos que la primera es un 2, la segunda es un 9 y la tercera un 7. Podríamos expresar esta misma longitud en metros, centímetros o la que queramos

$h = 0.297\,\mathrm{m}=29.7\,\mathrm{cm}=0.000297\,\mathrm{km}=297000\,\mu\mathrm{m}$

y el número de cifras significativas sigue siendo tres, incluso en el último caso, en el que la medida se expresa como un número de seis cifras.

Hay veces en que el número de cifras significativas no está claro. Si nos dicen que el radio de la tierra es

$R_T = 6400\,\mathrm{km}$

¿tiene 2, 3 o 4 cifras significativas? Para estos casos ambiguos es preferible recurrir a la notación científica

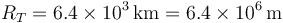
$R_T = 6.4\times 10^3\,\mathrm{km}=6.4\times 10^6\,\mathrm{m}$

que deja claro que tiene dos cifras significativas.

El valor de una medida podrá escribirse entonces en la notación científica, por ejemplo

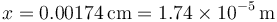
$x = 0.00174\,\mathrm{cm} = 1.74\times 10^{-5}\,\mathrm{m}$

donde la potencia de diez representa el orden de magnitud y lo que la multiplica (conocido como “la mantisa”) nos da la información de que disponemos sobre el valor de la medida.

Una regla básica de operación es que la incertidumbre de los datos se propaga a los resultados (“de donde no hay no se puede sacar”), de forma que si partimos de un dato con tres cifras significativas, no vamos a obtener un resultado con 10.

Por ejemplo, consideremos la fórmula de la velocidad de impacto de un proyectil en ausencia de rozamiento

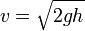
$v = \sqrt{2gh}$

y supongamos que queremos hallar la velocidad con la llega una partícula pesada que cae desde unos cinco metros de altura. Podríamos pensar que

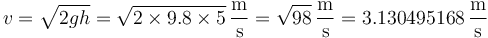$v = \sqrt{2 g h}= \sqrt{2\times 9.8\times 5}\,\frac{\mathrm{m}}{\mathrm{s}} = \sqrt{98} \,\frac{\mathrm{m}}{\mathrm{s}}= 3.130495168\,\frac{\mathrm{m}}{\mathrm{s}}$ (EXPRESIÓN INCORRECTA)

ya que esto implica que conoceríamos la velocidad con infinita precisión, lo cual es imposible. Teniendo en cuenta que hemos dado un periodo con una sola cifra significativa (“unos cinco metros”, puede ser también 5.1 metros o 4.9 metros), la expresión correcta del resultado sería

$v = \sqrt{2 g h}= \sqrt{2\times 9.8\times 5}\,\frac{\mathrm{m}}{\mathrm{s}} = \sqrt{98} \,\frac{\mathrm{m}}{\mathrm{s}}\simeq 3\,\frac{\mathrm{m}}{\mathrm{s}}$

3 Incertidumbres

Todo dato experimental, y toda cantidad obtenida a partir de medidas experimentales, además de poseer un cierto valor, lleva implícita una cierta incertidumbre (también conocida como “error”, aunque este término induce a confusión). Por las limitaciones de los aparatos de medida y por las condiciones en que se realizan éstas, todo lo más que se puede afirmar es que el resultado se encuentra dentro de un cierto rango.

Por ejemplo, si se mide el diámetro de una pelota de tenis con una regla graduada en milímetros y se obtiene un valor de 67 mm, lo más que se puede decir es que el diámetro se encuentra entre 66.5 mm y 67.5 mm (fuera de este rango ya la medida quedaría más cerca de las marcas vecinas en la regla). Diriamos entonces que la medida posee una incertidumbre de ±0.5 mm

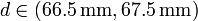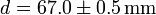
$d\in(66.5\,\mathrm{mm},67.5\,\mathrm{mm})$ o $d = 67.0\pm 0.5\,\mathrm{mm}$

A la hora de hablar de incertidumbre, hay que tener cuidado en distinguir que hay dos diferentes, relacionadas entre sí:

Incertidumbre absoluta, E: Es la mitad de la anchura de la banda de incertidumbre. Por convenio, se define esta anchura como la que da una probabilidad del 95% de que el valor de la medida quede dentro del intervalo

$\bar{x}-E_x < x < \bar{x}+E_x$

La incertidumbre absoluta tiene las mismas unidades que la magnitud a la cual limita.
Incertidumbre relativa, ε: es la proporción entre la incertidumbre absoluta y el valor establecido para la medida

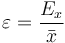
$\varepsilon = \frac{E_x}{\bar{x}}$

La incertidumbre relativa es una cantidad adimensional que suele medirse en tanto por ciento. También se la conoce como tolerancia.

Las incertidumbres se transmiten a los cálculos posteriores. Así, si queremos hallar el volumen de la pelota de tenis, suponiendo esta una esfera perfecta, tendríamos que

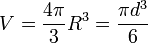
$V = \frac{4\pi}{3}R^3 = \frac{\pi d^3}{6}$

Considerando los valores extremos del diámetro quedaría el rango de volúmenes

$V\in \left(153980\,\mathrm{mm}^3,161031\,\mathrm{mm}^3\right)$

o, considerando el valor medio y la anchura del intervalo

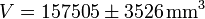
$V = 157505\pm 3526\,\mathrm{mm}^3$

Sin embargo, esta expresión tiene demasiadas cifras significativas. Si estamos diciendo que ya la tercera cifra del volumen es incierta, no sirve da nada dar el resto. Una expresión más corrrecta sería

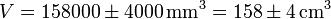
$V = 158000\pm 4000\,\mathrm{mm}^3=158\pm 4\,\mathrm{cm}^3$

Según esto, el conocimiento de la incertidumbre nos limita el número de cifras significativas.

La incertidumbre relativa del radio de la pelota sería

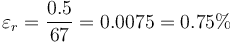
$\varepsilon_r=\frac{0.5}{67}=0.0075 = 0.75\%$

y la de su volumen

$\varepsilon_v=\frac{4}{158}=0.0253 = 2.53\%$

En la resolución de un problema de cuyos datos desconozcamos la incertidumbre, puede admitirse, como regla básica, que la incertidumbre la fija el dato más impreciso, siendo su número de cifras significativas el que deben tener aproximadamente los resultados.

4 Órdenes de magnitud

A la hora de resolver un problema, conviene siempre analizar los resultados con espíritu crítico y plantearse si son razonables o absurdos. Por ejemplo, en un examen reciente se preguntaba el tiempo necesario para derretir un bloque de medio kilo de hielo que se sumergía en agua a 20 °C. Entre las respuestas de los alumnos se encontraban alguna que decía que tardaba 4 s en fundirse y otra que afirmaba que se necesitaban 11000 años. Ambos extremos son claramente absurdos y deberían haber sido rechazados por los mismos que los obtuvieron. Nunca es un argumento válido “es lo que sale en la calculadora”.

Para juzgar los resultados es conveniente en primer lugar estar familiarizado con los valores típicos de las magnitudes, para tener algún punto de comparación. Lo importante de estos valores típicos no son sus expresiones decimales, sino sus órdenes de magnitud: la potencia de 10 más cercana a ellos.

Una ilustración muy clara de los órdenes de magnitud aplicados a distancia es el documental “potencias de diez”, que ha sido adaptado también en la web.

Así, tendríamos, por ejemplo

Distancia (m)	Sistema típico
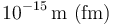
$10^{-15}\,\mathrm{m}\ (\mathrm{fm})$	Núcleo atómico
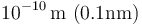
$10^{-10}\,\mathrm{m}\ (0.1\mathrm{nm})$	Átomo
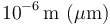
$10^{-6}\,\mathrm{m}\ (\mu\mathrm{m})$	Célula
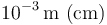
$10^{-3}\,\mathrm{m}\ (\mathrm{cm})$	Hormiga
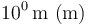
$10^0\,\mathrm{m}\ (\mathrm{m})$	Ser humano
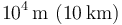
$10^4\,\mathrm{m}\ (10\,\mathrm{km})$	Sevilla
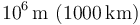
$10^6\,\mathrm{m}\ (1000\,\mathrm{km})$	España
$10^7\,\mathrm{m}\ (10000\,\mathrm{km})$	Tierra
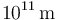
$10^{11}\,\mathrm{m}$	Distancia Tierra-Sol
$10^{16}\,\mathrm{m}$	Distancia a Alfa Centauri
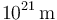
$10^{21}\,\mathrm{m}$	Tamaño de la Vía Láctea

Al pasar de un orden de magnitud al siguiente estamos multiplicando por 10 los rangos de las magnitudes. Así, para distancias, tenemos distancias “del orden del cm”, “del orden del mm”. etc.

Las magnitudes físicas cuyos valores abarcan muchos órdenes de magnitud suelen representarse en una escala en la que la distancia entre órdenes de magnitud sucesivos es siempre la misma. Un ejemplo típico de esto es la descripción del espectro electromagnético

Las escalas de este tipo se denomina logarítmicas, porque lo que está equiespaciado no son las distancias, sino sus logaritmos. Así midiendo todas las distancias en metros, un mm tiene logaritmo decimal -3, un cm -2, un km +3 y así sucesivamente. De un orden de magnitud al siguiente el logaritmo decimal aumenta en una unidad.

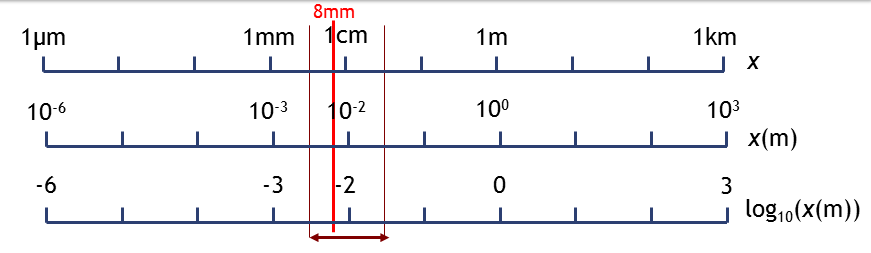
La frontera entre órdenes de magnitud sucesivos no están definidas de forma tajante. Sin embargo, al hablar de una distancia de 8mm, por ejemplo, ¿diríamos que es del orden del mm o del cm? Aunque se mida en mm, su valor nos inclinaría a considerarla del orden del cm, que está más cerca. ¿Qué significa en este contexto “más cerca”? Podemos definirlo como que se encuentra a menos de medio órden de magnitud de la unidad más próxima. Considerando que estamos trabajando con logaritmos, sería

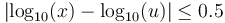
$\left|\log_{10}(x) - \log_{10}(u)\right| \leq 0.5$

o, equivalentemente

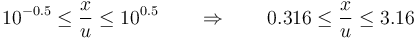
$10^{-0.5}\leq \frac{x}{u}\leq 10^{0.5}\qquad \Rightarrow\qquad 0.316 \leq \frac{x}{u}\leq 3.16$

Puesto que las fronteras no son precisas, podemos decir que entre 0.3mm y 3mm consideraremos la distancia del orden del mm, entre 3mm y 3cm del orden del cm y así sucesivamente.

5 Estimaciones

Además de conocer valores típicos, conviene hacer estimaciones respecto al orden de magnitud de los resultados. Estas estimaciones no se obtienen resolviendo exactamente el problema, sino a partir de aproximaciones razonables y operaciones sencillas (usualmente multiplicaciones y divisiones).

Por ejemplo, si nos preguntamos ¿cuántos pelos tiene una persona en su cabeza, en promedio? ¿Cuál sería el orden de magnitud del resultado? ¿Diez mil, cien mil, un millón, diez millones? Podemos estimarlo de esta forma: los cabellos crecen sobre un casquete aproximadamente semiesférico, de circunferencia unos 60 cm. La densidad de cabellos en este casquete no es uniforme, pero visualizando un cm² de piel, podemos estimar que el número de cabellos que parten de él es del orden de 100 (probablemente algo menos, pero eso no afecta al orden de magnitud). Por tanto

$N \sim (2\pi R^2) d = \frac{L^2}{2\pi} d = \frac{(60\,\mathrm{cm})^2}{6.28}\,\frac{100\,\mathrm{pelos}}{1\,\mathrm{cm}^2}\sim 10^5\,\mathrm{pelos}$

Esto es una estimación, claro está, y el número exacto para cada persona podrá ser menor o mayor, pero del mismo orden. Lo que está claro es que no tenemos un millón de pelos (que implicaría unos 1000 cabellos por cm² lo que es excesivo). Un estudio científico (basado en contar los pelos de una serie de personas, mostró que el valor medio era dependiente del color de los cabellos yendo desde unos 140 000 para los rubios a 90 000 para los pelirrojos, con castaños y morenos en medio).

Medidas, estimaciones e incertidumbres

De Laplace

Contenido

1 Medidas, estimaciones e incertidumbres

2 Cifras significativas

3 Incertidumbres

4 Órdenes de magnitud

5 Estimaciones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES