Medida de la temperatura de un vaso GIA

De Laplace

Contenido 1 Enunciado 2 Solución 2.1 Proceso A 2.2 Proceso B

1 Enunciado

Se quiere determinar la temperatura de un vaso metálico. Para ello, se vierte en él cierto volumen de agua fría a 12 °C y se mide la temperatura de equilibrio, que resulta ser de 20 °C. Se añade un segundo volumen de agua fría igual al primero y se mide la nueva temperatura de equilibrio de 18 °C. ¿Cuál era la temperatura inicial del vaso metálico?

2 Solución

En el ejercicio propuesto se tiene una recipiente o vaso, del cuál se desconocen los valores de su masa m_v, calor específico c_v, y temperatura inicial T. Como el objetivo es determinar esta última y la masa del vaso no va a cambiar, tomaremos como parámetro la capacidad calorífica C_v = m_vc_v del mismo. Por otra parte, para medir la temperatura del vaso se procede a vertir en su interior una cantidad indeterminada de agua, cuya capacidad calorífica C_a = m_ac_a también tendrá un valor desconocido.

La masa de agua está a una temperatura T₁ que, en el escala Celsius, le corresponde un valor de 12°C. Como ésta será, en general, distinta de la temperatura T del vaso, se iniciará un proceso termodinámico (A), que culminará cuando la masa m_a de agua y el vaso se encuentran en desequilibrio térmico. Consideraremos que en dicho proceso sólo va a tener valores significativos la transferencia de energía entre el vaso y la masa de agua, constituyendo ambos el universo observado.

2.1 Proceso A

Como el vaso es un sólido y el agua un fluido incompresible, la única forma posible de transferencia de energía será en forma de calor. Si T₂ es la temperatura de equilibrio al final de este proceso (20°C en la escala Celsius), las cantidades de calor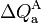 y 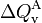transferidas al agua y al vaso serán opuestas:

Por tanto, la variación sufrida por la temperatura del vaso en este proceso sera:

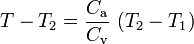
Sin embargo, en esta expresión se desconoce la relación entre las capacidades caloríficas del vaso y de la masa indeterminada de agua. Para ello, debemos realizar un segundo proceso, en el cual hemos de volver a usar una segunda cantidad de agua con igual valor de capaciadad calorífica C_a y, por tanto, con idéntica cantidad de masa m_a. Si esta segunda masa de agua se halla también a 12°C (temperatura T₁), se tendrá de nuevo un desequilibrio térmico, entre ésta y el vaso y el agua del proceso A. Se desencadena, por tanto, un segundo proceso B que finaliza cuando el vaso y la masa 2m_a alcanzan la tempertura de equilibrio T₃ (18°C en la escala Celsius).

2.2 Proceso B

La cantidad de calor transferida en este proceso al sistema, constituido por la segunda masa de agua fría (con igual capacidad calorífica que la primera), es:

Por su parte, la cantidad de calor transferida al entorno (es decir, al conjunto resultante al final del proceso A), será igual a la suma de los calores que se transfieren a la primera cantidad de agua y al vaso:

Exgiendo que los calores transferido a sistema y entorno deben ser opuestos, se obtiene:

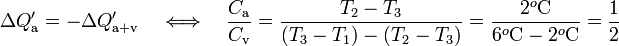
Y sustituyendo este resultado en la expresión del apartado anterior, obtenemos la medida en la escala Celsius de la temperatura inicial del vaso: