Mecánica del sólido rígido (CMR)

De Laplace

1 Introducción

La mecánica del sólido rígido se apoya en la mecánica de los sistemas de partículas y en este sentido no aporta leyes físicas nuevas. No obstante, el modelo del sólido rígido aporta importantes consecuencias tanto teóricas como prácticas.

Para estudiar el comportamiento de los sólidos es conveniente estructurar la materia en cuatro partes (cada una de las cuales se puede subdividir a su vez):

• Cinemática
• Cinética y geometría de masas
• Estática
• Dinámica

2 Concepto de sólido rígido

2.1 Compresibilidad nula

Prácticamente todos los sistemas de la naturaleza se pueden tratar como sistemas de partículas. Sin embargo, cuando los sistemas incluyen un número excesivo de partículas (del orden del número de Avogadro), resulta impracticable el tratarlo como agregados de partículas individuales, tanto por la complejidad matemática que implica, como por el hecho de que se desconoce la mayor parte de la información relevante (posiciones y velocidades de todas y cada una de las partículas, así como las leyes de fuerzas con la que interactúan).

Por ello, se renuncia a una descripción microscópica y se elabora modelos macróscopicos mucho más sencillos y de experimentación directa. Los sistemas macroscópicos suelen clasificarse en diferentes estados de la materia: sólidos, líquidos, gases y plasmas. De estos, los tres últimos se agrupan conjuntamente en el concepto de fluidos, por oposición a los sólidos.

La diferencia entre un fluido y un sólido es que mientras el fluido se adapta a la forma del recipiente que lo contiene, el sólido no lo hace. También se distinguen en su comportamiento cuando se ejerce una fuerza tangente a su superficie (fuerza de cizalla). Un fluido adquiere una velocidad en la dirección de la fuerza (velocidad dependiente de la viscosidad del fluido), mientras que un sólido se deforma en dicha dirección.

Todos los sólidos son deformables cuando se aplica una fuerza sobre ellos, y el grado con que lo hacen se mide por su elasticidad. En el caso de un resorte, esta deformabilidad se mide con la constante de recuperación que aparece en la ley de Hooke.

Cuanto menor es la compresibilidad de un sólido (o mayor su constante de recuperación) más indeformable es, más fuerza es necesaria para conseguir una dilatación dada. Por ejemplo, de acuerdo con la ley de Hooke, la dilatación de un resorte viene dada por

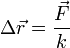
cuando 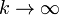la deformación tiende a cero, sea cual sea la fuerza aplicada.

Un primer estudio de los sólidos consiste, por tanto, en hacer el modelo de sólido completamente indeformable, o sólido rígido.

2.2 Extensión indefinida

Todo sólido real está formado por un gran número de partículas materiales que ocupan una extensión finita en el espacio y poseen, en conjunto, una forma definida. Habrá puntos del espacio que estarán ocupados por alguna partícula material y habrá puntos en los que no habrá partícula alguna, bien porque se hallen en el exterior del sólido real, bien porque se encuentren en los intersticios entre las partículas materiales.

Sin embargo, desde el punto de vista del análisis de las velocidades y aceleraciones de un sólido, objeto de este tema, no necesitamos considerar este tamaño finito, ni la forma de los sólidos. Podemos suponer un sólido ideal extendido a todo el espacio, cuya distribución de velocidades es la correspondiente al sólido real que estemos estudiando. Al aplicar este sólido ideal a un caso concreto, basta tener en cuenta que para aquellos puntos exteriores (o interiores) al sólido en los que no hay partículas de este, no tiene sentido asignarles una velocidad.

Un sólido ideal queda entonces identificado por un cierto sistema de referencia, y cada punto del espacio, sean cuales sean sus coordenadas, puede tratarse como parte del sólido.

3 Condición de rigidez

3.1 Condición geométrica

Matemáticamente, un sólido rígido se caracteriza por ser un sistema de partículas tal que la distancia entre cada par de partículas que lo componen permanece constante en cada momento

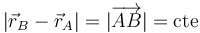
Esta es la condición geométrica de rigidez.

Puesto que se aplica a cada par de partículas supone N(N − 1) / 2 vínculos geométricos (tantos como el número de pares de partículas), si bien muchos de ellos son redundantes.

3.2 Condición cinemática

Cada ligadura geométrica implica una relación entre las velocidades posibles, ya que si la distancia entre un par de partículas es constante, no puede ser que sus velocidades nos digan que se están acercando o alejando. Obtenemos estas relaciones derivando en la expresión de los vínculos geométricos.

Elevando al cuadrado

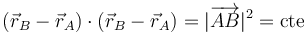
y derivando esta expresión respecto al tiempo obtenemos la condición sobre las velocidades.

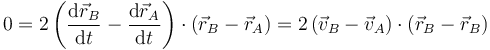
Esta es la condición cinemática de rigidez,

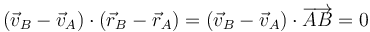
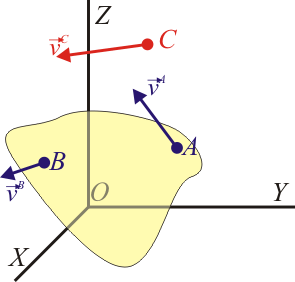
Esta condición nos dice que la velocidad relativa del punto B respecto del A (esto es, la que mide un observador situado en A y moviéndose con este punto) es ortogonal al vector de posición relativa

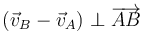
Esta condición cinemática se puede visualizar. Si estamos solidariamente unidos al punto A, vemos al punto B siempre a la misma distancia, es decir, se encuentra sobre la superficie de una esfera imaginaria. Al moverse sobre la esfera, su velocidad es tangente a la superficie y perpendicular al radio, que es el vector de posición relativo. Por tanto la velocidad relativa y la posición relativa son ortogonales.

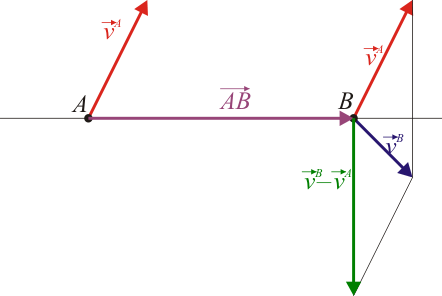
La condición cinemática la podemos escribir también como

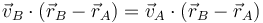
o, empleando el vector de posición relativo

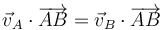
Introduciendo el vector unitario en la dirección del segmento que une los dos puntos y en el sentido de la partícula A a la B.

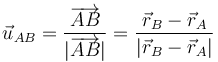
queda

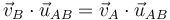
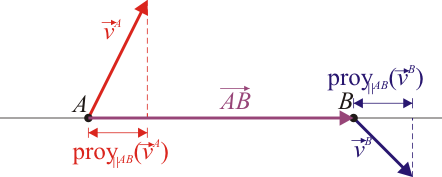
siendo cada miembro la proyección de la velocidad en la dirección del vector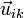

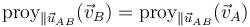
La condición cinemática de rigidez implica que, dadas dos partículas, A y B, la proyección de sus respectivas velocidades sobre la recta que las une es la misma. Por ello se dice que el campo de velocidades es equiproyectivo.

El que las dos proyecciones sean iguales quiere decir que la componente de las velocidades en esa dirección es la misma; las dos partículas avanzan o retroceden a lo largo de esa línea en igual medida, manteniendo su distancia relativa.

4 Grados de libertad

El número de grados de libertad de un sistema se define como el número de coordenadas del sistema menos el número de ecuaciones de vínculos independientes que relacionan dichas coordenadas. En muchos casos el número de grados de libertad equivale al número de variables necesarias para describir el movimiento del sistema.

¿Cuántos grados de libertad tiene un sólido rígido? El número de coordenadas es 3N, siendo N el número de partículas. En un sólido macroscópico este número es gigantesco, pero es claro que para describir el movimiento de un sólido no necesitamos tantas variables, ya que la condición de rigidez impone muchos vínculos.

Para ver el número de variables necesarias consideramos primero una sola partícula. Para dar su posición necesitamos 3 variables, por ejemplo, sus coordenadas cartesianas.

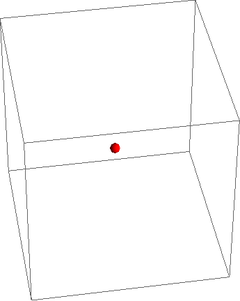
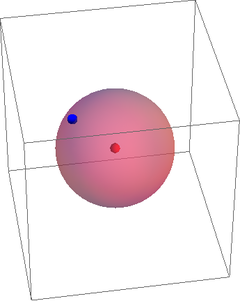
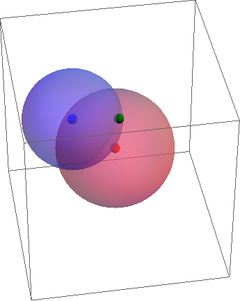
Situamos ahora una segunda partícula. Su posición tiene 3 coordenadas, pero una de ellas es conocida, ya que sabemos que la distancia a la primera partícula es constante. La posición de la segunda partícula se encuentra sobre una esfera de radio d₁₂ alrededor de la primera y para dar una posición sobre una esfera solo necesitamos 2 variables (latitud y longitud, por ejemplo).

Una tercera partícula se encuentra a una distancia d₁₃ de la primera y a una distancia d₂₃ de la segunda. La posición de esta tercera partícula se encuentra por tanto sobre la circunferencia intersección de una esfera de radio d₁₃ alrededor de la primera y una esfera de radio d₂₃ alrededor de la segunda, y para localizar una posición concreta sobre una circunferencia solo necesitamos 1 variable.

Para una cuarta y siguientes, la distancia a las tres primeras nos define de forma unívoca su posición, por lo que no precisamos variables adicionales.

Por tanto, el número de grados de libertad de un sólido rígido es 3+2+1 = 6. Dando seis datos, que pueden ser diferentes según las circunstancias, podemos describir de manera completa la posición de un sólido rígido.

Una forma alternativa de comprobar que un sólido rígido tiene 6 grados de libertad consiste en pensar que la posición del sólido queda unívocamente determinada conocidas las posiciones de tres puntos no alineados del mismo. Tres puntos se describen mediante un total de 9 coordenadas (por ejemplo, 3 x 3 coordenadas cartesianas), pero esas 9 coordenadas no son independientes ya que deben satisfacer 3 ecuaciones de ligadura: las ecuaciones que establecen las distancias relativas constantes entre dichos puntos. Por tanto, el número de grados de libertad del sólido se reduce a 9 − 3 = 6.