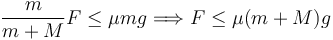Masas deslizando sobre un plano horizontal, Noviembre 2014 (G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Análisis del movimiento
- 2.2 Condición sobre el coeficiente de rozamiento

1 Enunciado

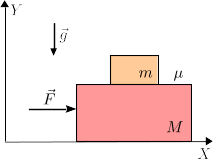
Las dos masas de la derecha se mueven horizontalmente. El contacto de la masa $M$ sobre el suelo es liso, mientras que el contacto entre las dos masas es rugoso con un coeficiente de rozamiento estático $μ$ . Una fuerza $\vec{F}$ horizontal actúa sobre la masa $M$ .

Si durante el movimiento las dos masas mantienen su posición relativa, ¿cuál es su aceleración?
Calcula la fuerza total que la masa $m$ ejerce sobre la masa $M$ .
¿Qué condición debe cumplir 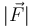$|\vec{F}|$ para que la masa $m$ no deslice respecto de la masa $M$ ?

2 Solución

2.1 Análisis del movimiento

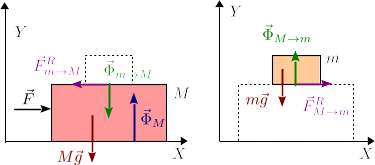
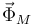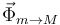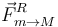La figura muestra las fuerzas que actúan sobre cada una de las masas. Sobre $M$ actúa su peso, la fuerza $\vec{F}$ , la fuerza de reacción vincular del plano horizontal $\vec{\Phi}_M$ , y la fuerza que ejerce sobre ella la masa $m$ . Esta tiene dos componentes, una normal $\vec{\Phi}_{m\to M}$ y otra tangencial debida al rozamiento $\vec{F}^R_{m\to M}$ .

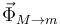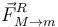Sobre la masa $m$ actúa su peso y la fuerza que ejerce sobre ella la masa $M$ , que a su vez tiene una componente vertical $\vec{\Phi}_{M\to m}$ y $\vec{F}^R_{M\to m}$ . Por la tercera de Newton sabemos que

$\vec{\Phi}_{M\to m} = -\vec{\Phi}_{m\to M}, \qquad \vec{F}^R_{M\to m} = -\vec{F}^R_{m\to M}$

Vamos a expresar las fuerzas en el sistema de ejes de la figura. Para la masa $M$ tenemos

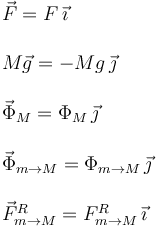
$\begin{array}{l} \vec{F} = F\,\vec{\imath}\\ \\ M\vec{g} = -Mg\,\vec{\jmath} \\ \\ \vec{\Phi}_M = \Phi_M\,\vec{\jmath}\\ \\ \vec{\Phi}_{m\to M} = \Phi_{m\to M}\,\vec{\jmath}\\ \\ \vec{F}^R_{m\to M} = F^R_{m\to M}\,\vec{\imath} \end{array}$

Para la masa $m$ tenemos

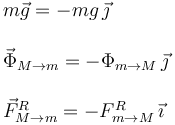
$\begin{array}{l} m\vec{g} = -mg\,\vec{\jmath}\\ \\ \vec{\Phi}_{M\to m} = -\Phi_{m\to M}\,\vec{\jmath}\\ \\ \vec{F}^R_{M\to m} = -F^R_{m\to M}\,\vec{\imath} \end{array}$

En la expresión de las fuerzas sobre $m$ ya hemos utilizado la Tercera Ley de Newton. La condición para que las masas mantengan su posición relativa es que se muevan con la misma aceleración, es decir

$\begin{array}{ll} M\vec{a} = \vec{F} + M\vec{g} + \vec{\Phi}_M + \vec{\Phi}_{m\to M} + \vec{F}^R_{m\to M} & \to \left\{ \begin{array}{ll} (X): & Ma = F + F^R_{m\to M}\\ (Y): & 0 = -Mg + \Phi_M + \Phi_{m\to M} \end{array} \right. \\ &\\ m\vec{a} = m\vec{g} + \vec{\Phi}_{M\to m} + \vec{F}^R_{M\to m} & \to \left\{ \begin{array}{ll} (X): & ma = -F^R_{m\to M}\\ (Y): & 0 = -mg - \Phi_{m\to M} \end{array} \right. \end{array}$

Tenemos cuatro ecuaciones para cuatro incógnitas, a saber, 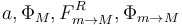$a, \Phi_M, F^R_{m\to M}, \Phi_{m\to M}$

Sumando la primera y la tercera ecuaciones tenemos

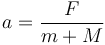
$a = \dfrac{F}{m+M}$

Sumando la segunda y la cuarta ecuaciones tenemos

$Φ M = (m + M) g$

De la tercera ecuación obtenemos

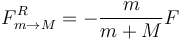
$F^R_{m\to M} = -\dfrac{m}{m+M}F$

Y de la cuarta ecuación obtenemos

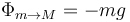
$\Phi_{m\to M} = -mg$

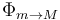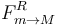Los signos de $\Phi_{m\to M}$ y $F^R_{m\to M}$ indican que el sentido de las fuerzas en el diagrama de cuerpo libre es el correcto. La fuerza total que $m$ ejerce sobre $M$ es

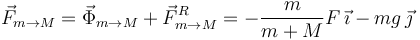
$\vec{F}_{m\to M} = \vec{\Phi}_{m\to M} + \vec{F}^R_{m\to M} = -\dfrac{m}{m+M}F\,\vec{\imath} - mg\,\vec{\jmath}$

Esta fuerza apunta hacia abajo y la izquierda, y su módulo es

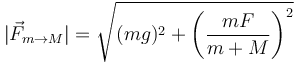
$|\vec{F}_{m\to M}| = \sqrt{(mg)^2 + \left(\dfrac{mF}{m+M}\right)^2}$

Podemos comprobar que cuando $m = 0$ esta fuerza se anula, como es lógico.

2.2 Condición sobre el coeficiente de rozamiento

La masa $m$ no desliza sobre $M$ debido al rozamiento. Para que esto ocurra el módulo de la fuerza de rozamiento sobre ella no debe exceder su valor máximo, es decir

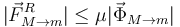
$|\vec{F}^R_{M\to m}| \leq \mu|\vec{\Phi}_{M\to m}|$

Esta condición se traduce en

$\dfrac{m}{m+M}F \leq \mu mg \Longrightarrow F\leq \mu(m+M)g$

Masas deslizando sobre un plano horizontal, Noviembre 2014 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Análisis del movimiento

2.2 Condición sobre el coeficiente de rozamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES