Masa que cuelga de un cilindro con pistón (GIE)
De Laplace
1 Enunciado
Se tiene un tubo hermético, de 16cm² de sección, cerrado por un émbolo móvil. Las paredes y el émbolo están aislados térmicamente del exterior. En el interior del tubo hay aire seco (γ=1.4). El tubo se halla en posición vertical, con el émbolo en su parte inferior. Inicialmente el émbolo se encuentra a 10cm de la base, estando el aire interior a 15°C y 100kPa, que también son la temperatura y presión exterior. En ese momento se cuelga del émbolo un saco de harina de 35N de peso, de manera que el émbolo desciende bruscamente. Halle
- La presión, temperatura y volumen del gas interior en la nueva posición de equilibrio.
- El trabajo realizado sobre el gas en este proceso.
- La variación de entropía del gas en el proceso.
Suponga ahora que el saco de harina tiene un pequeño orificio por el que se escapa lentamente la harina hasta vaciarse por completo (despreciamos el peso del propio saco). Halle
- La presión, temperatura y volumen del gas interior en la posición final de equilibrio.
- El trabajo realizado sobre el gas en este proceso.
- La variación de entropía del gas en este proceso.
Dato: Constante universal de los gases ideales 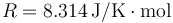
2 Expansión brusca
Este problema es como el de Trabajo_en_una_compresión_por_un_peso solo que ahora en lugar de ser una compresión es una expansión adiabática.
- Presión
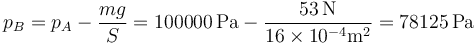
- Volumen
- Por ser adiabático

Lo que da
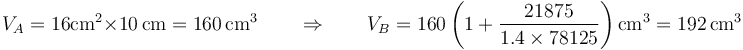
- Temperatura
- por la ley de los gases ideales

- Trabajo
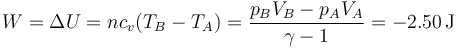
- Variación de entropía
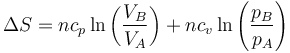
donde

y queda
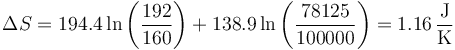
3 Compresión cuasiestática
- Presión
La final es la misma que la inicial
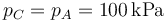
- Volumen
- La compresión es adiabática y cuasiestática, por lo que se cumple la ley de Poisson

- Temperatura
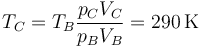
- Trabajo
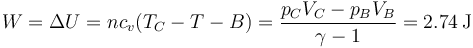
- Entropía
- Por ser adiabático y cuasiestático