Masa que cuelga de dos poleas

De Laplace

1 Enunciado

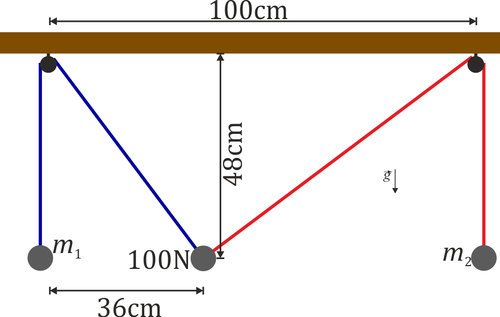
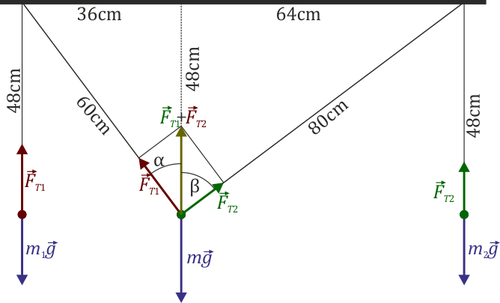
Un bloque con un peso de 100 N cuelga de dos hilos que pasan por sendas poleas ideales colgadas del techo y separadas 100 cm. En los otros extremos de los hilos cuelgan masas m₁ y m₂. En el equilibrio, la masa central se halla a 36 cm en la horizontal de la primera polea y 48 cm en la vertical. Las otras dos masas se encuentran a la misma altura respecto al techo.

1. Calcule los pesos de las dos masas de los extremos que garantizan que el sistema está en equilibrio.
2. Supongamos que agarramos la masa central y la desplazamos lentamente 28 cm hacia la derecha, sujetándola en la nueva posición. ¿Qué fuerza extra debe hacerse sobre la masa central para mantener el sistema quieto en esa posición?
3. ¿Qué trabajo hay que realizar para llevar a cabo el desplazamiento anterior?

Dato:

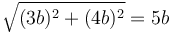
2 Pesos en equilibrio

Si la masa central está en equilibrio es porque

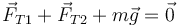
Separando en componentes, nos quedan las ecuaciones

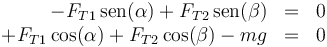
siendo α y β los ángulos que cada hilo forma con la vertical.

Estos ángulos verifican

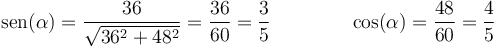
y

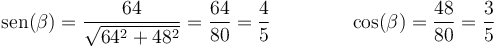
Por tanto, tenemos el sistema (multiplicando por 5)

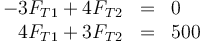
con solución

También se puede llegar a este resultado observando que los dos hilos son ortogonales y proyectando 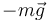sobre ellos (salvo un factor, esto es lo mismo que ocurre en otro problema.

Puesto que las tres masas están en equilibrio, la tensión de cada hilo equivale al peso de la masa que cuelga de él. Por tanto

3 Fuerza en la nueva posición

Cuando la masa central se desplaza 28  pasa a estar a 64 cm en horizontal de polea de la izquierda. Es decir, su posición es la simétrica de la anterior y los ángulos α y β han intercambiado sus valores.

Sin embargo, esta posición no es de equilibrio, ya que aunque ha cambiado de posición, las tensiones no se han modificado (ya que las otras dos masas siguen pesando lo mismo). Por tanto, es necesario una fuerza adicional, 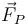, para que se quede inmóvil.

Incluyendo esta fuerza, quedan las ecuaciones

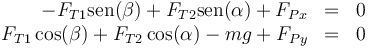
Despejamos y sustituimos

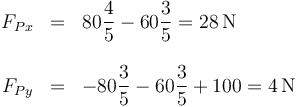
o, en forma vectorial,

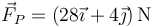
Esta fuerza es tal que, sumada con las dos tensiones, debe anular al peso.

4 Trabajo necesario

Este es un sistema conservativo, ya que no hay rozamiento en ningún punto.

Por tanto, todo el trabajo que se realiza sobre el sistema se emplea en aumentar la energía potencial (es decir, se emplea en aumentar la energía cinética que, como el sistema finalmente se para sin rozamiento, se transforma en energía potencial).

¿Cuánto cambia la energía potencial? Parecería que nada, pues la masa central se mueve horizontalmente, pero no es así. Al moverse la masa central tira de los hilos, y como resultado la masa 1 asciende 20cm (ya que la distancia de m a la polea pasa de 60  a 80 cm) y la masa 2 desciende otros 20.

Por tanto