De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

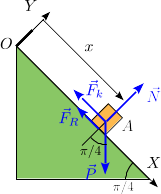
Una masa m está conectada a un muelle de constante elástica k y longitud natural nula. La masa puede deslizarse por un plano inclinado como se indica en la figura. El muelle se mantiene siem- pre paralelo a la superficie del plano inclinado. La gravedad actúa como se indica en el dibujo.

Si el contacto entre la masa y el plano es liso, ¿para que valor de x la masa está en equilibrio?
Teniendo en cuenta ahora el rozamiento y suponiendo que 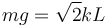$mg=\sqrt{2}kL$ , ¿cuál es el rango de posiciones de equilibrio?

2 Solución

2.1 Fuerzas sobre la masa

La figura de la derecha muestra las fuerzas que actúan sobre la masa: su peso, la fuerza del muelle, la normal del plano y la fuerza de rozamiento. El sentido de todas es conocido, salvo la de rozamiento. La expresión de estas fuerzas es

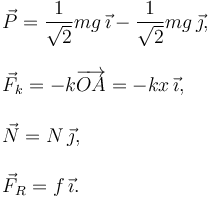
$\begin{array}{l} \vec{P} = \dfrac{1}{\sqrt{2}}mg\,\vec{\imath} -\dfrac{1}{\sqrt{2}}mg\,\vec{\jmath},\\ \\ \vec{F}_k = -k\overrightarrow{OA} = -kx\,\vec{\imath},\\ \\ \vec{N} = N\,\vec{\jmath},\\ \\ \vec{F}_R = f\,\vec{\imath}. \end{array}$

Como el vínculo impuesto por el plano inclinado es bilateral debe cumplirse $N > 0$ .

2.2 Equilibrio sin rozamiento

Si suponemos que no hay rozamiento la condición de equilibrio es

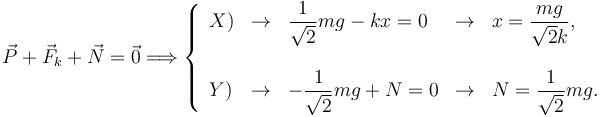
$\vec{P} + \vec{F}_k + \vec{N}=\vec{0} \Longrightarrow \left\{ \begin{array}{lclcl} X) & \to & \dfrac{1}{\sqrt{2}}mg - kx = 0 & \to & x = \dfrac{mg}{\sqrt{2}k},\\ \\ Y) & \to & -\dfrac{1}{\sqrt{2}}mg + N = 0 & \to & N = \dfrac{1}{\sqrt{2}}mg. \end{array} \right.$

2.3 Equilibrio con rozamiento

Si suponemos que ahora hay rozamiento, y ademas imponemos que 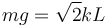$mg=\sqrt{2}kL$ , la condición de equilibrio es

$\vec{P} + \vec{F}_k + \vec{N} + \vec{F}_R=\vec{0} \Longrightarrow \left\{ \begin{array}{lcl} X) & \to & kL - kx + f = 0,, \\ Y) & \to & -kL + N = 0. \end{array} \right.$

De la primera expresión obtenemos que, para que haya equilibrio, la fuerza de rozamiento y la fuerza normal del plano deben valer

$\vec{N} = kL\,\vec{\jmath}, \qquad\qquad \vec{F}_R = k(x-L)\,\vec{\imath}.$

Para que el equilibrio sea posible el módulo de la fuerza de rozamiento debe ser menor que el valor máximo posible

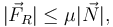
$|\vec{F}_R| \leq \mu |\vec{N}|,$

siendo $μ$ el coeficiente de rozamiento estático. Hemos de considerar dos situaciones

$x > L$

En este caso el módulo de la fuerza de rozamiento es

$|\vec{F}_R| = k|x-L| = k(x-L) \leq \mu kL \Longrightarrow x\leq L\,(1+\mu).$

$x < L$

En este caso el módulo de la fuerza de rozamiento es

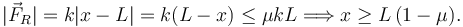
$|\vec{F}_R| = k|x-L| = k(L-x) \leq \mu kL \Longrightarrow x\geq L\,(1-\mu).$

Por tanto, para que el equilibrio sea posible debe ocurrir

$x\in [L(1-\mu), \, L(1+\mu)].$

Masa en plano inclinado con muelle (Nov. 2018 G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas sobre la masa

2.2 Equilibrio sin rozamiento

2.3 Equilibrio con rozamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES