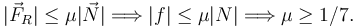De Laplace

1 Enunciado

Una partícula de masa m está obligada a moverse a lo largo de un hilo delgado circular de radio R, como se indica a la figura. La partícula está conectada a un muelle de constante elástica k y longitud natural nula. El punto de anclaje A del muelle puede moverse sobre el eje OY, de modo que el muelle siempre permanece horizontal. El contacto entre la partícula y el hilo es rugoso, con coeficiente de rozamiento estático μ.

1. Dibuja el diagrama de fuerzas de la partícula. Indica de que fuerzas es conocido su sentido antes de resolver el problema
2. ¿Cómo es la fuerza que el muelle ejerce sobre la partícula?. ¿Y la fuerza de rozamiento?
3. Supongamos ahora que se cumple mg = F₀ / 5 y kR = F₀ / 3, siendo F₀ una constante dada. Calcula el módulo de la fuerza normal sobre la partícula en condiciones de equilibrio estático si el ángulo θ es tal que
4. ¿Cuánto debe valer el coeficiente de rozamiento estático para que la situación descrita sea posible?

2 Solución

2.1 Diagrama de fuerzas

La figura de la derecha muestra las fuerzas que actúan sobre la partícula. La fuerza es perpendicular al aro, mientras que la fuerza de rozamiento es tangente al aro. El sentido del peso es hacia abajo. Dado que el muelle tiene longitud natural nula siempre tira hacia el punto A. Entonces la normal siempre va hacia fuera. El sentido de la fuerza de rozamiento depende de donde esté la partícula, es decir, no es conocido a priori.

2.2 Expresión de las fuerzas

Observando los ángulos en la figura previa tenemos que la expresión de las fuerzas en el sistema de ejes de la figura es

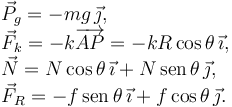
2.3 Situación de equilibrio estático

La situación de equilibrio estático se obtiene imponiendo que la suma de fuerzas sobre la partícula sea nula

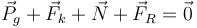
Obtenemos así dos ecuaciones escalares, una por cada componente

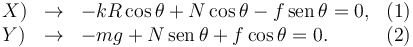
Introduciendo los valores de mg, kR y θ que se dan en el enunciado estas ecuaciones quedan

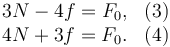
Resolviendo tenemos

2.4 Condición sobre el coeficiente de rozamiento estático

Para que no haya deslizamiento debe ocurrir