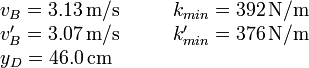Entrar Página Discusión Historial Go to the site toolbox

Masa deslizando por una pendiente hacia un muelle (GIA)

De Laplace

Contenido

1 Enunciado

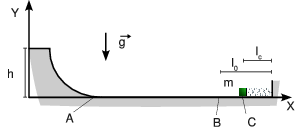
Una masa m se encuentra al borde de una pendiente. Después de la pendiente se extiende una llanura, al final de la cual hay un muelle relajado de constante elástica k y longitud natural l0. La masa se encuentra a una altura h relativa al muelle. Suponemos que no existe fuerza de rozamiento entre la masa y la superficie.

  1. Determina la velocidad con la que la masa impacta en el muelle (punto B).
  2. ¿Cuál es el valor mínimo de la constante elástica del muelle, kmin, para que este pueda evitar que la masa toque la pared?
  3. Supón ahora que entre los puntos A y B hay una región de longitud d en la que existe rozamiento entre la masa y el suelo. Si el coeficiente de rozamiento es μ, ¿cuál es el nuevo valor mínimo de k en el apartado anterior?
  4. Supongamos que k > kmin. En la situación de rozamiento del apartado anterior, calcula la velocidad con la que la partícula vuelve al punto A y la altura a la que sube por la pendiente.
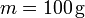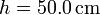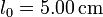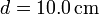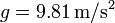  5. Calcula numéricamente las magnitudes pedidas si m=100\,\mathrm{g}, h=50.0\,\mathrm{cm}, l_0=5.00\,\mathrm{cm}, μ = 0.200, d=10.0\,\mathrm{cm}, g=9.81\,\mathrm{m/s^2}.

2 Solución

2.1 Velocidad en B

En su trayecto desde el punto inicial hasta el punto B la partícula está sometida a dos fuerzas, la de la gravedad y la fuerza de reacción vincular del suelo sobre ella. El enunciado dice que no hay rozamiento, por lo que la f.r.v. es siempre perpendicular al deslizamiento y no realiza trabajo. La fuerza de la gravedad es conservativa, es decir, se puede definir una energía potencial para la partícula asociada a la acción de la gravedad. Tomando como referencia de energía potencial la altura de la llanura, la energía potencial es

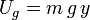
U_g = m\,g\,y

siendo y la altura de la masa sobre la llanura.

Entonces, en el trayecto de la partícula hasta el punto B se puede definir una energía mecánica que se conserva. Esa energía mecánica es

E = T(y) + U(y) = \frac{1}{2}mv^2 + mgy

EL valor de E es constante. Para calcular su valor necesitamos saber cuanto valen la energía cinética y potencial en un punto. Nos dicen que la partícula parte del reposo, luego en el instante inicial T = 0. Como también nos dan su altura inicial tenemos

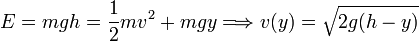
E = mgh = \frac{1}{2}mv^2+mgy \Longrightarrow v(y) = \sqrt{2g(h-y)}

Para el punto B tenemos y = 0. Por tanto la velocidad en B es

v_B = \sqrt{2gh}

2.2 Compresión del muelle

Al llegar a B hay otra fuerza más que actúa sobre la partícula, la del resorte. Esta también es conservativa, por lo que se le puede asignar una energía potencial y la energía mecánica correspondiente se conserva. La energía potencial del muelle es

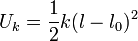
U_k = \frac{1}{2}k(l-l_0)^2

donde l es la elongación del muelle y l0 es su elongación natural. Cuando llega la partícula l = l0, con lo cual la energía potencial en ese instante es cero. Por tanto, la energía mecánica en B es

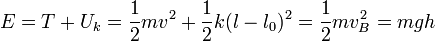
E = T + U_k = \frac{1}{2}mv^2+\frac{1}{2}k(l-l_0)^2= \frac{1}{2}mv_B^2 = mgh

La partícula comprime el muelle y este la va frenando. De este modo, la energía cinética de la masa se convierte en energía potencial elástica. Si llamamos C al punto en el que la masa se detiene, para ese punto T = 0, y por tanto

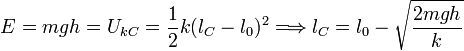
E = mgh = U_{kC} = \frac{1}{2}k(l_C-l_0)^2 \Longrightarrow l_C = l_0 - \sqrt{\frac{2mgh}{k}}

Escogemos el signo menos en la raíz porque el muelle se comprime. Si se estirase habría que escoger el signo positivo.

Para que la partícula se frene antes de llegar a la pared debe cumplirse

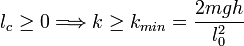
l_c\geq 0 \Longrightarrow k\geq k_{min}=\frac{2mgh}{l_0^2}

2.3 Efecto del rozamiento

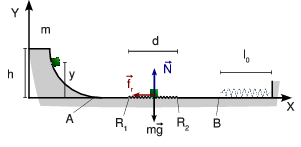
Tenemos el mismo problema, pero ahora hay una región entre A y B donde actúa una fuerza de rozamiento, con coeficiente de rozamiento dinámico μ. Como esta fuerza de rozamiento es no conservativa, la energía mecánica no se conserva. Pero en este caso simple podemos calcular cuanto cambia. La variación de la energía mecánica es igual al trabajo realizado por la fuerza no conservativa, la de rozamiento en este caso

ΔE = Wroz

Estamos interesados en el trayecto hasta B. La fuerza de rozamiento actúa sólo en la zona delimitada por los puntos R1 y R2. El trabajo que realiza es

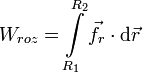
W_{roz} = \int\limits_{R_1}^{R_2}\vec{f}_r\cdot\mathrm{d}\vec{r}

Como está en movimiento, el módulo de la fuerza de rozamiento es igual al coeficiente de rozamiento por el módulo de la normal. A su vez, éste es igual al peso de la partícula. Además, la fuerza de rozamiento se opone al movimiento que en este caso es hacia la derecha. Tenemos

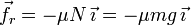
\vec{f}_r = -\mu N\,\vec{\imath} = -\mu mg\,\vec{\imath}

En la zona donde el rozamiento actúa la partícula se mueve a lo largo del eje OX. Entonces un desplazamiento infinitesimal puede escribirse como

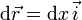
\mathrm{d}\vec{r} = \mathrm{d} x\,\vec{i}

Con esto el trabajo de la fuerza de rozamiento es

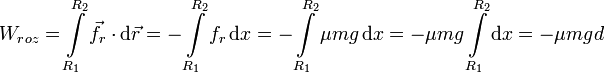
W_{roz} = \int\limits_{R_1}^{R_2}\vec{f}_r\cdot\mathrm{d}\vec{r} = -\int\limits_{R_1}^{R_2}f_r\,\mathrm{d} x = -\int\limits_{R_1}^{R_2}\mu mg\,\mathrm{d} x= -\mu mg\int\limits_{R_1}^{R_2}\mathrm{d} x = -\mu mgd

La energía mecánica en A es la misma que en el instante inicial. En el trayecto hasta B actúa la fuerza de rozamiento. Además en B la energía potencial es cero. Tenemos

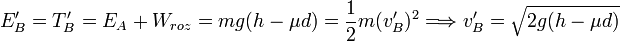
E'_B = T'_B = E_A + W_{roz} = mg(h-\mu d) = \frac{1}{2}m(v_B')^2 \Longrightarrow v_B' = \sqrt{2g(h-\mu d)}

2.4 Nuevo valor de kmin

Esta parte es igual al segundo apartado. La diferencia es que ahora la energía mecánica en B es la calculada teniendo en cuenta la disminución por el rozamiento. Usando el mismo razonamiento llegamos a

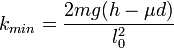
k_{min}=\frac{2mg(h-\mu d)}{l_0^2}

2.5 Altura a la que sube al volver

En su camino de vuelta la partícula sufre otra vez el efecto de la fuerza de rozamiento. Al llegar a A la energía mecánica disminuye otra vez respecto a su valor en B. El trabajo de rozamiento es igual que el calculado antes, pues aunque ahora la masa se desplaza hacia la izquierda, la fuerza de rozamiento apunta hacia la derecha, oponiéndose al movimiento. La energía mecánica en A es

E''A = E'B + Wroz = mg(h − μd) − μmgd = mg(h − 2μd)

La energía en A es puramente cinética. Al subir por la pendiente se va transformando en energía potencial. Cuando la energía potencial se hace cero se para. Si llamamos a este punto D tenemos

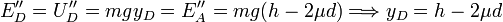
E''_D = U''_D = mgy_D= E''_A = mg(h-2\mu d) \Longrightarrow y_D = h-2\mu d

2.6 Resultados numéricos

Con los datos suministrados los valores son

\left. \begin{array}{lcl} v_B=3.13\,\mathrm{m/s} & \quad & k_{min}=392\,\mathrm{N/m} \\ v'_B=3.07\,\mathrm{m/s} & \quad & k'_{min}=376\,\mathrm{N/m} \\ y_D = 46.0\,\mathrm{cm} && \end{array} \right.
Obtenido de "http://tesla.us.es/wiki/index.php/Masa_deslizando_por_una_pendiente_hacia_un_muelle_(GIA)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:13, 23 ene 2018. - Esta página ha sido visitada 6.289 veces. - Aviso legal - Acerca de Laplace