De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

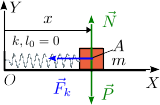
Una masa $m$ puede deslizar sin rozamiento sobre el eje horizontal $O X$ . La masa está conectada a un muelle de constante elástica $k$ y longitud natural $l 0$ . El otro extremo del muelle está conectado al origen de coordenadas. Determina el movimiento $x (t)$ de la masa en estos tres casos:

Se suelta la masa desde el origen con velocidad nula.
Se suelta la masa desde la posición de equilibrio con velocidad $v 0$ .
Se suelta la masa desde la posición $x 0$ con velocidad $v 0$ .

2 Solución

2.1 Ecuación de movimiento

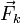Las fuerzas que actúan sobre la masa son su peso $\vec{P}$ , la fuerza ejercida por el muelle, $\vec{F}_k$ y la fuerza vincular de la superficie horizontal de la superficie sobre la masa, $\vec{N}$ . La ecuación diferencial del movimiento es proporcionada por la Segunda Ley de Newton

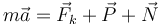
$m\vec{a} = \vec{F}_k + \vec{P} + \vec{N}$

Escogemos el eje $X$ paralelo a la superficie y el eje $Y$ perpendicular a ella. Entonces la expresión del término de inercia y las fuerzas es

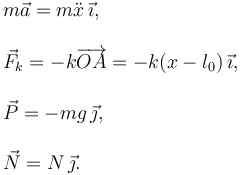
$\begin{array}{l} m\vec{a} = m\ddot{x}\,\vec{\imath},\\ \\ \vec{F}_k = -k\overrightarrow{OA} = -k(x-l_0)\,\vec{\imath},\\ \\ \vec{P} = -mg\,\vec{\jmath},\\ \\ \vec{N} = N\,\vec{\jmath}. \end{array}$

Al aplicar la Segunda Ley obtenemos dos ecuaciones escalares, una por cada componente de la base vectorial

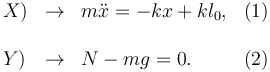
$\begin{array}{lclr} X) & \to & m\ddot{x} = -kx + kl_0, & (1)\\ &&&\\ Y) & \to & N-mg = 0. & (2) \end{array}$

La ecuación (2) nos dice que la fuerza vincular equilibra al peso para que la partícula no atraviese la superficie. Podemos entonces ignorar el peso y la fuerza normal. Si hubiera rozamiento no podríamos hacerlo, pues en régimen dinámico el módulo de la fuerza de rozamiento es proporcional a la normal y no podemos ignorar el valor de esta.

La ecuación (1) es una ecuación diferencial donde la incógnita es $x (t)$ , la coordenada de la partícula sobre el eje $X$ . Vamos a hacer un cambio de variable. Vamos la determinar la posición de la partícula respecto a la posición de equilibrio del muelle. Para ello definimos $s (t)$ de modo que

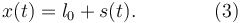
$x(t) = l_0 + s(t). \qquad \qquad (3)$

Cuando $s = 0$ el muelle está relajado y no ejerce fuerza sobre la partícula. Podemos derivar respecto al tiempo a ambos lados de la expresión (3). Teniendo en cuenta que $l 0$ no depende del tiempo obtenemos

$\dot{x} = \dot{s}, \qquad\qquad \ddot{x}=\ddot{s}. \qquad\qquad(4)$

Sustituyendo las expresiones (3) y (4) en la ecuación (1) obtenemos una ecuación diferencial para $s (t)$

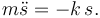
$m\ddot{s} = -k\,s.$

Vamos a pasar $m$ al otro lado

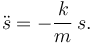
$\ddot{s} = -\dfra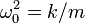c{k}{m}\,s.$

Definimos $\omega_0^2=k/m$ . La ecuación queda

$\ddot{s} = -\omega_0^2s, \qquad\qquad \omega_0=\sqrt{k/m}.$

Obtenemos una ecuación diferencial de segundo orden, porque aparece la derivada segunda de la función incógnita. Esta ecuación es especial y muy importante, por lo que recibe un nombre especial. Es la ecuación de un oscilador armónico, o ecuación del Movimiento Armónico Simple (MAS).

Para que una función verifique la ecuación debe ocurrir que al derivarla dos veces respecto al tiempo el resultado sea la misma función multiplicada por $ω 0$ . Hay dos funciones que cumplen esto: $cos(ω 0 t)$ y $\,\mathrm{sen}\,(\omega_0t)$ . La solución general es una combinación lineal de las dos

$s(t) = A\cos(\omega_0t) + B\,\mathrm{sen}\,(\omega_0t).$

Vamos a comprobar que esta función verifica la ecuación diferencial. Derivando respecto al tiempo obtenemos

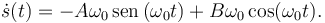
$\dot{s}(t) = -A\omega_0\,\mathrm{sen}\,(\omega_0t) + B\omega_0\cos(\omega_0t).$

Derivando otra vez

$\ddot{s} = -A\omega_0^2\cos(\omega_0t) - B\omega_0^2\,\mathrm{sen}\,(\omega_0t) = -\omega_0^2\,(A\cos(\omega_0t) + B\,\mathrm{sen}\,(\omega_0t)) = -\omega_0^2s(t).$

Efectivamente esta función verifica la ecuación diferencial.

La solución general tiene dos constantes de integración $A$ y $B$ . Desde el punto de vista matemático esto es así porque la ecuación es de segundo orden. Desde el punto de vista físico esto significa que para determinar el movimiento de la partícula necesitamos dos condiciones iniciales: su posición y su velocidad en el instante inicial.

2.2 Caso 1

En este caso la posición y velocidad iniciales de la partícula son

$x(0) = 0, \qquad v(0) = \dot{x}(0) = 0.$

Usando las expresiones (3) y (4) estas condiciones se traducen en las siguientes para $s$

$s(0) = -l_0, \qquad \dot{s}(0) = 0.$

Con el fin de imponer estas condiciones sustituimos $t = 0$ en la solución general $s (t)$ y su derivada 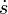$\dot{s}$

$\begin{array}{lcl} \left.\begin{array}{l} s(0) = A\\ s(0) = -l_0 \end{array} \right\} & \to A = -l_0,\\ &&\\ \left.\begin{array}{l} \dot{s}(0) = B\omega_0\\ \dot{s}(0) = 0 \end{array} \right\} & \to B = 0.\\ \end{array}$

Así pues, el movimiento de la partícula en el caso 1 está descrito por la función

$s (t) = - l 0 cos(ω 0 t).$

La coordenada $x$ es

$x(t) = l_0 + s(t) = l_0\,(1-\cos(\omega_0t)).$

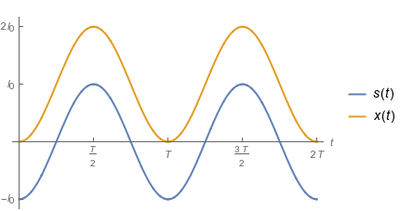
La figura de la derecha muestra las gráficas de $s (t)$ y $x (t)$ . La masa empieza su movimiento en el punto $O$ . Se desplaza hacia la derecha, sobrepasa la posición de equilibrio $s = 0$ , hasta que llega hasta una distancia $l 0$ a la derecha del punto de equilibrio 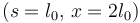$(s=l_0, \, x=2l_0)$ . Ahí da la vuelta hasta que llega a $O$ otra vez y se repite el ciclo. El movimiento es periódico. El período es el tiempo que la partícula tarda en ir y volver al punto $O$ , es decir, el tiempo $T$ para el cual el argumento del coseno es $2π$ . Entonces

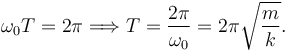
$\omega_0 T = 2\pi \Longrightarrow T = \dfrac{2\pi}{\omega_0} = 2\pi\sqrt{\dfrac{m}{k}}.$

Ese es el período de oscilación de un muelle ideal.

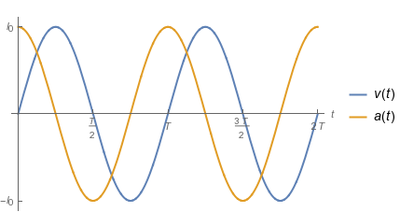
La figura de la derecha muestra la evolución en el tiempo de la velocidad y de la aceleración de la partícula

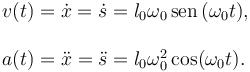
$\begin{array}{l} v(t) = \dot{x} = \dot{s} = l_0\omega_0\,\mathrm{sen}\,(\omega_0 t),\\ \\ a(t) = \ddot{x} = \ddot{s} = l_0\omega_0^2\cos(\omega_0 t). \end{array}$

La rapidez es cero en los puntos extremos del movimiento y es máxima cuando la partícula pasa por el punto de equilibrio del muelle. Por el contrario, la aceleración es máxima en los puntos extremos del movimiento y es cero cuando la posición de la partícula coincide con la de punto de relajación del muelle.

2.3 Caso 2

Tenemos que calcular los valores de las constantes $A$ y $B$ que describen esta situación. Ahora las condiciones iniciales son

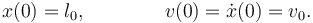
$x(0) = l_0, \qquad \qquad v(0) = \dot{x}(0) = v_0.$

Esto se traduce en estas condiciones iniciales para $s$

$s(0) = 0, \qquad \qquad \dot{s}(0) = v_0.$

Sustituimos $t = 0$ en la solución general $s (t)$ y su derivada 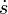$\dot{s}$ e imponemos estas condiciones

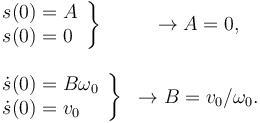
$\begin{array}{lcl} \left.\begin{array}{l} s(0) = A\\ s(0) = 0 \end{array} \right\} & \to A = 0,\\ &&\\ \left.\begin{array}{l} \dot{s}(0) = B\omega_0\\ \dot{s}(0) = v_0 \end{array} \right\} & \to B = v_0/\omega_0.\\ \end{array}$

Entonces la posición de la partícula es descrita por la función

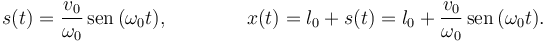
$s(t) = \dfrac{v_0}{\omega_0}\,\mathrm{sen}\,(\omega_0 t), \qquad\qquad x(t) = l_0 + s(t) = l_0 + \dfrac{v_0}{\omega_0}\,\mathrm{sen}\,(\omega_0 t).$

2.4 Caso 3

Ahora las condiciones iniciales son

$x(0) = (x_0+l_0), \qquad \qquad v(0) = \dot{x}(0) = v_0.$

Esto se traduce en estas condiciones iniciales para $s$

$s(0) = x_0, \qquad \qquad \dot{s}(0) = v_0.$

Sustituimos $t = 0$ en la solución general $s (t)$ y su derivada 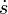$\dot{s}$ e imponemos estas condiciones

$\begin{array}{lcl} \left.\begin{array}{l} s(0) = A\\ s(0) = x_0 \end{array} \right\} & \to A = x_0,\\ &&\\ \left.\begin{array}{l} \dot{s}(0) = B\omega_0\\ \dot{s}(0) = v_0 \end{array} \right\} & \to B = v_0/\omega_0.\\ \end{array}$

Entonces la posición de la partícula es descrita por la función

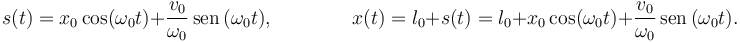
$s(t) = x_0\cos(\omega_0 t) + \dfrac{v_0}{\omega_0}\,\mathrm{sen}\,(\omega_0 t), \qquad\qquad x(t) = l_0 + s(t) = l_0 + x_0\cos(\omega_0 t) + \dfrac{v_0}{\omega_0}\,\mathrm{sen}\,(\omega_0 t).$

En los tres casos la partícula realiza oscilaciones periódicas con período

$T = \dfrac{2\pi}{\omega_0} = 2\pi\sqrt{\dfrac{m}{k}}.$

Masa conectada a un muelle horizontal (GIC)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Ecuación de movimiento

2.2 Caso 1

2.3 Caso 2

2.4 Caso 3

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES