De Laplace

1 Ligaduras

Como hemos visto en el apartado anterior, las restricciones al movimiento en sistemas mecánicos reciben el nombre de ligaduras o vínculos. Hay varias formas de clasificar las ligaduras. En Mecánica Analítica, la distinción mas importante es entre ligaduras holónomas y no holónomas.

1.1 Ligaduras holónomas

Son ligaduras que pueden expresarse por una relación matemática que involucre sólamante las coordenadas geométricas y, quizás, el tiempo. Si el sistema tiene $N$ partículas, la expresión matemática general de una ligadura holónoma es

$f(x_1, x_2, \ldots, x_{3N},t)=0$

Como vemos las velocidades no aparecen en la expresión. Si el tiempo no aparece explícitamente en la expresión la ligadura se denomina esclerónoma. Si el tiempo sí aparece explícitamente se llama reónoma.

Veamos algunos ejemples, con su denominación particular

Geométricas bilaterales

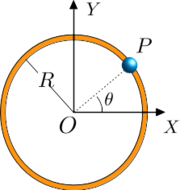
Establece una relación de igualdad entre las coordenadas. Por ejemplo, una partícula engarzada en una circunferencia de radio $R$ centrada en el origen y en el plano $O X Y$ es un ejemplo de ligadura holónoma geométrica bilateral y esclerónoma

$\begin{array}{l} z=0\\x^2+y^2=R^2. \end{array}$

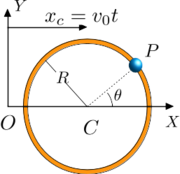
Si el aro se mueve con una velocidad prefijada, como se indica en la figura, el tiempo aparece explícitamente en la segunda ligadura, que pasa a ser reónoma.

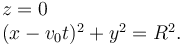
$\begin{array}{l} z=0\\(x-v_0t)^2+y^2=R^2. \end{array}$

Si una de las ligaduras es reónoma el sistema entero se denomina reónomo. En muchas ocasiones las ligaduras reónomas corresponden a vínculos con un movimiento prefijado.

Cinématicas integrables

Las ligaduras cinemáticas son aquellas en las que se imponen condiciones sobre alguna o todas las velocidades. Su forma general es

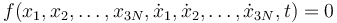
$f(x_1, x_2, \ldots, x_{3N},\dot{x}_1, \dot{x}_2, \ldots, \dot{x}_{3N},t)=0$

Si la expresión puede integrarse para eliminar las velocidades se convierte en una ligadura geómetrica bilateral. Por tanto es holónoma.

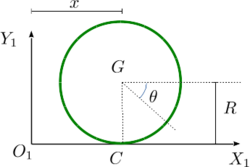
Un ejemplo muy importante en Ingeniería es la rodadura sin deslizamiento en un movimiento plano. Para el aro de radio $R$ de la izquierda tenemos

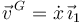
$\vec{v}^{\,G} = \dot{x}\,\vec{\imath}_1$

La condición de rodadura sin deslizamiento impone 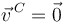$\vec{v}^{\,C}=\vec{0}$ . Usando el Teorema de Chasles

$\vec{v}^{\,G} = \vec{v}^{\,C} + \vec{\omega}\times\overrightarrow{CG} \Longrightarrow \dot{x} = R\,\dot{\theta}.$

Esta es una ligadura cinemática, pues involucra a derivadas temporales de las coordenadas generalizadas. Pero puede integrarse. La ligadura puede expresarse como

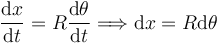
$\dfrac{\mathrm{d}x}{\mathrm{d}t} = R\dfrac{\mathrm{d}\theta}{\mathrm{d}t} \Longrightarrow \mathrm{d}x = R\mathrm{d}\theta$

Esta expresión puede integrarse

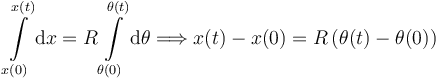
$\int\limits_{x(0)}^{x(t)}\mathrm{d}x = R\int\limits_{\theta(0)}^{\theta(t)}\mathrm{d}\theta \Longrightarrow x(t) - x(0) = R\,(\theta(t)-\theta(0))$

Obtenemos así una ligadura holónoma.

1.2 Ligaduras no holónomas

En este caso no pueden expresarse con una relación matemática de la forma $f(x_1, x_2, \ldots, x_{3N},t)=0$ . Veamos algunos ejemplos

Geométricas unilaterales

La expresión matemática del vínculo es una inegualdad que involucra a las coordenadas y, quizás, el tiempo. Por ejemplo, para una partícula botando en una mesa, de modo que el plano de la mesa es el plano $O X Y$ , la ligadura es

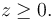
$z\geq0.$

Este ligadura es esclerónoma. Si la mesa se mueve con velocidad vertical uniforme $v 0$ la ligadura sería (suponiendo que en $t = 0$ el plano de la mesa coincide con el plano $O X Y$ )

$z\geq v_0t.$

Esta ligadura es reónoma.

Rodadura sin deslizamiento en 3D

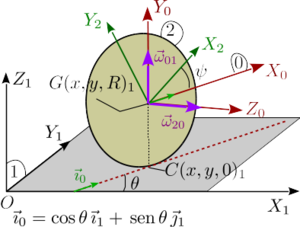
Supongamos que tenemos un disco de radio $R$ que rueda sin deslizar y pivota sobre una superficie plana, pero sin tumbarse. Podemos imaginar una moneda rodando en el suelo. Escogemos como sólido "0" un triedro cuyo origen se mueve con el centro del disco, $G$ , y el eje $G Z 0$ es siempre perpendicular al disco. El triedro "2", solidario con el disco, tiene como origen su centro y su eje $G Z 2$ coincide en todo momento con el $G Z 0$ . Las coordenadas generalizadas son las coordenadas cartesianas del centro del disco, $x, y$ , el ángulo $θ$ que forma el eje $G X 0$ con el eje fijo $O X 1$ , y el ángulo $ψ$ que forma el eje $G X 2$ con el eje $G X 0$ . Podría parecer en principio que hay 4 grados de libertad, pero sólo hay 2. Esto puede razonarse así. Un sólido rígido libre tiene 6 grados de libertad. La condición de rodadura sin deslizamiento imponte 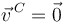$\vec{v}^{\,C}=\vec{0}$ (3 vínculos cinemáticos). Si no puede tumbarse hay una componente prohibida de la rotación. Así pues, el número de grados de libertad es $n = 6 - 4 = 2$ . Veamos como se obtienen las expresiones de las ligaduras.

Para el movimiento {01} tenemos

$\begin{array}{l} \vec{\omega}_{01} = \dot{\theta}\,\vec{k}_1,\\ \vec{v}^{\,G}_{01} = \dot{x}\,\vec{\imath}_1 + \dot{y}\,\vec{\jmath}_1,\\ \vec{v}^{\,C}_{01} = \vec{v}^{\,G}_{01} + \vec{\omega}_{01}\times\overrightarrow{GC} = \dot{x}\,\vec{\imath}_1 + \dot{y}\,\vec{\jmath}_1. \end{array}$

Para el {20}

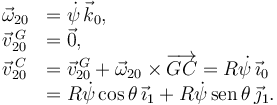
$\begin{array}{ll} \vec{\omega}_{20} & = \dot{\psi}\,\vec{k}_0,\\ \vec{v}^{\,G}_{20}& = \vec{0},\\ \vec{v}^{\,C}_{20}& = \vec{v}^{\,G}_{20} + \vec{\omega}_{20}\times\overrightarrow{GC} =R\dot{\psi}\,\vec{\imath}_0\\ & = R\dot{\psi}\cos\theta\,\vec{\imath}_1 + R\dot{\psi}\,\mathrm{sen}\,\theta\,\vec{\jmath}_1. \end{array}$

La rodadura sin deslizamiento impone 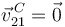$\vec{v}^{\,C}_{21}=\vec{0}$ . Entonces

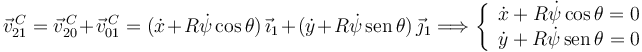
$\vec{v}^{\,C}_{21} = \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01} = (\dot{x} + R\dot{\psi}\cos\theta)\,\vec{\imath}_1 + (\dot{y} + R\dot{\psi}\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1 \Longrightarrow \left\{ \begin{array}{l} \dot{x} + R\dot{\psi}\cos\theta=0\\ \dot{y} + R\dot{\psi}\,\mathrm{sen}\,\theta=0 \end{array} \right.$

Estas ligaduras no se pueden integrar. Por ejemplo, la primera puede manipularse así

$\dfrac{\mathrm{d}x}{\mathrm{d}t} = -R\cos\theta\dfrac{\mathrm{d}\psi}{\mathrm{d}t} \Longrightarrow \int\mathrm{d}x = R\int\cos\theta\,\mathrm{d}\psi.$

La segunda integral no se puede hacer, pues $θ$ no es constante durante el movimiento y no sabemos como depende de $ψ$ . Este es un caso en el que hay que describir el sistema con cuatro coordenadas generalizadas, ${x, y,θ,ψ}$ , aunque haya sólo dos grados de libertad. Veremos mas adelante que hay técnicas para tratar este tipo de problemas.

MR 09 Ligaduras

De Laplace

1 Ligaduras

1.1 Ligaduras holónomas

1.2 Ligaduras no holónomas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES