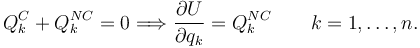MR 09 Fuerzas conservativas
De Laplace
1 Fuerzas conservativas
En un sistema conservativo todas las fuerzas aplicadas son conservativas. Por tanto, puede definirse una energía potencial del sistema. Veremos que en este caso el P.T.V. puede entenderse como búsqueda del mínimo de la energía potencial del sistema.
Tenemos la partícula de la figura sometida a ligaduras ideales y a la fuerza conservativa de la gravedad. El sistema tiene una coordenada generalizada: {θ}. Tenemos
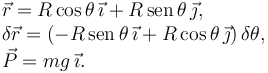
Aplicando el P.T.V. tenemos
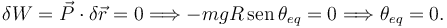
Podemos definir la energía potencial gravitatoria como
U = − mgRcosθ
En un desplazamiento virtual, la variación de energía potencial es

Es decir, para que la posición sea de equilibrio, la energía potencial no debe cambiar en un desplazamiento virtual. Esto equivale a decir que al energía potencial debe tener un extremo en el punto de equilibrio. Para que eso ocurra su derivada debe ser nula
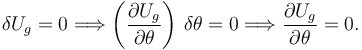
En este caso
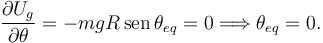
Para un sistema conservativo con n grados de libertad, una configuración del sistema es de equilibrio si la energía potencial tiene un extremo

Si el sistema es independiente, cada una de las derivadas debe anularse
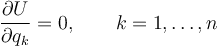
Obtenemos así n ecuaciones para las n coordenadas generalizadas {qk}.
Es interesante señalar que las fuerzas generalizadas conservativas se obtienen como derivadas de la energía potencial. Tenemos
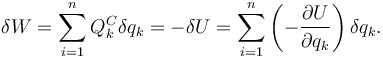
Si el sistema es independiente, para que los dos sumatorios sean iguales cada uno de los factores debe ser igual, es decir
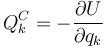
Esta es una generalización al espacio de configuraciones de la relación entre la fuerza y el gradiente de la energía potencial en Mecánica Vectorial.
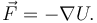
1.1 Estabilidad del equilibrio
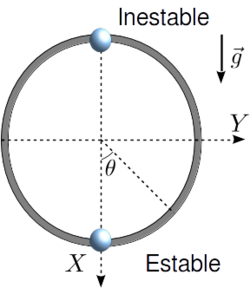
No todos los puntos de equilibrio son iguales. Supongamos una partícula engarzada en un aro vertical liso sometida a la acción de la gravedad. La condición de equilibrio sobre la energía potencial nos da dos posiciones de equilibrio

Las posiciones de equilibrio son
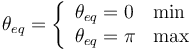
El mínimo corresponde a un equilibrio estable. Si la posición de la partícula es perturbada ligeramente las fuerzas que actúan hacen que vuelva a la posición de equilibrio. En el caso del máximo el equilibrio es inestable. Tras una pequeña perturbación la partícula se aleja cada vez más de la posición de equilibrio.
Si el sistema tiene sólo un grado de libertad la derivada segunda del pontencial en los puntos de equilibrio nos da el carácter del equilibrio

El último caso aparece cuando el potencial es plano en el punto de equilibrio. Un ejemplo sería un bloque apoyado en una mesa horizontal sin rozamiento. Todos los puntos de la mesa son de equilibrio.
Cuando el sistema tiene varios grados de libertad la posición de equilibrio debe ser un mínimo local para que sea de equilibrio estable. En la figura la posición de la izquierda es de equilibrio estable, mientras que la de la derecha es inestable.
1.2 Aplicación a sistemas no conservativos
La formulación del P.T.V. en términos de la energía potencial no es aplicable si hay fuerzas no conservativas en el sistema, como el rozamiento. En ese caso, puede considerarse que las fuerzas generalizadas tienen dos contribuciones: una que proviene de las fuerzas conservativas y otra de las no conservativas.

El P.T.V. puede expresarse como
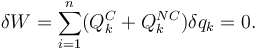
Si el sistema es independiente la condición de equilibrio es