Introducción al electromagnetismo (GIOI)

De Laplace

Contenido

1 Las cuatro fuerzas de la naturaleza
2 Interacción electromagnética
3 Carga eléctrica
4 Leyes del electromagnetismo
- 4.1 Ley de Lorentz
- 4.2 Ecuaciones de Maxwell
5 Campos
- 5.1 Líneas de campo
6 División del electromagnetismo

1 Las cuatro fuerzas de la naturaleza

En una descripción fundamental de los procesos físicos, estos pueden considerarse como manifestaciones de cuatro interacciones:

Gravedad
Electromagnetismo
Interacción nuclear fuerte
Interacción nuclear débil

En este modelo (el llamado “modelo estándar”) lo que vemos como diferentes fuerzas macroscópicas (elásticas, de rozamiento, impulsos en las colisiones, etc.) son en realidad manifestaciones de estas interacciones fundamentales. Las principales propiedades de cada una son:

De xkcd

Gravedad: Es una interacción entre masas. Su principal efecto a escala humana es el peso y a grandes escalas es la responsable del movimiento planetario y estelar. Es una fuerza de largo alcance (teóricamente infinito).

Electromagnetismo: Es la interacción entre cargas eléctricas, que se manifiesta por medio de campos eléctricos y de campos magnéticos, relacionados entre sí. Es una fuerza de largo alcance (teóricamente infinito), mucho más intensa que la gravedad.

Fuerza nuclear fuerte: Es una interacción entre partículas elementales (quarks) caracterizadas por un tipo de carga llamado “color”. Los quarks se asocian formando protones y neutrones.

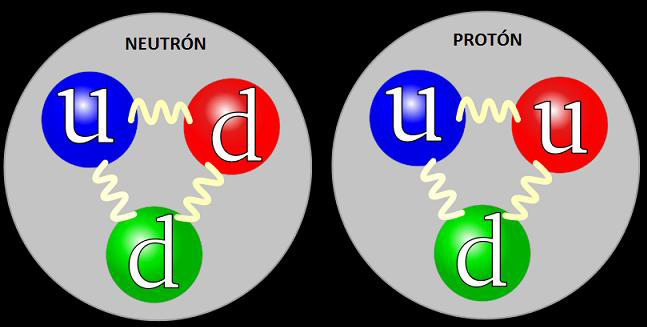
La fuerza nuclear fuerte es responsable de la cohesión de los núcleos, ya que es capaz de vencer la repulsión eléctrica entre los protones. Es una fuerza de muy corto alcance; a distancias mayores de

10 - 13

es inapreciable.

{

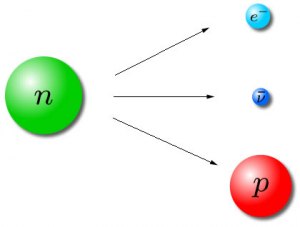
Fuerza nuclear débil: Es responsable de algunos procesos nucleares, como la desintegración beta del neutrón, que espontáneamente se descompone en un protón, un electrón y un antineutrino. Es también de muy corto alcance y mucho menos intensa que el electromagnetismo y la fuerza nuclear fuerte.

De estas cuatro fuerzas, las dos nucleares tienen efectos solo indirectos a escala macroscópica. La gravedad es muy débil y solo es apreciable si la acumulación de masa es muy grande (por ejemplo, el peso es una fuerza apreciable porque la Tierra tiene una masa de unos 6×10²⁴kg).

Esto quiere decir que todas las fuerzas que apreciamos a nuestro alrededor, excluyendo el peso, son fuerzas electromagnéticas. Una fuerza de contacto, como la que produce un cuerpo que empuja a otro, es realmente una fuerza de repulsión entre las nubes electrónicas de los átomos de un cuerpo con las de los del otro.

2 Interacción electromagnética

El electromagnetismo corresponde a la interacción entre cargas eléctricas. Se describe en términos de cargas que interaccionan por medio de campos eléctricos y magnéticos. La teoría electromagnética nace de la síntesis efectuada por Maxwell de las teorías existentes sobre las fuerzas eléctricas y las fuerzas magnéticas, hasta entonces tratadas como fuerzas separadas aunque relacionadas.

En el electromagnetismo hay fuentes, que son las partículas que producen los campos. Estas fuentes son las cargas eléctricas y las corrientes eléctricas (más los dipolos magnéticos, responsables del magnetismo de algunos materiales, como el hierro). Estas fuentes producen dos campos, el campo eléctrico y el magnético, que a su vez pueden considerarse como dos aspectos del mismo campo electromagnético. Los dos campos actúan sobre las cargas y corrientes produciendo fuerzas sobre ellas y causando su movimiento (que a su vez modifica los campos eléctrico y magnético).

Así mismo, un campo eléctrico variable en el tiempo genera un campo magnético y viceversa, aunque no haya cargas ni corrientes presentes. Esta es la base de las ondas electromagnéticas, que se propagan por el espacio vacío.

3 Carga eléctrica

La carga eléctrica es una propiedad fundamental de la materia. Una determinada partícula posee carga o es neutra, pero no se puede describir qué es la carga eléctrica. El electromagnetismo es una interacción entre partículas cargadas y una partícula posee carga cuando interacciona electromagnéticamente.

Aunque no se pueda decir qué es la carga, si se pueden caracterizar sus propiedades principales.

3.1 Propiedad escalar

La carga de un sistema es una propiedad escalar, caracterizada por una magnitud y un signo, pero no tiene dirección ni sentido.

Se mide en el SI en un culombio (C) definido como

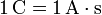
$1\,\mathrm{C}=1\,\mathrm{A}\cdot\mathrm{s}$

(con la A de amperio, que se ve al estudiar la corriente eléctrica). Un culombio es una cantidad gigantesca, imposible de reunir en la práctica debido a la repulsión entre cargas del mismo signo. Por ello, es mucho más frecuente usar unidades como nanoculombios o picoculombios.

3.2 Dos tipos de carga

Existen dos variedades de carga eléctrica. A diferencia de la masa, que es solo de un tipo, o del color de los quarks (que es de tres variedades), la carga eléctrica se presenta en dos tipos diferentes, denominados por convenio carga positiva (que representamos con el signo + y el color rojo) y carga negativa (representada por el signo − y el color azul). La carga positiva es la que es del mismo tipo que la del protón y la negativa la que es del mismo tipo que la del electrón.

El que haya solo dos tipos de carga permite sumarlas como números ordinarios, de manera que si se unen dos partículas de cargas $q 1$ y $q 2$ , la carga del conjunto es $q 1 + q 2$ (esto también se puede hacer con la masa, pero no con el color de los quarks ¿cuánto es la suma de unir una partícula “roja” con una “verde”?).

3.3 Ley de conservación de la carga

La carga se conserva. Esta es una de las propiedades básicas de la interacción electromagnética. A diferencia de otras magnitudes, como la energía mecánica o la entropía, la carga se conserva en cualquier sistema. Esto quiere decir que

En cualquier punto del espacio, la carga no se crea ni se destruye.

o, expresado de forma más precisa, cuya formulación matemática veremos más adelante:

Para cualquier volumen, el cambio de la carga contenida en su interior se produce siempre por una entrada o salida a través de la frontera, nunca por producción o destrucción en el volumen.

Hay que precisar qué significa que no se puede producir carga, ya que, como hemos comentado antes, puede ocurrir que un neutrón -que no tiene carga- se desintegre, produciendo un protón, que es una partícula cargada. Lo que ocurre es que al mismo tiempo se genera un electrón, que es una partícula con una carga opuesta a la del protón, de manera que la carga total permanece constante.

3.4 Cuantización de la carga. Densidad de carga

En los primeros tiempos de la teoría electromagnética se consideraba que la electricidad era un fluido (aun se habla de “corte de fluido eléctrico”), que se podía dar en cualquier cantidad. Sin embargo, los experimentos de Thomson, descubridor del electrón en 1897, mostraron que la carga presente en cualquier sistema es siempre un múltiplo entero de una carga fundamental

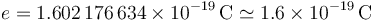
$e = 1.602\,176\,634\times 10^{-19}\,\mathrm{C}\simeq 1.6\times 10^{-19}\,\mathrm{C}$

Las partículas elementales tienen siempre una carga que es un múltiplo entero de esta: un protón tiene una carga $+ e$ y un electrón una carga $- e$ , los neutrones, neutrinos y fotones tienen carga 0. Los átomos y moléculas, compuestos de estas partículas, tienen una carga que será

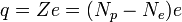
$q = Ze = (N_p-N_e)e\,$

siendo $N p$ y $N e$ el número de protones y electrones, respectivamente. Esto se extiende a cualquier trozo de materia, que tendrá por tanto una carga que será un múltiplo entero de la carga elemental.

Ahora bien, para cualquier cantidad finita de materia, el número de cargas contenidas es gigantesco. Tomemos un elemento de volumen microscópico de agua, de 1 μm³ de volumen. La cantidad de moléculas contenidas en él es

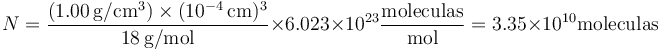
$N = \frac{(1.00\,\mathrm{g}/\mathrm{cm}^3)\times (10^{-4}\,\mathrm{cm})^3}{18\,\mathrm{g}/\mathrm{mol}}\times 6.023\times 10^{23}\frac{\mathrm{moleculas}}{\mathrm{mol}}=3.35\times 10^{10}\mbox{moleculas}$

Cada molécula contiene 10 protones y 10 electrones, lo que nos da 0.67 billones de cargas elementales, la mitad de cada signo.

El que el número de cargas en cualquier medio material sea tan gigantesco tiene tres consecuencias prácticas importantes:

Si a esta cantidad le sumamos o restamos unos cuantos electrones, el efecto puede tratarse como un diferencial de carga. Por ello, para el electromagnetismo macroscópico, la carga puede tratarse como un continuo, y se pueden hacer integrales y derivadas como con cualquier otra cantidad.
Al decir que un volumen es neutro o que está descargado, no estamos diciendo que no haya cargas en él, sino que hay tantas cargas positivas como negativas (y puede haber billones de cada tipo). De un volumen material descargado siempre vamos a poder extraer carga porque hay millones disponibles.
El manejo de un número tan grande de cargas impide tratarlas individualmente mediante sumatorios. Se hace preciso trabajar con densidades de carga.

3.4.1 Densidades de carga

De volumen, ρ: Si dividimos un volumen en elementos microscópicos (de 1μm³, por ejemplo), definimos la densidad volumétrica de carga como la suma de todas las cargas que hay dentro dividida por el volumen del elemento

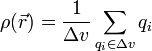
$\rho(\vec{r})=\frac{1}{\Delta v}\sum_{q_i\in\Delta v}q_i$

siendo $\vec{r}$ la posición del elemento de volumen. Esta densidad se mide en C/m³. Conocida la densidad de carga, el diferencial de carga contenida en un elemento y la carga total de todo el volumen valen

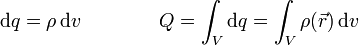
$\mathrm{d}q=\rho\,\mathrm{d}v\qquad\qquad Q = \int_V \mathrm{d}q=\int_V\rho(\vec{r})\,\mathrm{d}v$

De superficie, $σ s$ : En ocasiones toda la carga neta de un sistema está concentrada en una capa muy fina. En ese caso se define la densidad de carga superficial (medida en C/m²) como

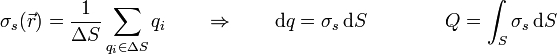
$\sigma_s(\vec{r})=\frac{1}{\Delta S}\sum_{q_i\in\Delta S}q_i\qquad\Rightarrow\qquad \mathrm{d}q=\sigma_s\,\mathrm{d}S\qquad\qquad Q = \int_S\sigma_s\,\mathrm{d}S$

Lineal, $λ$ : En sistemas como un hilo la carga se distribuye a lo largo de una línea (curva en general). En ese caso se define la densidad lineal de carga (medida en C/m) como

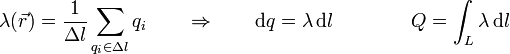
$\lambda(\vec{r})=\frac{1}{\Delta l}\sum_{q_i\in\Delta l}q_i\qquad\Rightarrow\qquad \mathrm{d}q=\lambda\,\mathrm{d}l\qquad\qquad Q = \int_L\lambda\,\mathrm{d}l$

En general podemos tener una combinación de todos los tipos de densidades, por lo que la carga total será la suma de todas ellas

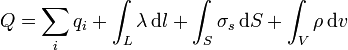
$Q = \sum_i q_i + \int_L\lambda\,\mathrm{d}l + \int_S\sigma_s\,\mathrm{d}S + \int_V\rho\,\mathrm{d}v$

3.4.2 Densidades uniformes

En muchos problemas prácticos se dice “una carga Q distribuida uniformemente en el volumen” o “un anillo cargado uniformemente con carga Q” o similar. En estos casos se nos está dando el tipo de distribución (si es de volumen, lineal, etc.), el valor de la carga total, y se nos dice que la carga tiene una densidad uniforme, es decir, que es la misma para todos los puntos. En esos casos, lo primero es determinar la densidad correspondiente, y luego recurrir a las expresiones para el cálculo de campos y potenciales eléctricos.

Si nos dicen que tenemos una carga Q distribuida uniformemente, su densidad será

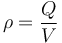
$\rho=\frac{Q}{V}$

que para el caso de una esfera maciza se reduce a

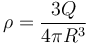
$\rho=\frac{3Q}{4\pi R^3}$

Análogamente si tenemos el caso de una carga distribuida uniformemente en una superficie esférica

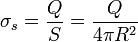
$\sigma_s = \frac{Q}{S}=\frac{Q}{4\pi R^2}$

Y si es en un anillo

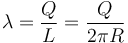
$\lambda= \frac{Q}{L}=\frac{Q}{2\pi R}$

4 Leyes del electromagnetismo

A modo de introducción y resumen, vamos a enunciar las leyes que gobiernan la interacción electromagnética clásica. Estas leyes fueron formuladas por Maxwell en 1861-1862 y en combinación con la ley de Lorentz para la fuerza sobre una carga eléctrica permiten describir todos los fenómenos electromagnéticos, por diferentes que sean.

4.1 Ley de Lorentz

La expresión que da la fuerza sobre una carga puntual $q$ que se mueve en un campo electromagnético lo da la Ley de Lorentz:

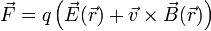
$\vec{F}=q\left(\vec{E}(\vec{r})+\vec{v}\times\vec{B}(\vec{r})\right)$

siendo $\vec{r}$ la posición instantánea que la carga y $\vec{v}$ su velocidad. Vemos que los campos eléctrico y magnético actúan de diferente manera sobre una carga, requiriendo la fuerza magnética que la carga esté en movimiento.

De la expresión de la ley de Lorentz, obtenemos las unidades de medida de los dos campos:

El campo eléctrico se mide en N/C (aunque es más frecuente medirlo en V/m, que es la misma unidad)
El campo magnético se mide en N/(C·m/s) = N/(A·m). A esta unidad se la denomina tesla (T)

En esta expresión, los campos son los producidos por el resto de cargas del universo, ya que una carga no produce fuerza sobre sí misma.

Nótese que en la ley de Lorentz no precisamos saber quién produce los campos, si una carga, un conjunto de ellas, o una distribución continua, o si están en movimiento o en reposo. Lo único que necesitamos es el valor del campo en la posición de la carga. Por ello, la introducción de los campos transforma un problema de fuerzas a distancias entre cargas, en uno local, donde cada carga solo percibe lo que le rodea.

Si conocemos las distribuciones de campos, el problema mecánico para el movimiento de la carga consiste en la resolución de las leyes de Newton

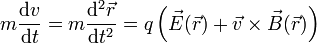
$m\frac{\mathrm{d}v}{\mathrm{d}t} = m\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2} = q\left(\vec{E}(\vec{r})+\vec{v}\times\vec{B}(\vec{r})\right)$

La solución de este problema dinámico puede ser extremadamente complicada incluso para casos de campos simples. Entre los que tienen solución analítica están:

El movimiento de una carga en un campo eléctrico uniforme, sin campo magnético: Este problema es equivalente al de una partícula sometida a la acción del peso, y el resultado es un movimiento parabólico
El caso de una carga puntual en el campo eléctrico de otra carga puntual en reposo: En este caso el campo magnético es nulo y el problema es equivalente al del movimiento planetario. El resultado es que la carga describe una cónica (circunferencia, elipse, parábola o hipérbola).
El caso de una carga en un campo magnético uniforme, sin campo eléctrico: tal como se ve en un problema el resultado es un movimiento helicoidal (que puede ser rectilíneo o circular en casos particulares).

4.2 Ecuaciones de Maxwell

La ley de Lorentz nos da la fuerza sobre una carga conocidos los campos eléctrico y magnético. Las ecuaciones de Maxwell nos describen cómo son estos campos en función de las cargas que los producen y cómo se relacionan entre sí. Las ecuaciones de Maxwell son cuatro, cada una con un nombre propio

4.2.1 Ley de Gauss

El flujo del campo eléctrico a través de una superficie cerrada es igual a la carga encerrada por la superficie, dividida por una constante universal, denominada permitividad del vacío

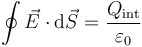
$\oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}$

4.2.2 Ley de Faraday

La circulación del campo eléctrico a lo largo de una curva cerrada es igual a la derivada temporal, cambiada de signo, del flujo magnético a través de una superifice apoyada en dicha curva y orientada según la regla de la mano derecha

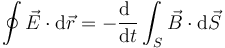
$\oint \vec{E}\cdot\mathrm{d}\vec{r}=-\frac{\mathrm{d}\ }{\mathrm{d}t}\int_S\vec{B}\cdot\mathrm{d}\vec{S}$

4.2.3 Ley de Gauss para el campo magnético

El flujo del campo magnético a través de toda superficie cerrada es nulo

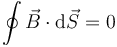
$\oint \vec{B}\cdot\mathrm{d}\vec{S}=0$

4.2.4 Ley de Ampère-Maxwell

La circulación del campo magnético a lo largo de una curva cerrada es proporcional a la suma de dos términos: uno igual a la corriente eléctrica que atraviesa una superficie apoyada en una curva y otro proporcional a la derivada temporal del flujo eléctrico

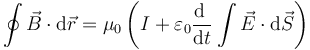
$\oint \vec{B}\cdot\mathrm{d}\vec{r} = \mu_0\left( I + \varepsilon_0\frac{\mathrm{d}\ }{\mathrm{d}t}\int \vec{E}\cdot\mathrm{d}\vec{S}\right)$

5 Campos

La interacción entre las cargas eléctricas puede expresarse mediante fuerzas de acción a distancia, tal como hizo Newton con la ley de la Gravitación Universal. En esta formulación la Tierra atrae a la Luna simplemente porque está ahí, sin importar qué haya entre los dos cuerpos. La ley de Coulomb para la fuerzas entre cargas sigue la misma filosofía.

Sin embargo, es mucho más productivo el concepto, inventado por Faraday, de campo eléctrico, campo magnético (y campo electromagnético, fusión de los dos). Por medio del campo, la interacción entre dos cargas se separa en dos partes:

Por un lado, la simple existencia de una carga provoca una perturbación en el espacio, que denominamos su campo electromagnético. Esta perturbación se extiende a todo el espacio, no solamente en la posición de la carga, aunque lógicamente es más intensa cuanto más nos acercamos a ella.
Al situar una segunda carga, esta lo que percibe no es a la primera, sino al campo que crea, es decir, el campo actúa como intermediario para la interacción entre las cargas.

La analogía mecánica más sencilla es con un resorte (esta analogía es muy adecuada, pues el campo eléctrico se comporta en muchos aspectos como una fuerza elástica, y usaremos la analogía reiteradamente). Si tenemos dos masas sujetas en los extremos de un resorte, al tirar de una de ellas, podremos pensar que la otra ejerce sobre ésta una fuerza dada por la ley de Hooke 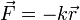$\vec{F}=-k\vec{r}$ . Sin embargo, es más simple pensar que la fuerza la ejerce el propio muelle y que lo que nota la segunda masa no es la presencia de la primera masa, sino el muelle al que esta sujeta. Con el campo electromagnético es exactamente lo mismo, solo que ahora el muelle es invisible (pero, como sabe cualquiera que haya acercado dos imanes por sus polos del mismo signo, es claramente perceptible).

El estudio del electromagnetismo, por tanto, se separa en dos problemas relacionados:

El estudio de los campos eléctricos y magnéticos creados por cargas en reposo o en movimiento.
El estudio del efecto que esos campos tienen sobre otras cargas.

La segunda parte contiene en gran medida elementos de dinámica, pues se trata de analizar la evolución de un sistema sabiendo las fuerzas que actúan sobre él.

Aquí nos centraremos sobre todo en la primera parte, determinando campos eléctricos y magnéticos en diferentes sistemas.

Una carga eléctrica produce un campo electromagnético, que se manifiesta de dos campos diferentes:

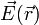El campo eléctrico, $\vec{E}(\vec{r})$ .
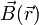
El campo magnético, $\vec{B}(\vec{r})$

El eléctrico se produce en cualquier circunstancia, mientras que el magnético sólo cuando la carga se encuentra en movimiento. Estos campos interactúan entre sí y a través del fenómeno de la inducción, un campo eléctrico produce uno magnético y viceversa.

Matemáticamente, un campo vectorial es una función matemática que a cada punto del espacio le hace corresponder un vector, que es el valor del campo en dicho punto

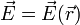
$\vec{E}=\vec{E}(\vec{r})$

Esto convierte a un campo vectorial en un vector ligado, asociado a cada punto. No tenemos permiso, por tanto, para desplazarlo de un punto a otro o sumar los campos de diferentes puntos.

5.1 Líneas de campo

Una de las herramientas más útiles para visualizar los campos vectoriales consisten en trazar sus líneas de campo. Una línea de campo es una curva que en todo punto es tangente a la dirección del campo en dicho punto.

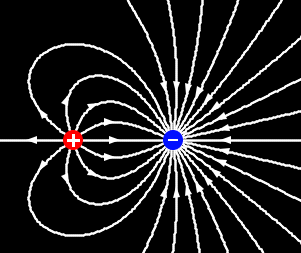
Mátemáticamente la ecuación de una línea de campo se halla partiendo de un punto del espacio. En ese punto el campo eléctrico apunta en una dirección determinada. Se realiza un desplazamiento en dicha dirección, llegando a un punto próximo, en el cual el campo apuntará en una dirección ligeramente diferente, se continúa en esa dirección y así sucesivamente. Para cada paso se cumple

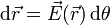
$\mathrm{d}\vec{r}=\vec{E}(\vec{r})\,\mathrm{d}\theta$

siendo $θ$ un parámetro que nos da los diferentes puntos de la curva.

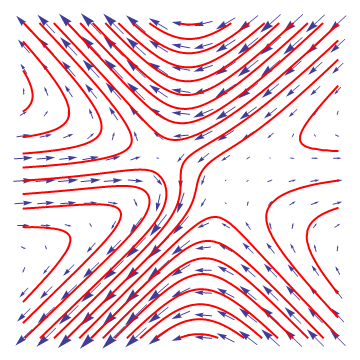
Dado que los campos poseen un único valor en cada punto, por cada punto del espacio pasa una y solo una línea de campo, que por tanto no se cortan entre sí.

Las líneas de campo constituyen una visualización de los campos eléctricos y magnéticos, pero nada más:

Al hablar de los campos, se suele decir, por ligereza del lenguaje, "y el campo se desvía hacia este lado", etc. El campo no se desvía hacia ningún sitio, ni se mueve de donde está. Lo que significa esta frase es que la línea de campo tangente al campo se curva en la dirección indicada.
Las líneas no representan la dirección de movimiento de nada. Una carga que se libere en un campo eléctrico o magnético describirá en general un movimiento complicado que puede ser ortogonal a las líneas de campo.

6 División del electromagnetismo

La teoría electromagnética es un cuerpo único descrito por un solo conjunto de leyes, conocidas como ecuaciones de Maxwell. Sin embargo, dada la enorme variedad de sistemas posibles, conviene hacer una división en dominios más reducidos, atendiendo esencialmente a la dependencia de los campos con el tiempo.

Electrostática

Consiste en el estudio de los campos y fuerzas producidos por cargas en reposo, en ausencia de campos magnéticos. A su vez, la electrostática se divide en dos partes principales:

Electrostática en el vacío: describe los campos y fuerzas de cargas consideradas como entes que flotan en el vacío. Puesto que la materia es un 99% vacío, es útil como punto de partida.
Electrostática en medios materiales: Apoyándose en lo anterior, estudia los campos y fuerzas cuando en el sistema existen materiales conductores y dieléctricos. Aunque en un medio conductor las cargas pueden moverse, se consideran solo los casos en que están en reposo (equilibrio electrostático).

Corriente eléctrica

Estudia el efecto del movimiento de cargas por el interior de los materiales. A su vez, se divide en dos casos:

Corriente continua o estacionaria: es aquella que no depende del tiempo. Es un caso no electrostático (pues las cargas se mueven), pero que produce campos independientes del tiempo.

Magnetostática: Estudia los campos magnéticos independientes del tiempo, que son producidos por corrientes continuas o por dipolos magnéticos (imanes). Como la electrostática, se divide en su estudio en el vacío y en medios materiales.
Electromagnetismo: Considera el caso general de campos eléctricos y magnéticos variables en el tiempo. En este caso, no se pueden considerar por separado, ya que los campos eléctricos inducen campos magnéticos y viceversa.
Óptica: Uno de los descubrimientos de Maxwell al establecer sus ecuaciones fue el incluir la luz como una forma de radiación electromagnética. Por ello, todas las leyes de la óptica pueden deducirse también de la teoría electromagnética, aunque suelen estudiarse por separado.