Intensidad en función de la temperatura Primera Prueba de Control 2010/11 (F2GIA)
De Laplace
1 Enunciado
En el desierto del Sahara, con una temperatura de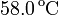 
se aplica a un cable de cobre una diferencia de potencial ΔV0. Por el cable circula una corriente de 
. Se lleva ese mismo cable a la Antártida, con una temperatura de 
. Si se aplica al cable la misma diferencia de potencial ΔV0 de la misma manera que en el Sahara, ¿que corriente se mide ahora?
Datos: resistividad del cobre a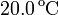 
: 
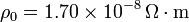, coeficiente de temperatura del cobre a : 
.
-
.
-
.
-
.
-
.
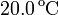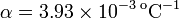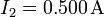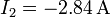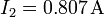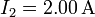2 Solución
La respuesta correcta es la 4.
La resistividad de un material depende con la temperatura. En clase hemos expresado esta variación con la ley
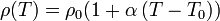
siendo T0 una temperatura de referencia, ρ0 la resistividad a esa temperatura y α el coeficiente de temperatura del material también a esa temperatura.
Para un hilo, la resistencia es
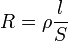
Al variar la temperatura, la longitud y la sección del hilo también cambian. Sin embargo, esta variación es despreciable frente a la debida a la dependencia de la resistividad con la temperatura. Entonces podemos escribir para la resistencia de un hilo
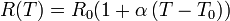
siendo R0 la resistencia del hilo a la temperatura de referencia.
El enunciado nos dice que la corriente medida a la temperatura 
es de para una tensión V0. Usando la expresión anterior tenemos que la resistencia a esta temperatura es
R1 = R0(1 + α(T1 − T0))
T0 son 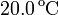y R0 es la resistencia a 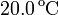, que no conocemos.
En la Antártida el hilo está a una temperatura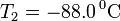 
. Su resistencia ahora es
R2 = R0(1 + α(T2 − T0))
Dividiendo las dos resistencias tenemos
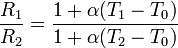
Si aplicamos el mismo potencial al hilo tenemos
Tiene sentido que la intensidad sea mayor en la Antártida, pues la resistencia del cobre disminuye con la temperatura. Si el potencial aplicado es el mismo, la intensidad debe ser mayor.
