Generadores (GIOI)

De Laplace

Contenido 1 Definición 2 Fuerza electromotriz y resistencia interna 2.1 Valor en circuito abierto 2.2 Valor en circuito cerrado 3 Ley de Ohm generalizada 4 Ley de Kirchhoff para las mallas 5 Potencia de un generador

1 Definición

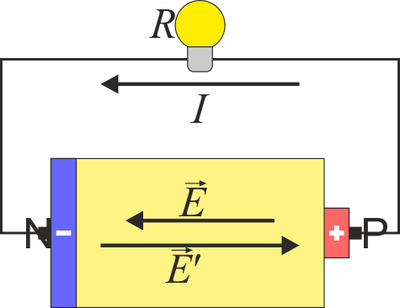
Es fácil demostrar que en un circuito cerrado no es posible que se cumple la ley de Ohm en todos sus puntos. Supongamos dos puntos del circuito P y N tales que V_P > V_N y que estos puntos están conectados por un cable de resistencia R en este caso habrá una corriente fluyendo de P a N y en el cable la densidad de corriente y el campo eléctrico irán en el mismo sentido. Pero, ¿qué ocurre al cerrar el circuito? Para obtener una corriente continua la intensidad de corriente debe ir de N a P por el resto del circuito, pero el campo eléctrico, que va de mayor a menor potencial, va de P a N. Por tanto, debe haber una porción de circuito en la cual la densidad de corriente vaya en sentido contrario al campo eléctrico. La parte del circuito en que esto ocurre se denomina el generador (o fuente).

Un circuito en el que la corriente viajara siempre “cuesta abajo” es tan imposible como las escaleras del grabado de Escher (en realidad, algo menos imposible). Las cargas positivas y las negativas harían el papel de los caminantes en la escalera

Un generador es entonces un elemento de circuito en el que la densidad de corriente va en sentido opuesto al campo eléctrico (no cumpliéndose por tanto la ley de Ohm) o en términos de circuitos, que la corriente va de menor a mayor potencial. Un generador, por tanto, viene a ser equivalente a una bomba que eleva el agua hasta una cierta altura, venciendo la fuerza de la gravedad.

Para hacerlo debe haber una fuerza actuando sobre las cargas, además de la fuerza eléctrica

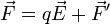
Esta fuerza adicional no puede ser debida a un campo electrostático. Entre los distintos tipos de generadores tenemos fuerzas:

• Mecánicas, en la que la carga es arrastrada contra el campo eléctrico.
• Químicas, como en las pilas o baterías, donde una reacción química separa las cargas positivas de las negativas.
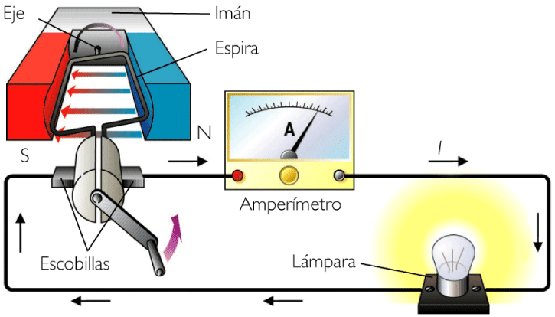
• Magnéticas, como en los generadores industriales, alternadores o dinamos.
• Eléctricas no electrostáticas. En el fenómeno de la inducción electromagnética, un campo magnético variable es capaz de producir un campo eléctrico lo que también se aplica en alternadores y dinamos.

                 

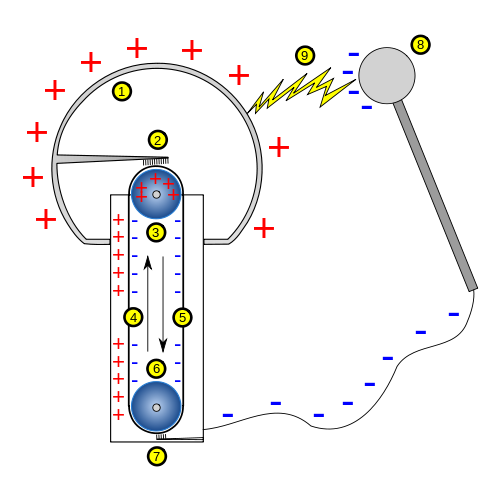
El modelo más sencillo de generador mecánico es el Van de Graaff, encontrándose el más grande del mundo en el Museo de la Ciencia de Boston. Un generador Van de Graaff se basa en primer lugar en separación de carga por fricción (o de otras formas) y su arrastre por una cinta aislante. Mediante un par de electrodos se consigue acumular carga positiva en un sitio (la corona exterior en el esquema) y negativa en otro (la tierra y el electrodo a tierra). En el propio generador el campo va de las cargas positivas a las negativas (hacia abajo en el esquema) pero la corriente va en sentido contrario (en el esquema descienden cargas negativas, lo que supone una corriente hacia arriba).

El circuito se cierra colocando algún cable o simplemente por descargas a través del aire. En el exterior la corriente va de las cargas positivas a las negativas, como es de esperar.

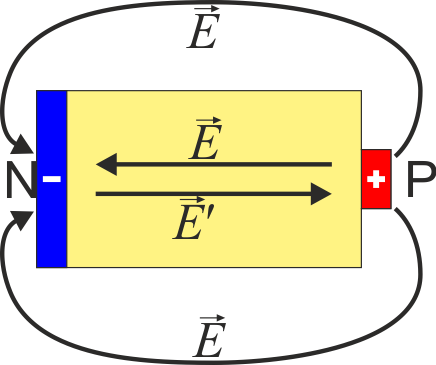
Todos los generadores se caracterizan por tener un polo positivo o ánodo (P) y un polo negativo o cátodo (N), en los que se acumulan las cargas de cada signo. La separación de cargas produce un campo eléctrico que tiende a reunirlas. La separación es conseguida por las fuerzas no electrostáticas que igualan o superan a las eléctricas.

La fuerza por unidad de carga puede escribirse en la forma

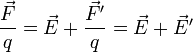
donde 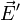no es un verdadero campo eléctrico, sino un campo efectivo, que mide la fuerza adicional que actúa sobre las cargas. Este campo efectivo solo existe dentro de los generadores.

2 Fuerza electromotriz y resistencia interna

Para medir cómo de potente es un generador se define la fuerza electromotriz (f.e.m.) 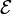. Para ello se considera una curva cerrada que va del polo positivo al negativo del generador por su exterior y de N a P por el interior. La fuerza electromotriz es igual al trabajo por unidad de carga para recorrer esta curva cerrada

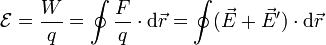
De la definición se ve que la f.e.m. no es una fuerza en absoluto, ya que se mide en voltios (V).

2.1 Valor en circuito abierto

Un circuito está abierto cuando hay una interrupción en él que impide que circule la corriente (por ejemplo, una pila no conectada a nada estaría en circuito abierto). La fuerza electromotriz se puede descomponer en suma de dos integrales

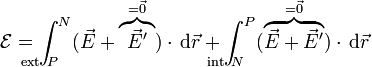
En el tramo exterior el campo efectivo es nulo porque éste solo existe dentro de los generadores. En el interior, puesto que no hay corriente y las cargas están en reposo, la fuerza sobre cada una se anula

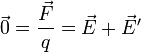
por lo que la fuerza electromotriz se reduce a

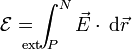
pero esta integral no es otra que la diferencia de potencial

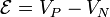
Por tanto, la diferencia de potencial entre los polos coincide con la fuerza electromotriz en circuito abierto. Esto nos proporciona un método sencillo de medir la f.e.m de una fuente: basta colocar un voltímetro entre sus polos cuando no está conectada a nada.

2.2 Valor en circuito cerrado

Cuando la fuente está conectada a un circuito ya habrá en general una corriente circulando por su interior. Al salir la corriente del polo positivo y llegar al negativo se está produciendo una descarga parcial de los polos. Aunque el campo efectivo sigue separando las cargas por dentro del generador, parte de ellas vuelven por fuera. Al reducirse la cantidad de carga en los polos, el campo eléctrico se reduce y ya dentro del generador

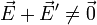
la reducción del campo eléctrico depende de cuanta carga se está escapando de los polos en cada momento, es decir de cuánta corriente está circulando. En primera aproximación, será proporcional a la corriente y podemos escribir

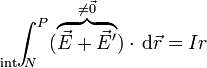
siendo r una constante de proporcionalidad que depende de la naturaleza del generador. A esta constante se la denomina resistencia interna. Con este cambio, la f.e.m. equivale a

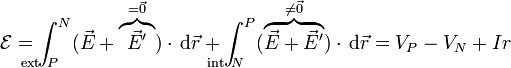
y despejando

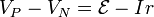
En un circuito cerrado la diferencia de potencial entre los polos es menor que la f.e.m. de la fuente. La diferencia la da el término Ir que podemos leer como la d.d.p. en una resistencia r.

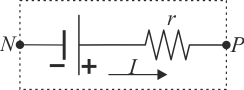
El circuito equivalente a una fuente de tensión real está formado por dos elementos: una fuente ideal (sin resistencia interna), que se indica con dos líneas desiguales, siendo la más corta el polo negativo, puesta en serie con una resistencia r.

3 Ley de Ohm generalizada

Supongamos que tenemos un circuito sencillo formado por un generador real al que se conecta una resistencia R (como podría ser una bombilla). En este caso, tenemos por un lado que

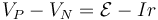
y por otro que es esta d.d.p. la que alimenta la bombilla

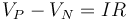
Igualando y despejando nos queda

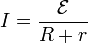
que constituye la ley de Ohm generalizada: la corriente en un circuito simple es igual a la f.e.m. dividida por la suma de todas las resistencias, tanto externas como internas.

En este caso la tensión a la salida de la fuente es

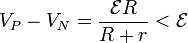
4 Ley de Kirchhoff para las mallas

La ecuación anterior se generaliza un circuito general. Una malla es un circuito cerrado, aunque puede tener derivaciones, de forma que la intensidad de corriente no tiene el mismo valor en todos los puntos. Además puede haber varios generadores en la malla. En ese caso, cuando recorremos la malla se verifica

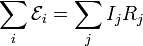
donde las R_j son todas las resistencias (tanto internas como externas) e I_j es la corriente que va por cada una. Las fuerzas electromotrices son positivas si se recorren del polo negativo al positivo, y negativas si se recorren en sentido contrario.

Esta es la ley de Kirchhoff para las mallas (o segunda ley de Kirchhoff).

        

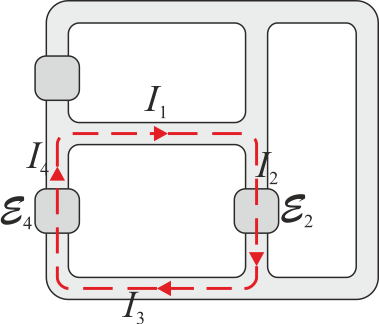
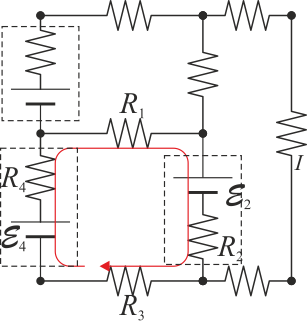
En el circuito de la figura tendríamos, para la malla señalada

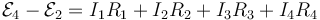
y relaciones análogas para las otras dos mallas.

En muchos casos, en lugar de trabajar directamente con esta ley es preferible emplear los voltajes de los distintos nodos y razonar a partir de ellos.

5 Potencia de un generador

Un generador tiene también un aspecto energético. En un circuito cerrado, se disipa energía en las resistencias, en las que se produce calor. Si no hay aporte externo al sistema, esa energía disipada debe proceder de otra parte del circuito. Esa otra parte son los generadores, que no solo producen la corriente, sino que aportan la potencia eléctrica asociada a ellas.

Sabemos que en un sistema con varios puntos de entrada y salida de corriente, el flujo de trabajo (potencia) se puede calcular como

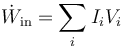
En el caso de un generador se aplica la misma ley. Por tanto

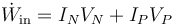
Ahora bien, dentro de un generador, la corriente va del polo negativo al positivo, por lo que

lo que da

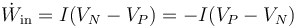
Puesto que el polo positivo se encuentra a un mayor voltaje que el negativo, vemos que este flujo de trabajo es negativo, es decir, que realmente está saliendo energía eléctrica del generador (como debe ser). Podemos ponerlo con signo positivo considerando un flujo de trabajo hacia afuera

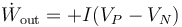
Si sustituimos aquí la diferencia de potencial entre bornes queda

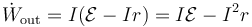
que podemos leer como que la energía que escapa del generador es la que daría un generador ideal (sin resistencia interna) menos la que se consume en el propio generador (por la presencia de r).

Si consideramos un circuito simple, formado por un generador real y una resistencia externa R, entonces podemos dividir el circuito en dos sistemas. En la resistencia

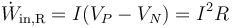
y en el generador

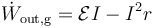
Puesto que no hay aporte externo de energía, lo que sale de uno es lo que entra en el otro

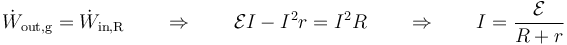
Vemos que la ley de Ohm generalizada es equivalente a la ley de conservación de la energía para este caso.

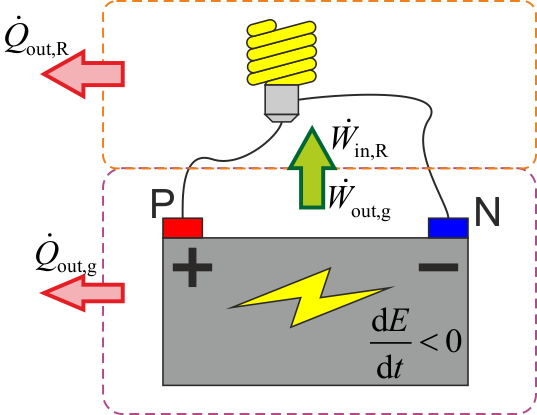
¿De donde procede la potencia eléctrica que sale del generador? De la fuerza no eléctrica que está actuando sobre las cargas. Como la bomba de agua, este fuerza está subiendo las cargas de potencial, realizando un cierto trabajo. Puede ser trabajo mecánico, o puede provenir de la liberación de energía almacenada en los enlaces químicos. De acuerdo con el primer principio de la termodinámica

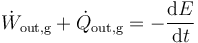
Del generador escapa tanto energía eléctrica (como flujo de trabajo) como calor (pues por la resistencia interna se calienta y empieza a radiar calor). Esa energía procede de la energía total almacenada en el sistema. En un sistema aislado, esta energía termina agotándose y la corriente se detiene. Esto es lo que ocurre al descargarse una pila. En la batería de un automóvil se produce una recarga continua a partir de la energía procedente de la combustión de la gasolina. Si no hay recarga (como ocurre al dejarse las luces encendidas por la noche) la batería se termina agotando.

El caso de un generador eléctrico mecánico (como uno unido a una turbina o un aerogenerador), no se está consumiendo energía almacenada, sino que el trabajo eléctrico que sale procede del trabajo mecánico que entra.