Gas calentado por una resistencia Primera Convocatoria Ordinaria 2010/11 (F2GIA)
De Laplace
Contenido |
1 Enunciado
En un recipiente cerrado de paredes fijas y adiabáticas se tienen 2.00 moles de un gas ideal diatómico, a una
presión de 100 kPa y una temperatura de 25.0 oC. En el interior del volumen hay una resistencia
de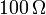 
por la que circula durante 1.00 minuto una corriente de 
.
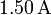Dato: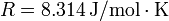 
- Calcula el volumen del gas.
- Calcula la variación de energía interna del gas.
- ¿Cual es la presión final del gas?
2 Solución
2.1 Volumen del gas
A partir de la ecuación de estado de un gas ideal calculamos el volumen ocupado por el gas
2.2 Variación de energía interna del gas
Al circular corriente por la resistencia, se disipa calor que se transfiere al gas. Por otro lado las paredes del recipiente son rígidas, con lo que el gas no sufre ningún trabajo. Así pues, en el Primer Principio de la Termodinámica tenemos
ΔU = Q + W = Qres + 0 = Qres
Para el gas, el proceso no es adiabático. Las paredes adiabáticas lo único que hacen es asegurar que todo el calor producido en la resistencia es absorbido por el gas.
La potencia disipada en la resistencia es
Como está encendida durante un minuto, el calor total transferido al gas es
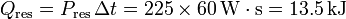
Así la variación de energía interna es
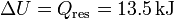
2.3 Presión final del gas
Podemos calcular la variación de temperatura del gas en el proceso. Para cualquier proceso la variación de energía interna de un gas ideal es
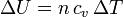
donde n es el número de moles y cv es el calor específico molar a volumen constante. El enunciado dice que es un gas diatómico, por lo que 
. Usando el resultado del apartado anterior tenemo
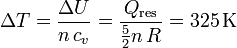
La temperatura final es
Podemos determinar el valor de la presión en el estado final usando la ecuación de estado de los gases ideales. Teniendo en cuenta que el volumen es constante tenemos
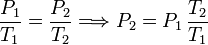
Sustituyendo los valores numéricos tenemos
