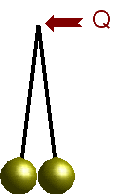Funcionamiento de un electroscopio elemental

De Laplace

1 Enunciado

Un electroscopio mide la carga por la desviación angular de dos esferas idénticas conductoras, suspendidas por cuerdas aislantes de masas despreciables y longitud $L$ . Cada esfera tiene una masa $m$ y está sometida a la gravedad $g$ . Las cargas pueden considerarse como puntuales e iguales entre sí. Halle la ecuación que liga el semiángulo $θ$ con el valor de la carga total $Q$ depositada en las esferas.

Suponga que la masa de cada esfera es $m = 10 - 4$ kg y la longitud del cable del que penden es 20 cm. Admita asimismo que los ángulos de desviación pueden medirse como mucho con una precisión de 1°. ¿Cuál es la carga mínima que puede medirse con este aparato? ¿Y la carga máxima?

2 Solución

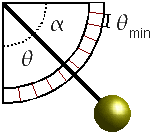
Si las bolas están descargadas la configuración del electroscopio es la que se muestra en la figura. Al depositar una carga $Q$ , como las dos esferas son idénticas y los dos hilos también, la carga se distribuye por igual en las dos esferas. Es decir, cada una de ellas adquiere una carga $Q / 2$ . Como las cargas de las esferas son iguales y del mismo signo, se repelen, con lo que aumenta el ángulo $θ$ que forman los hilos con la vertical.

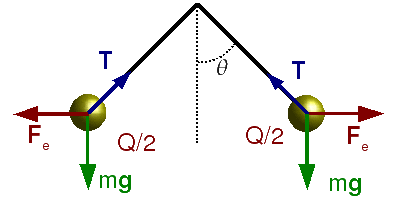
La figura siguiente muestra el estado de equilibrio del sistema. Sobre cada bola actúan tres fuerzas, a saber: el peso, 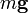$m\mathbf{g}$ la fuerza eléctrica debida a la otra esfera, 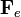$\mathbf{F}_e$ y la tensión de la cuerda, 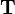$\mathbf{T}$ . Para resolver el problema supondremos que las esferas son cargas puntuales, esto es, que su radio es mucho menor que la distancia que separa las esferas en todo instante. Esto es bastante cierto cuando el ángulo $θ$ es grande, pero no tanto cuando las dos esferas están muy próximas. De todos modos, las esferas de las figuras son mucho más grandes que las que se usan en la práctica.

Para encontrar el valor de equilibrio del ángulo $θ$ vamos a examinar las fuerzas que actúan sobre una de las bolas. Es indiferente cual de ellas consideremos, pues las fuerzas son simétricas respecto a la línea central.

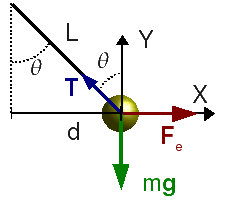
Escogemos los ejes como se indica en la figura de la izquierda. Como consideramos la esfera una carga puntual, la condición de equilibrio estático es que la suma de fuerza sobre ella sea nula. Vamos a descomponer las tres fuerzas que actúan sobre la esfera

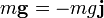
Peso: $m\mathbf{g} =-mg\mathbf{j}$

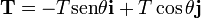
Tensión: $\mathbf{T} =-T\mathrm{sen}\theta\mathbf{i}+T\cos\theta\mathbf{j}$

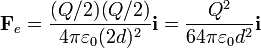
Fuerza eléctrica: $\mathbf{F}_e =\frac{(Q/2)(Q/2)}{4\pi\varepsilon_0(2d)^2}\mathbf{i}=\frac{Q^2}{64\pi\varepsilon_0d^2}\mathbf{i}$

Para calcular 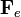$\mathbf{F}_e$ hemos usado la ley de Coulomb. La carga de cada esfera es $Q / 2$ y la distancia entre ellas es $2 d$ , siendo $d$ la distancia indicada en el dibujo. Como la suma vectorial debe ser cero, obtenemos dos ecuaciones escalares

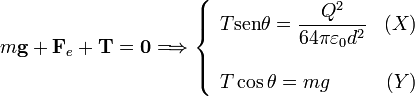
$m\mathbf{g}+\mathbf{F}_e+\mathbf{T}=\mathbf{0}\Longrightarrow \left\{ \begin{array}{lr} \displaystyle T\mathrm{sen}\theta=\frac{Q^2}{64\pi\varepsilon_0d^2}& (X)\\ & \\ T\cos\theta= mg & (Y) \end{array} \right.$

Eliminamos la tensión del hilo dividiendo las dos ecuaciones entre sí.

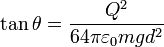
$\tan\theta=\frac{Q^2}{64\pi\varepsilon_0 mg d^2}$

Por otro lado, la distancia $d$ puede escribirse en función de la longitud del hilo y del semiángulo $θ$

$d = L senθ$

Por tanto, la expresión final que relaciona el ángulo con la carga es

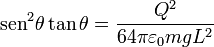
$\mathrm{sen}^2\theta\tan\theta=\frac{Q^2}{64\pi\varepsilon_0 mg L^2}$

No podemos despejar el valor del ángulo en función de la carga porque la ecuación es trascendente. Pero si podemos usar esta expresión para medir la carga depositada en las esferas en función del ángulo y el resto de parámetros. Nos queda

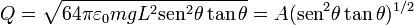
$Q=\sqrt{64\pi\varepsilon_0mgL^2\mathrm{sen}^2\theta\tan\theta}=A(\mathrm{sen}^2\theta\tan\theta)^{1/2}$

siendo la constante

$A=(64\pi\varepsilon_0mgL^2)^{1/2}$

la que recoge el valor de los parámetros del electroscopio. Con los valores numéricos del problema se tiene

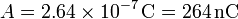
$A=2.64\times10^{-7}\,\mathrm{C}=264\,\mathrm{nC}$

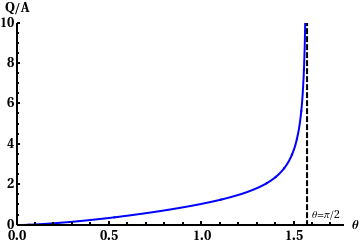
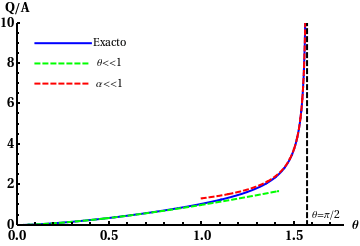
El valor de $A$ da una idea del orden de magnitud de la carga que puede medir este electroscopio. La figura de la derecha muestra como varía el cociente $Q / A$ en función del ángulo $θ$ . Suponiendo que las cargas sean puntuales, cuando la carga depositada tiende a cero también lo hace el ángulo. Por otro lado, el ángulo máximo que se puede medir es $π / 2$ , es decir, que las dos esferas estén en el mismo plano y los hilos estén completamente horizontales. Se observa en la gráfica que la carga tiende a infinito cuando el ángulo tiende a $π / 2$ , pues por muy grande que sea la carga depositada el ángulo no puede sobrepasar $π / 2$ .

Ahora bien, en la práctica no se puede medir un ángulo arbitrariamente pequeño. Típicamente, el electroscopio se coloca sobre un cuadrante, como se indica en la figura de la izquierda. Por tanto se puede medir una ángulo mínimo, $θ min$ y un ángulo máximo $π / 2 - θ min$ . Para evaluar estos límites vamos a encontrar las expresiones asintóticas de la expresión que da la carga en función del ángulo para valores próximos a $θ = 0$ y $θ = π / 2$ .

Ángulos próximos a $θ = 0$

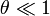En este límite se cumple que el ángulo es muy pequeño, $\theta\ll1$ . Entonces se pueden usar los desarrollos en serie de Taylor del seno y del coseno

$\mathrm{sen}\theta\simeq\theta\,\,\,\,\,\,\,\,\,\,\tan\theta\simeq\theta$

La carga es entonces

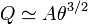
$Q\simeq A\theta^{3/2}$

Si el ángulo mínimo es

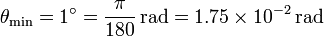
$\theta_{\mathrm{min}}=1^{\circ}=\frac{\pi}{180}\,\mathrm{rad}=1.75\times10^{-2}\,\mathrm{rad}$

se cumple la condición de ángulo pequeño, y se puede usar la expresión asintótica. Obtenemos que la carga mínima que se puede medir es

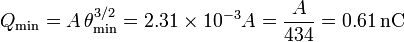
$Q_{\mathrm{min}} = A\,\theta_{\mathrm{min}}^{3/2}=2.31\times10^{-3}A=\frac{A}{434}=0.61\,\mathrm{nC}$

Ángulos próximos a $θ = π / 2$

En este caso es mejor trabajar con el ángulo complementario de $θ$

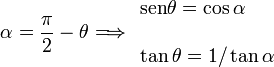
$\alpha=\frac{\pi}{2}-\theta\Longrightarrow \begin{array}{l} \mathrm{sen}{\theta}=\cos\alpha\\ \\ \tan\theta=1/\tan\alpha \end{array}$

La carga en función del ángulo $α$ es

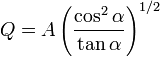
$Q=A\left(\frac{\cos^2\alpha}{\tan\alpha}\right)^{1/2}$

Cuando $θ$ es próximo a $π / 2$ se cumple 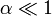$\alpha\ll1$ , entonces

$\cos\alpha\simeq1\,\,\,\,\,\,\,\,\,\,\tan\alpha\simeq\alpha$

y la carga es

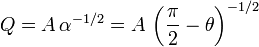
$Q=A\,\alpha^{-1/2}=A\,\left(\frac{\pi}{2}-\theta\right)^{-1/2}$

La carga máxima se obtiene cuando $α = θ min$

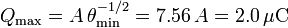
$Q_{\mathrm{max}}=A\,\theta_{\mathrm{min}}^{-1/2}=7.56\,A=2.0\,\mathrm{\mu C}$

La figura muestra como depende la carga depositada en el electroscopio del ángulo. La línea azul es la solución exacta, la línea verde muestra la aproximación cuando el ángulo es pequeño, mientras que la línea roja es la aproximación válida cuando el ángulo esta próximo a $π / 2$ . Puede observarse que las expresiones aproximadas son válidas en rangos muy grandes del ángulo.

Funcionamiento de un electroscopio elemental

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES