Flujo del campo eléctrico de un cubo (GIOI)
De Laplace
1 Enunciado
![]() Un cubo de arista b contiene una carga Q0 distribuida uniformemente en su volumen. No hay más cargas en el sistema. Sea S una superficie esférica de radio b centrada en uno de los vértices del cubo. ¿Cuánto vale el flujo del campo eléctrico a través de S?
Un cubo de arista b contiene una carga Q0 distribuida uniformemente en su volumen. No hay más cargas en el sistema. Sea S una superficie esférica de radio b centrada en uno de los vértices del cubo. ¿Cuánto vale el flujo del campo eléctrico a través de S?
2 Solución
De acuerdo con la ley de Gauss
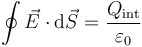
por lo que el flujo que nos piden se reduce a calcular la carga encerrada por la superficie esférica.
La esfera corta al cubo de tal forma que el volumen donde hay carga es 1/8 de la esfera. Tres caras del cubo están sobre los planos coordenados y delimitan un octante (de la misma manera que hay cuatro cuadrantes en el plano, hay ocho octantes en el espacio).
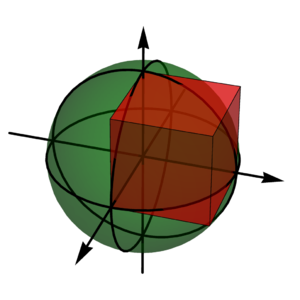
Por tanto la carga encerrada es
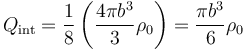
La densidad de carga la sacamos de dividir la carga total del cubo por el volumen del cubo
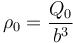
lo que nos da el flujo del campo eléctrico






