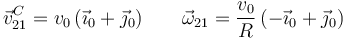F1 GIA SPC 2015, Disco rodando sin deslizar ni pivotar
De Laplace
1 Enunciado
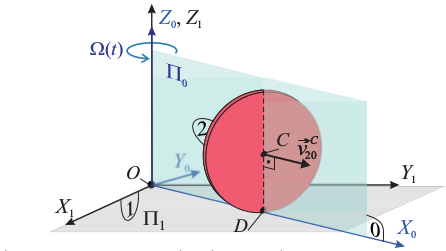
Un disco de radio R (sólido "2"), se mueve siempre en contacto (puntual) con un
plano Π1 = OX1Y1 (sólido "1") y de manera que, en cada
instante, el radio CD desde el centro C del disco
hasta el punto D en contacto con Π1, es
perpendicular a dicho plano. El movimiento del disco respecto del plano
Π1 se caracteriza porque no presenta ni deslizamiento en el
punto D de contacto, ni tampoco pivotamiento con respecto a dicho
plano. Para describir más fácilmente el movimiento, se introduce un sistema de
referencia intermedio (sólido "0" ), tal que OZ0 = OZ1, y que el
plano 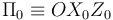 contenga en cada instante al radio
CD. El centro C del disco realiza, en el plano
Π0, un movimiento rectilíneo uniforme por el cuál se aleja del
eje OZ0,1 a velocidad constante v0; mientras,
Π0 realiza una rotación permanente en torno a dicho eje, en
sentido antihorario y con velocidad angular variable Ω(t) = v0 / (R + v0t). En el instante inicial, t = 0, el centro del
disco se encuentra en la posición dada por el segmento orientado
contenga en cada instante al radio
CD. El centro C del disco realiza, en el plano
Π0, un movimiento rectilíneo uniforme por el cuál se aleja del
eje OZ0,1 a velocidad constante v0; mientras,
Π0 realiza una rotación permanente en torno a dicho eje, en
sentido antihorario y con velocidad angular variable Ω(t) = v0 / (R + v0t). En el instante inicial, t = 0, el centro del
disco se encuentra en la posición dada por el segmento orientado
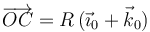 ; es decir, a una
distancia R del eje OZ0,1.
; es decir, a una
distancia R del eje OZ0,1.
- Encuentre la reducción cinemática del movimiento {21} en el punto C.
2 Solución
Tal como se indica en el dibujo tenemos
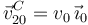
El enunciado dice que el disco no desliza en el punto D, por tanto
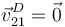
También dice que el disco no pivota, es decir, el vector rotación  no
tiene componente perpendicular al plano
no
tiene componente perpendicular al plano
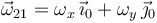
Del enunciado también sabemos que
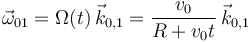
También sabemos que los puntos del eje OZ0,1 no se mueven en el movimiento {01}, esto es
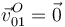
Vamos a calcular 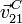 usando la composición de movimientos {21} = {20} +
{01}. Tenemos
usando la composición de movimientos {21} = {20} +
{01}. Tenemos
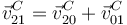
Tenemos ya el el primer sumando. Usamos el teorema de Chasles aplicado al movimiento {01} para calcular el segundo
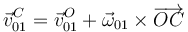
Si en el instante inicial 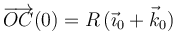 y el
punto C realiza un movimiento rectilíneo uniforme sobre el eje OX0
tenemos
y el
punto C realiza un movimiento rectilíneo uniforme sobre el eje OX0
tenemos
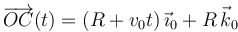
Haciendo el producto vectorial
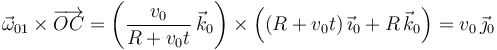
y por tanto
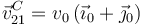
Ahora aplicamos el teorema de Chasles al movimiento {21} para relacionar las velocidades en los puntos C y D.
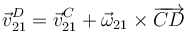
El vector geométrico es 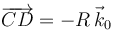 . Tenemos
. Tenemos
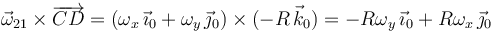
Tenemos entonces
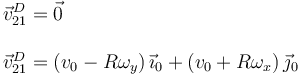
De aquí obtenemos
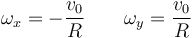
La reducción buscada es