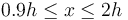F1 GIA PPC 2013, Equilibrio de una masa sobre un plano inclinado con un muelle

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

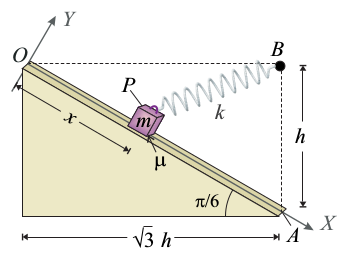
Un plano inclinado de longitud $2 h$ , forma un ángulo de $30 o$ con la horizontal, de manera que entre sus puntos extremos $O$ y $A$ hay una diferencia de altura de valor $h$ . También a un altura $h$ sobre la vertical de $A$ existe un punto $B$ en el cuál se fija un resorte ideal, de longitud natural nula y constante recuperadora $K$ . El otro extremo del resorte se conecta a un cuerpo pesado, de masa $m$ , que puede considerarse puntual, y que se coloca sobre la superficie del plano inclinado. El contacto con el plano es rugoso con un coeficiente de rozamiento estático $μ$ .

Dibuje el diagrama de cuerpo libre de la partícula.
Determina la fuerza de rozamiento en situación de equilibrio estático.
Si 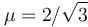$\mu=2/\sqrt{3}$ , ¿qué condición ha de verificar la masa de la partícula para que el punto medio de la rampa sea una posición de equilibrio?
A la condición del apartado anterior añada que la masa es $m = 3.2 K h / g$ . ¿Hasta qué distancia $x e q$ del extremo superior $O$ se mantendrá la partícula en equilibrio sobre la rampa?

2 Solución

2.1 Fuerzas sobre la partícula

La imagen de la derecha muestra las fuerzas que actúan sobre la masa, a saber, el peso, la fuerza del muelle, la reacción normal del plano y la fuerza de rozamiento. Expresamos todas estas fuerzas en los ejes de la figura.

El peso es

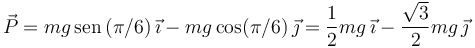
$\vec{P} = mg\,\mathrm{sen}\,(\pi/6)\,\vec{\imath} - mg\cos(\pi/6)\,\vec{\jmath} = \dfrac{1}{2}mg\,\vec{\imath} - \dfrac{\sqrt{3}}{2}mg\,\vec{\jmath}$

La reacción normal y la fuerza de rozamiento son

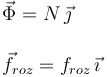
$\begin{array}{l} \vec{\Phi} = N\,\vec{\jmath}\\ \\ \vec{f}_{roz} = f_{roz}\,\vec{\imath} \end{array}$

Hay que recordar que $f r o z$ puede ser negativo o positivo. Si es negativo 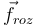$\vec{f}_{roz}$ apunta hacia la izquierda, como se ve en la figura, mientras que si es positivo apunta hacia la derecha.

El muelle tiene longitud natural nula, por tanto la fuerza que ejerce sobre la partícula es

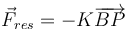
$\vec{F}_{res} = -K\overrightarrow{BP}$

El vector de posición del punto $P$ es

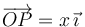
$\overrightarrow{OP} = x\,\vec{\imath}$

Para el punto $B$ podemos usar que la longitud del segmento 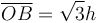$\overline{OB}=\sqrt{3}h$ , y que este segmento forma un ángulo $π / 6$ con el eje $O X$ (el plano inclinado). Entonces

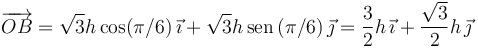
$\overrightarrow{OB} = \sqrt{3}h\cos(\pi/6)\,\vec{\imath} + \sqrt{3}h\,\mathrm{sen}\,(\pi/6)\,\vec{\jmath} = \dfrac{3}{2}h\,\vec{\imath} + \dfrac{\sqrt{3}}{2}h\,\vec{\jmath}$

Entonces la fuerza que ejerce el muelle es

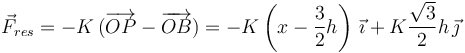
$\vec{F}_{res} = -K\,(\overrightarrow{OP} - \overrightarrow{OB}) = -K \left( x - \dfrac{3}{2}h\right)\,\vec{\imath} + K\dfrac{\sqrt{3}}{2}h\,\vec{\jmath}$

2.2 Fuerzas en equilibrio

En equilibrio la suma de fuerzas debe ser cero

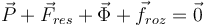
$\vec{P} + \vec{F}_{res} + \vec{\Phi} + \vec{f}_{roz} = \vec{0}$

Esto nos da dos ecuaciones, una por cada componente

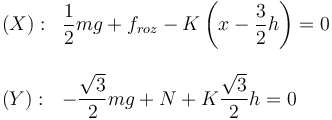
$\begin{array}{ll} (X): & \dfrac{1}{2}mg + f_{roz} -K\left(x-\dfrac{3}{2}h\right) = 0\\ &\\ (Y): & -\dfrac{\sqrt{3}}{2}mg + N + K\dfrac{\sqrt{3}}{2}h = 0 \end{array}$

Tenemos tres incógnitas: $x$ , $N$ y $f r o z$ , y sólo dos ecuaciones. Esto se debe a que hay varias posiciones de equilibrio. Según sea el valor de $x$ , la fuerza de rozamiento se ajusta para intentar mantener el equilibrio.

El enunciado nos dice que consideremos el caso en que la partícula esta en el medio de la rampa, es decir, $x = h$ . Con ese dato, podemos determinar los valores de $N$ y $f r o z$ en esa situación

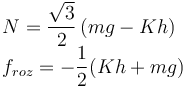
$\begin{array}{l} N = \dfrac{\sqrt{3}}{2}\left(mg-Kh\right) \\ f_{roz} = -\dfrac{1}{2} ( Kh + mg ) \end{array}$

La fuerza de rozamiento apunta hacia la izquierda, como se indica en el dibujo.

La fuerza normal sólo actúa si la fuerza neta activa sobre la partícula intenta hacerla penetrar en el plano inclinado. Si el muelle domina y hace que la partícula se separe del plano la fuerza normal ya no es necesario. Así pues, la condición para que la partícula permanezca sobre el plano es

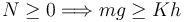
$N\geq 0 \Longrightarrow mg \geq Kh$

2.3 Condición para que haya equilibrio

Observemos que el coeficiente de rozamiento no ha aparecido hasta ahora. ¿Cómo es posible? En general, el módulo de la fuerza de rozamiento no es $μ$ por la normal. El valor de la fuerza de rozamiento es el que haga falta para que la partícula no se mueva. Ocurre que la fuerza de rozamiento no puede tener cualquier valor: tiene un valor máximo. Si la magnitud que necesita tener la fuerza de rozamiento es mayor que este máximo, la fuerza de rozamiento no puede llegar a él, y la partícula se mueve. Así pues, para que haya equilibrio debe cumplirse la condición

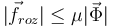
$|\vec{f}_{roz}| \leq \mu|\vec{\Phi}|$

Si consideramos la situación en que la partícula está en el centro de la rampa podemos usar las fuerzas calculadas en el apartado anterior. La condición de equilibrio es entonces

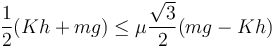
$\dfrac{1}{2}(Kh+mg) \leq \mu\dfrac{\sqrt{3}}{2}(mg-Kh)$

Esta desigualdad se puede interpretar como una condición sobre el valor de la masa

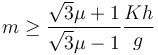
$m \geq \dfrac{\sqrt{3}\mu + 1}{\sqrt{3}\mu - 1}\dfrac{Kh}{g}$

Sustituyendo el valor 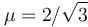$\mu = 2/\sqrt{3}$ obtenemos la condición

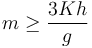
$m\geq \dfrac{3Kh}{g}$

2.4 Posición más alta de equilibrio

Ahora no fijamos la posición de la partícula. Podemos considerar que la fuerza de rozamiento necesaria para que haya equilibrio es una función de $x$ , dada por la componente $X$ de las ecuaciones de equilibrio

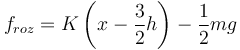
$f_{roz} = K\left(x-\dfrac{3}{2}h\right) - \dfrac{1}{2}mg$

La pregunta es, ¿hasta que valor de $x$ esta fuerza de rozamiento es menor que el valor máximo que puede alcanzar?. La condición de equilibrio ahora se expresa como

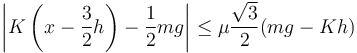
$\left|K\left(x-\dfrac{3}{2}h\right) - \dfrac{1}{2}mg\right| \leq \mu\dfrac{\sqrt{3}}{2}(mg-Kh)$

Sustituimos los valores de $μ$ y $m$ dados en el enunciado. La condición queda

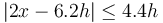
$|2x-6.2h| \leq 4.4h$

El termino de la izquierda puede ser positivo o negativo. Si es positivo podemos quitar las barra de valor absoluto y obtenemos que, para que el equilibrio sea posible, debe ocurrir que

$2x\leq 10.6h \Longrightarrow x \leq 5.4h$

La rampa tiene una longitud $2 h$ . Eso quiere decir todos los puntos de la rampa verifican esta condición.

Si el primer término es negativo, tomar valor absoluto equivale a aplicar un signo menos. Nos queda

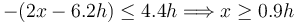
$-(2x-6.2h)\leq 4.4h \Longrightarrow x \geq 0.9 h$

Así pues, las posiciones de equilibrio sobre la rampa están en el intervalo

$0.9h \leq x \leq 2h$

F1 GIA PPC 2013, Equilibrio de una masa sobre un plano inclinado con un muelle

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas sobre la partícula

2.2 Fuerzas en equilibrio

2.3 Condición para que haya equilibrio

2.4 Posición más alta de equilibrio

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES