Expansión de un gas en contacto con agua caliente Primera Convocatoria Ordinaria 2010/11 (F2GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Tenemos un recipiente adiabático con una tapa superior que puede desplazarse como un pistón. El volumen interior está dividido en dos recintos conectados por una pared fija diaterma (que deja pasar el calor). En el recinto inferior hay 500 g de agua líquida a una temperatura $T_a=100\,\mathrm{^oC}$ . 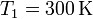El recinto superior está ocupado por un gas ideal diatómico que ocupa inicialmente un volumen $V_1 = 0.500\,\mathrm{m^3}$ a una temperatura $T_1=300\,\mathrm{K}$ y una presión $P_1=300\,\mathrm{kPa}$ . En el exterior la presión es $P_0=100\,\mathrm{kPa}$ .

Calcula la temperatura y el volumen finales del gas cuando se llega a la situación de equilibrio.
¿Cuánto es el trabajo realizado sobre el gas?
¿Cuánto vale el calor cedido por la masa de agua?
¿Cuál es la variación de energía interna del sistema gas-agua?

Datos: Constante universal de los gases ideales $R=8.31\,\mathrm{J/\mathrm{mol}\cdot K}$ , calor específico del agua líquida $c_a=4.18\,\mathrm{KJ/Kg\cdot K}$ .

2 Solución

2.1 Estado final de equilibrio

El gas puede intercambiar calor con el volumen de agua, pero no trabajo, pues la pared que los separa es fija. Por otro lado, el gas puede intercambiar trabajo con el exterior, debido a que la tapa superior puede desplazarse, pero no puede intercambiar calor, pues las paredes son adiabáticas.

Así pues, el gas estará en equilibrio cuando esté a la misma temperatura que la masa de agua y a la misma presión que el exterior. Es decir, en el estado de equilibrio la presión del gas es $P 0$ y la temperatura final es $T e q$ . Para el gas el proceso no es adiabático y además es irreversible, pues la diferencia entre la presión interior inicial del gas y la exterior es muy grande. La figura indica las interacciones entre el gas y el agua y el gas y el exterior. Aplicando el Primer Principio de la Termodinámica al proceso que sufre el gas tenemos

$\Delta U_g =W_g + Q_{a\to g}$

Al ser un gas ideal diatómico, la variación de energía interna del gas es

$\Delta U_g = n\,c_v(T_{eq}-T_1) = \dfrac{5}{2}\,n\,R\,(T_{eq} - T_1) = \dfrac{5}{2}\,n\,R\,T_{eq} - \dfrac{5}{2}\,n\,R\,T_1 = \dfrac{5}{2}\,n\,R\,T_{eq} - \dfrac{5}{2}\,P_1\,V_1$

Hemos usado que para un gas ideal $c_v = 5\,R/2$ y la ecuación de estado del gas ideal: $n\,R\,T_1 = P_1\,V_1$ .

El trabajo realizado sobre el gas puede calcularse pues la presión externa es constante

$W_g = -P_0\,(V_{eq}-V_1) = -P_0\,V_{eq} + P_0\,V_1 = -n\,R\,T_{eq} + P_0\,V_1$

De nuevo hemos usado la ecuación de estado del gas ideal en el estado final de equilibrio.

Por último, el calor que el agua cede al pasar de su temperatura inicial a la final es

$Q_{g\to a} = m_a\,c_a\,(T_{eq} - T_a)$

El calor que absorbe el gas es el mismo cambiado de signo

$Q_{a\to g} = - Q_{g\to a} = -m_a\,c_a\,T_{eq} + m_a\,c_a\,T_a$

Sustituyendo estas expresiones en el Primer Principio, obtenemos una ecuación cuya única incógnita es la temperatura de equilibrio del gas

$\dfrac{5}{2}\,n\,R\,T_{eq} - \dfrac{5}{2}\,P_1\,V_1 = -n\,R\,T_{eq} + P_0\,V_1 -m_a\,c_a\,T_{eq} + m_a\,c_a\,T_a$

Despejando la temperatura de equilibrio tenemos

$T_{eq} = \dfrac{\displaystyle \dfrac{5}{2}\,P_1\,V_1 + P_0\,V_1 + m_a\,c_a\,T_a}{\displaystyle\dfrac{7}{2}\,n\,R + m_a\,c_a}$

Usando de nuevo la ecuación del gas ideal en el estado inicial del gas tenemos

$n\,R = \dfrac{P_1\,V_1}{T_1}$

Sustituyendo los valores numéricos obtenemos

$T_{eq} = 314\,\mathrm{K} = 40.9\,\mathrm{^{\circ}C}$

El volumen final lo obtenemos de la ecuación del gas ideal

$V_{eq} = \dfrac{n\,R\,T_{eq}}{P_0} = \dfrac{ P_1\,V_1\,T_{eq}}{P_0\,T_1} = 0.524\,\mathrm{m^3}$

2.2 Trabajo realizado sobre el gas

Este trabajo es

$W_g = -P_0\,(V_{eq}-V_1) = 2.40\,\mathrm{kJ}$

2.3 Calor cedido por la masa de agua

Usando la expresión del apartado 1 tenemo

$Q_{a\to g} = -m_a\,c_a(T_{eq}-T_a) = -124\,\mathrm{kJ}$

2.4 Variación de energía interna del sistema gas+agua

Considerando conjuntamente el gas y el agua, es sistema es adiabático, por lo que el único intercambio de energía es trabajo realizado sobre el gas. Por tanto

$\Delta U_{ag} = W_g = 2.40\,\mathrm{kJ}$

Expansión de un gas en contacto con agua caliente Primera Convocatoria Ordinaria 2010/11 (F2GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Estado final de equilibrio

2.2 Trabajo realizado sobre el gas

2.3 Calor cedido por la masa de agua

2.4 Variación de energía interna del sistema gas+agua

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES