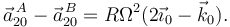De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

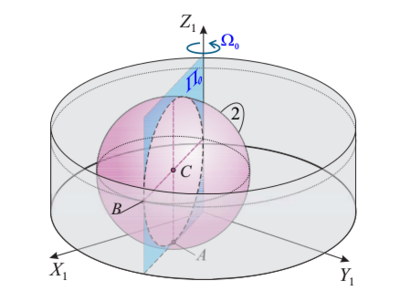
Una esfera de radio $R$ (sólido "2") se mueve en el interior de un recipiente cilíndrico de radio $2 R$ (sólido "1"). El movimiento es tal que, en todo momento, la esfera rueda sin deslizar en los dos puntos $A$ y $B$ en contacto con la superficie cilíndrica (ver figura). El centro $C$ de la esfera realiza un movimiento circular uniforme. Introducimos un sólido intermedio $O X 0 Y 0 Z 0$ , de modo que el eje $O Z 0$ coincide en todo instante con $O Z 1$ , y el plano $O X 0 Z 0$ contiene siempre al centro de la esfera $C$ . Este plano gira alrededor de $O Z 0$ , en sentido antihorario y con velocidad angular constante $Ω$ .

Obtenga reducciones cinemáticas de todos los movimientos relativos {01}, {20} y {21}, así como sus derivadas instantáneas. Indique que tipo de movimiento son.
¿Cómo son los movimientos de pivotamiento y rodadura del sólido "2" respecto del "1" en los puntos que ocupan las posiciones de contacto $A$ y $B$ ?.
Calcula $\vec{a}^{\,A}_{21}- \vec{a}^{\,B}_{21}$ y $\vec{a}^{\,A}_{20}- \vec{a}^{\,B}_{20}$ .

2 Solución

2.1 Análisis de la información cinemática en el enunciado

La esfera no desliza en los puntos $A$ y $B$ , por tanto

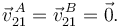
$\vec{v}^{\,A}_{21} =\vec{v}^{\,B}_{21} = \vec{0}.$

Entonces

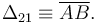
$\Delta_{21} \equiv \overline{AB}.$

El plano $O X 0 Z 0$ realiza una rotación de eje permanente con velocidad angular constante. Entonces

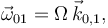
$\vec{\omega}_{01} = \Omega\,\vec{k}_{0,1},$

y además

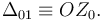
$\Delta_{01} \equiv OZ_0.$

El punto $C$ es un punto fijo común de la esfera y el sólido "0". Por tanto

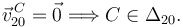
$\vec{v}^{\,C}_{20} = \vec{0} \Longrightarrow C\in\Delta_{20}.$

Como se ve en la figura de la derecha. los ejes $Δ 21$ y $Δ 01$ se cortan en el punto $I$ . Entonces 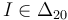$I\in\Delta_{20}$ . Y por tanto

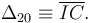
$\Delta_{20} \equiv \overline{IC}.$

2.2 Reducciones cinemáticas

2.2.1 Movimiento {01}

Tenemos

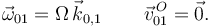
$\vec{\omega}_{01} = \Omega\,\vec{k}_{0,1}\,\qquad \vec{v}^{\,O}_{01} = \vec{0}.$

La velocidad de este movimiento es cero en cualquier punto del eje $O Z 0$ . La derivada temporal es

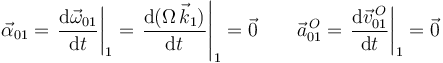
$\vec{\alpha}_{01} = \left.\dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1 = \left.\dfrac{\mathrm{d}(\Omega\,\vec{k}_1)}{\mathrm{d}t}\right|_1 = \vec{0} \qquad \vec{a}^{\,O}_{01} = \left.\dfrac{\mathrm{d}\vec{v}^{\,O}_{01}}{\mathrm{d}t}\right|_1 = \vec{0}$

Es una rotación de eje permanente. Por eso la velocidad y aceleración de todos los puntos del eje es nula en todo instante.

2.2.2 Movimiento {21}

Sabemos que 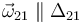$\vec{\omega}_{21}\parallel \Delta_{21}$ , entonces

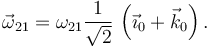
$\vec{\omega}_{21} = \omega_{21} \dfrac{1}{\sqrt{2}}\,\left(\vec{\imath}_0 +\vec{k}_0\right).$

La velocidad en $A$ es

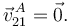
$\vec{v}^{\,A}_{21} = \vec{0}.$

Y en el centro de la esfera es

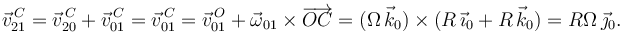
$\vec{v}^{\,C}_{21} = \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01} = \vec{v}^{\,C}_{01} =\vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OC} = (\Omega\,\vec{k}_0)\times(R\,\vec{\imath}_0 + R\,\vec{k}_0) = R\Omega\,\vec{\jmath}_0.$

Por otro lado,

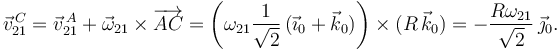
$\vec{v}^{\,C}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AC} = \left(\omega_{21}\dfrac{1}{\sqrt{2}}\,(\vec{\imath}_0+\vec{k}_0)\right)\times(R\,\vec{k}_0) = -\dfrac{R\omega_{21}}{\sqrt{2}}\,\vec{\jmath}_0.$

Comparando obtenemos

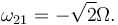
$\omega_{21} = -\sqrt{2}\Omega.$

Una reducción cinemática es

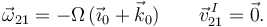
$\vec{\omega}_{21} = -\Omega\,(\vec{\imath}_0 + \vec{k}_0) \qquad \vec{v}^{\,I}_{21} = \vec{0}.$

Calculamos la derivada del vector rotación, utilizando la fórmula de Poisson

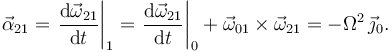
$\vec{\alpha}_{21} = \left.\dfrac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1 = \left.\dfrac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_0 + \vec{\omega}_{01}\times\vec{\omega}_{21}= -\Omega^2\,\vec{\jmath}_0.$

El punto $I$ está siempre en el eje $Δ 21$ , por tanto su velocidad es siempre nula. Entonces

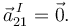
$\vec{a}^{\,I}_{21} = \vec{0}.$

El movimiento es una rotación pura de eje instantáneo. El eje $Δ 21$ se mueve respecto al sólido "1".

2.2.3 Movimiento {20}

Usamos las leyes de composición del movimiento {21}={20}+{01}

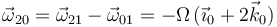
$\vec{\omega}_{20} = \vec{\omega}_{21} - \vec{\omega}_{01} = -\Omega\,(\vec{\imath}_0+2\vec{k}_0)$

Una posible reducción cinemática es

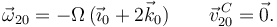
$\vec{\omega}_{20} = -\Omega\,(\vec{\imath}_0+2\vec{k}_0) \qquad \vec{v}^{\,C}_{20} = \vec{0}.$

Derivamos el vector rotación

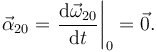
$\vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0 =\vec{0}.$

Y

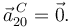
$\vec{a}^{\,C}_{20} = \vec{0}.$

El movimiento es una rotación pura de eje permanente, pues el eje $Δ 20$ pasa siempre por los mismos puntos del sólido "0".

2.3 Pivotamiento y rodadura

En un punto dado el pivotamiento viene dado por la componente perpendicular a la superficie del vector rotación. En el punto $A$ el vector normal es 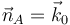$\vec{n}_A = \vec{k}_0$ , mientras que en el punto $B$ es 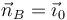$\vec{n}_B=\vec{\imath}_0$ . Entonces

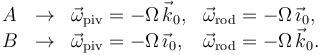
$\begin{array}{lcll} A & \to & \vec{\omega}_{\mathrm{piv}} = -\Omega\,\vec{k}_0, & \vec{\omega}_{\mathrm{rod}} = -\Omega\,\vec{\imath}_0,\\ B & \to & \vec{\omega}_{\mathrm{piv}} = -\Omega\,\vec{\imath}_0, & \vec{\omega}_{\mathrm{rod}} = -\Omega\,\vec{k}_0. \end{array}$

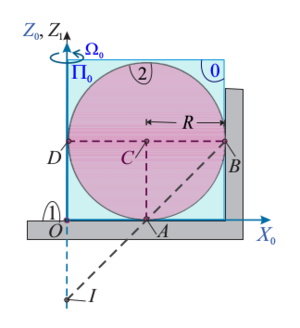
2.4 Cálculo de diferencias de aceleraciones

Usamos en cada caso la ecuación del campo de aceleraciones del movimiento correspondiente. Para el primer caso

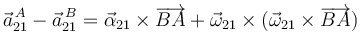
$\vec{a}^{\,A}_{21} - \vec{a}^{\,B}_{21} = \vec{\alpha}_{21}\times\overrightarrow{BA} + \vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{BA})$

El segundo término es nulo pues 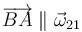$\overrightarrow{BA} \parallel \vec{\omega}_{21}$ . El vector geométrico es

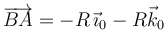
$\overrightarrow{BA} = -R\,\vec{\imath}_0 - R\vec{k}_0$

Entonces

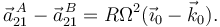
$\vec{a}^{\,A}_{21} - \vec{a}^{\,B}_{21} = R\Omega^2(\vec{\imath}_0 - \vec{k}_0).$

Para el otro caso

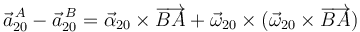
$\vec{a}^{\,A}_{20} - \vec{a}^{\,B}_{20} = \vec{\alpha}_{20}\times\overrightarrow{BA} + \vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{BA})$

Ahora el primer término es nulo, pues 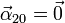$\vec{\alpha}_{20}=\vec{0}$ . Operando llegamos a

$\vec{a}^{\,A}_{20} - \vec{a}^{\,B}_{20} = R\Omega^2(2\vec{\imath}_0 - \vec{k}_0).$

Esfera rodando sin deslizar en un recipiente cilíndrico, F1GIA 2016-17

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Análisis de la información cinemática en el enunciado

2.2 Reducciones cinemáticas

2.2.1 Movimiento {01}

2.2.2 Movimiento {21}

2.2.3 Movimiento {20}

2.3 Pivotamiento y rodadura

2.4 Cálculo de diferencias de aceleraciones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES