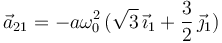Escuadra con barra vertical, Enero 2015 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

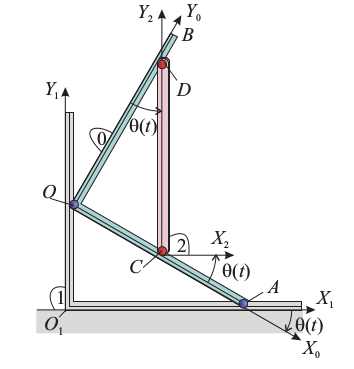
En la figura se muestran los sólidos rígidos "0" y "2" que realizan sendos movimientos planos respecto del plano director fijo 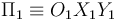$\Pi_1\equiv O_1X_1Y_1$ (sólido "1"). El sólido "0" está formado por dos barras, $O A$ y $O B$ , ambas de longitud $a$ y rígidamente unidas formado un recto. El sólido "2" es una barra rígida $C D$ , también de longitud $a$ , cuyos extremos siempre están en contacto con las barras $O A$ y $O B$ , respectivamente.

A partir de la posición inicial en que el vértice $O$ del sólido "0" coincide con el punto fijo $O 1$ , y las barras $O A$ y $O B$ están alineadas con los ejes $O 1 X 1$ y $O 1 Y 1$ , respectivamente, el sólido "0" se mueve, respecto de $Π 1$ , rotando en sentido horario. En dicho movimiento, el módulo del correspondiente vector rotación tiene un valor constante en el tiempo $ω 0$ . Además, los puntos $O$ y $A$ de dicho sólido recorren, respectivamente, los ejes $O 1 Y 1$ y $O 1 Y 1$ . Simultáneamente, los extremos $C$ y $D$ del sólido "2" recorren las barras $O A$ y $O B$ ,respectivamente, de manera que $C D$ permanece en todo momento paralela al eje $O 1 Y 1$ .

Obtenga de manera razonada e indique la posición de los C.I.R. de los movimientos relativos {01}, {20} y {21} en el instante reflejado en la figura, en que el ́angulo $θ(t)$ tiene un valor $π / 6$ . Indique también las direcciones de las velocidades de los extremos $C$ y $D$ del sólido "2", medidas desde el sistema de referencia "1" (movimiento {21}).
Obtenga las reducciones cinemáticas de los tres movimientos en el instante mostrado en la figura.
También para la posición analizada en los apartados anteriores, determine la aceleración instantánea de los puntos del sólido "2" en el movimiento {21}.

2 Solución

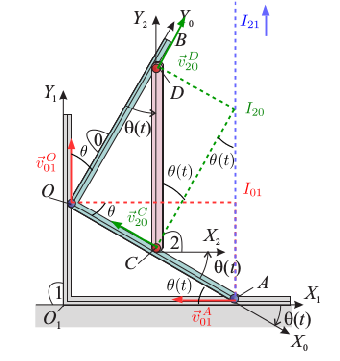
2.1 Posiciones de los CIR

La figura de la derecha muestra las posiciones de los CIR de los tres movimientos. La velocidad 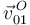$\vec{v}^{\,O}_{01}$ es paralela al eje $O Y 1$ , mientras que la velocidad 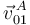$\vec{v}^{\,A}_{01}$ es paralela al eje $O X 1$ . Trazando las perpendiculares respectivas a los puntos $O$ y $A$ obtenemos la posición del CIR $I 01$ . Teniendo en cuenta que la longitud de la barra $O A$ es $a$ , la posición de $I 01$ es

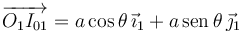
$\overrightarrow{O_1I_{01}} = a\cos\theta\,\vec{\imath}_1 + a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Con respecto al movimiento {20} el mismo procedimiento se aplica en los puntos $C$ y $D$ . Dado que la longitud de la barra $C D$ es $a$ , tenemos

$\overline{DI}_{20} = \overline{OC} = a\,\mathrm{sen}\,\theta, \qquad \overline{CI}_{20}=\overline{OB}=a\cos\theta$

Por tanto, la posición de $I 20$ usando la base del sólido "0" es

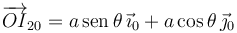
$\overrightarrow{OI}_{20} = a\,\mathrm{sen}\,\theta\,\vec{\imath}_0 + a\cos\theta\,\vec{\jmath}_0$

Podemos expresar la posición de $I 20$ en la base del sólido "1". Tenemos

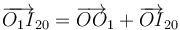
$\overrightarrow{O_1I}_{20} = \overrightarrow{OO}_{1} + \overrightarrow{OI}_{20}$

Del dibujo tenemos

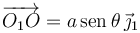
$\overrightarrow{O_1O} = a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

Y los vectores de la base del sólido "0" se pueden expresar en términos de los vectores de la base del sólido "1" como

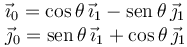
$\begin{array}{l} \vec{\imath}_0 = \cos\theta\,\vec{\imath}_1 - \mathrm{sen}\,\theta\,\vec{\jmath}_1 \\ \vec{\jmath}_0 = \mathrm{sen}\,\theta\,\vec{\imath}_1 + \cos\theta\,\vec{\jmath}_1 \end{array}$

Obtenemos al final

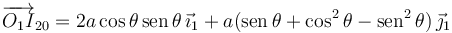
$\overrightarrow{O_1I}_{20} = 2a\cos\theta\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + a(\mathrm{sen}\,\theta + \cos^2\theta - \mathrm{sen}^2\,\theta)\,\vec{\jmath}_1$

Respecto al movimiento {21} el enunciado nos dice que la barra $C D$ se mantiene siempre paralela al eje $O 1 Y 1$ , es decir, realiza una traslación. Entonces el CIR debe estar en el infinito. Por otro lado, el teorema de los tres centros nos dice que $I 21$ debe estar alineado con $I 20$ y $I 01$ . La figura indica la dirección en la que se encuentra $I 21$ .

2.2 Reducciones cinemáticas

2.2.1 Movimiento {01}

Es un movimiento plano, entonces

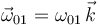
$\vec{\omega}_{01} = \omega_{01}\,\vec{k}$

Necesitamos la velocidad de dos puntos para determinar $ω 01$ . Determinamos los vectores de posición absolutos de los puntos $O$ y $A$ .

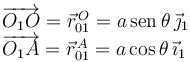
$\begin{array}{l} \overrightarrow{O_1O} = \vec{r}^{\,O}_{01} = a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 \\ \overrightarrow{O_1A} = \vec{r}^{\,A}_{01} = a\cos\theta\,\vec{\imath}_1 \end{array}$

Estos vectores dan la posición de estos puntos en todo instante. Podemos derivarlos respecto al tiempo para obtener las dos velocidades

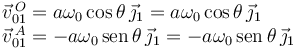
$\begin{array}{l} \vec{v}^{\,O}_{01} = a\omega_0\cos\theta\,\vec{\jmath}_1 = a\omega_0\cos\theta\,\vec{\jmath}_1 \\ \vec{v}^{\,A}_{01} = -a\omega_0\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 = -a\omega_0\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 \end{array}$

Usamos el teorema de Chasles para relacionar las dos velocidades.

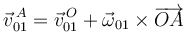
$\vec{v}^{\,A}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OA}$

El vector geométrico es

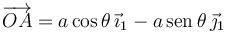
$\overrightarrow{OA} = a\cos\theta\,\vec{\imath}_1 - a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1$

y entonces

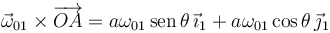
$\vec{\omega}_{01}\times\overrightarrow{OA} = a\omega_{01}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + a\omega_{01}\cos\theta\,\vec{\jmath}_1$

Por tanto

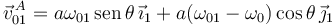
$\vec{v}^{\,A}_{01} = a\omega_{01}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + a(\omega_{01}-\omega_0)\cos\theta\,\vec{\jmath}_1$

Comparando con la expresión anterior de 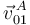$\vec{v}^{\,A}_{01}$ llegamos a

$ω 01 = - ω 0$

Y una posible reducción del movimiento {01} es

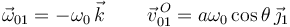
$\vec{\omega}_{01} = -\omega_0\,\vec{k}\,\qquad \vec{v}^{\,O}_{01} = a\omega_0\cos\theta\,\vec{\jmath}_1$

En el instante mostrado en la figura tenemos $θ = π / 6$ . La reducción cinemática es

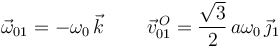
$\vec{\omega}_{01} = -\omega_0\,\vec{k}\,\qquad \vec{v}^{\,O}_{01} = \dfrac{\sqrt{3}}{2}\,a\omega_0\,\vec{\jmath}_1$

2.2.2 Movimiento {20}

Hemos visto que el movimiento {21} es una traslación, es decir, 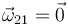$\vec{\omega}_{21}=\vec{0}$ . Podemos usar la composición {21} = {20} + {01} para obtener $\vec{\omega}_{20}$ . Tenemos

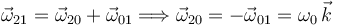
$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} \Longrightarrow \vec{\omega}_{20} = -\vec{\omega}_{01} = \omega_0\,\vec{k}$

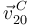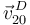Conocemos las direcciones de $\vec{v}^{\,C}_{20}$ y $\vec{v}^{\,D}_{20}$ . Del dibujo tenemos

$\vec{v}^{\,C}_{20} = v^C_{20}\,\vec{\imath}_0, \qquad \vec{v}^{\,D}_{20} = v^D_{20}\,\vec{\jmath}_0$

Usamos el teorema de Chasles para relacionar las dos velocidades

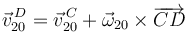
$\vec{v}^{\,D}_{20} = \vec{v}^{\,C}_{20} + \vec{\omega}_{20}\times\overrightarrow{CD}$

Hacemos el producto vectorial

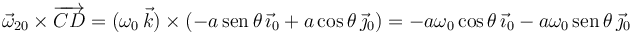
$\vec{\omega}_{20}\times\overrightarrow{CD} = (\omega_0\,\vec{k})\times(-a\,\mathrm{sen}\,\theta\,\vec{\imath}_0 + a\cos\theta\,\vec{\jmath}_0)= -a\omega_0\cos\theta\,\vec{\imath}_0 - a\omega_0\,\mathrm{sen}\,\theta\,\vec{\jmath}_0$

Tenemos entonces

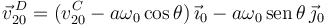
$\vec{v}^{\,D}_{20} = (v^C_{20} -a\omega_0\cos\theta)\,\vec{\imath}_0 - a\omega_0\,\mathrm{sen}\,\theta\,\vec{\jmath}_0$

Comparando con la expresión anterior de 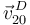$\vec{v}^{\,D}_{20}$ vemos que

$\vec{v}^C_{20} = a\omega_0\cos\theta\,\vec{\imath}_0, \qquad \vec{v}^D_{20} = -a\omega_0\,\mathrm{sen}\,\theta\,\vec{\jmath}_0$

Una posible reducción en el instante en que $θ = π / 6$ es

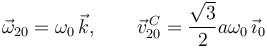
$\vec{\omega}_{20} = \omega_0\,\vec{k},\qquad \vec{v}^{\,C}_{20} = \dfrac{\sqrt{3}}{2}a\omega_0\,\vec{\imath}_0$

2.2.2.1 Resolución alternativa del movimiento {20}

Otra forma de calcular la reducción cinemática del movimiento {20} es encontrar el vector de posición de dos puntos del sólido "2" vistos desde el sólido "0", expresados en la base del sólido "0", y derivarlos respecto de tiempo. De la figura vemos que

$\overrightarrow{OC} = \vec{r}^{\,C}_{20} = a\,\mathrm{sen}\,\theta\,\vec{\imath}_0 \,\qquad \overrightarrow{OD} = \vec{r}^{\,D}_{20} = a\cos\theta\,\vec{\jmath}_0$

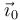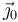Estas dos expresiones son válidas siempre. Al derivar respecto del tiempo respecto al sólido "0", los vectores $\vec{\imath}_0$ y $\vec{\jmath}_0$ son constantes, por lo que

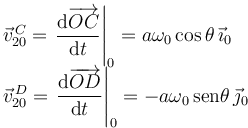
$\begin{array}{l} \vec{v}^{\,C}_{20} = \left.\dfrac{\mathrm{d}\overrightarrow{OC}}{\mathrm{d}t}\right|_0 = a\omega_0\cos\theta\,\vec{\imath}_0 \\ \vec{v}^{\,D}_{20} = \left.\dfrac{\mathrm{d}\overrightarrow{OD}}{\mathrm{d}t}\right|_0 = -a\omega_0\,\mathrm{sen}\theta\,\vec{\jmath}_0 \end{array}$

Relacionando las dos velocidades con el teorema de Chasles obtenemos $\vec{\omega}_{20}$ .

2.2.3 Movimiento {21}

Ya hemos visto que el movimiento {21} es una traslación, es decir

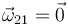
$\vec{\omega}_{21} = \vec{0}$

Necesitamos la velocidad en un punto. Podemos calcular la velocidad en $C$ usando la composición

${21} = {20} + {01}$

Tenemos

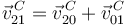
$\vec{v}^{\,C}_{21} = \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01}$

Hemos calculado ya el primer sumando. Para el segundo usamos la ecuación del campo de velocidades del movimiento {01}

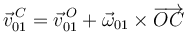
$\vec{v}^{\,C}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OC}$

El producto vectorial es

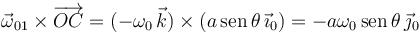
$\vec{\omega}_{01}\times\overrightarrow{OC} = (-\omega_0\,\vec{k})\times(a\,\mathrm{sen}\,\theta\,\vec{\imath}_0) = -a\omega_0\,\mathrm{sen}\,\theta\,\vec{\jmath}_0$

La velocidad buscada es

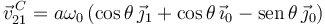
$\vec{v}^{\,C}_{21} = a\omega_0\,(\cos\theta\,\vec{\jmath}_1 + \cos\theta\,\vec{\imath}_0 - \mathrm{sen}\,\theta\,\vec{\jmath}_0)$

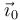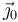Es conveniente usar sólo vectores de una base. Usando las expresiones de $\vec{\imath}_0$ y $\vec{\jmath}_0$ que hemos obtenido antes llegamos a

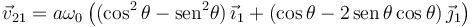
$\vec{v}_{21} = a\omega_0\left( (\cos^2\theta - \mathrm{sen}^2\theta)\,\vec{\imath}_1 + (\cos\theta - 2\,\mathrm{sen}\,\theta\cos\theta)\,\vec{\jmath}_1\right)$

No hay letra en la velocidad porque en una traslación todos los puntos tienen la misma velocidad. La reducción cinemática cuando $θ = π / 6$ es

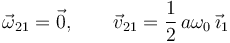
$\vec{\omega}_{21} = \vec{0}, \qquad \vec{v}_{21} = \dfrac{1}{2}\,a\omega_0\,\vec{\imath}_1$

En este instante la velocidad es paralela al eje $O 1 X 1$ . Esto es consistente con el hecho de que $I 21$ este en el infinito en la dirección del eje $O 1 Y 1$ .

2.2.3.1 Resolución alternativa de {21}

El movimiento {21} también puede describirse encontrando el vector de posición de un punto de la barra $C D$ expresado en la base "1" y derivarlo respecto del tiempo. Por ejemplo

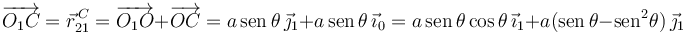
$\overrightarrow{O_1C} = \vec{r}^{\,C}_{21} = \overrightarrow{O_1O} + \overrightarrow{OC} = a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 + a\,\mathrm{sen}\,\theta\,\vec{\imath}_0 = a\,\mathrm{sen}\,\theta\cos\theta\,\vec{\imath}_1 + a(\mathrm{sen}\,\theta - \mathrm{sen}^2\theta)\,\vec{\jmath}_1$

Derivando esta expresión respecto del tiempo obtenemos 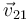$\vec{v}_{21}$ . Hemos usado la expresión de 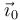$\vec{\imath}_0$ en función de la base del sólido "1" del primer apartado.

2.3 Aceleración del movimiento {21}

Necesitamos la velocidad de algún punto de modo que su expresión sea valida en todo instante. Podemos usar la que hemos calculado en el apartado anterior

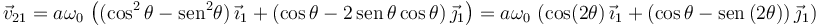
$\vec{v}_{21} = a\omega_0\,\left( (\cos^2\theta - \mathrm{sen}^2\theta)\,\vec{\imath}_1 + (\cos\theta - 2\,\mathrm{sen}\,\theta\cos\theta)\,\vec{\jmath}_1\right) = a\omega_0\,\left(\cos(2\theta)\,\vec{\imath}_1 + (\cos\theta - \mathrm{sen}\,(2\theta))\,\vec{\jmath}_1\right)$

Derivando respecto al tiempo obtenemos la aceleración

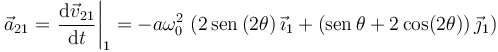
$\vec{a}_{21} = \left.\dfrac{\mathrm{d}\vec{v}_{21}}{\mathrm{d}t}\right|_1 = -a\omega_0^2\, \left( 2\,\mathrm{sen}\,(2\theta)\,\vec{\imath}_1 + (\mathrm{sen}\,\theta + 2\cos(2\theta))\,\vec{\jmath}_1 \right)$

Cuando $θ = π / 6$ resulta

$\vec{a}_{21} = -a\omega^2_0\,(\sqrt{3}\,\vec{\imath}_1 + \dfrac{3}{2}\,\vec{\jmath}_1)$

Escuadra con barra vertical, Enero 2015 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posiciones de los CIR

2.2 Reducciones cinemáticas

2.2.1 Movimiento {01}

2.2.2 Movimiento {20}

2.2.2.1 Resolución alternativa del movimiento {20}

2.2.3 Movimiento {21}

2.2.3.1 Resolución alternativa de {21}

2.3 Aceleración del movimiento {21}

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES