Electrostática en presencia de dieléctricos (GIOI)

De Laplace

1 Concepto de dieléctrico

Los medios materiales responden de diferentes maneras en presencia de un campo eléctrico aplicado. Un material conductor es aquel que permite el movimiento de cargas por su interior, llegando finalmente al estado de equilibrio electrostático.

Los dieléctricos o aislantes son aquellos materiales que no permiten el movimiento de cargas por su interior. En ellos todas las cargas están ligadas en sus respectivos átomos y no pueden desplazarse. Suelen ser materiales plásticos o cristalinos con fuertes enlaces covalentes. Incluso en materiales dieléctricos el campo no es el mismo que en el vacío, por la presencia de dipolos inducidos por el campo eléctrico. El límite es el modelo de dieléctrico ideal o aislante perfecto, que no permite en absoluto el movimiento de cargas por su interior.

El efecto de una conductividad finita en un dieléctrico real se analiza al estudiar las corrientes eléctricas. Aquí consideramos el modelo más simple de un dieléctrico ideal.

Podemos preguntarnos, si un dieléctrico ideal no permite el movimiento de cargas y éstas no pueden redistribuirse por el material, ¿cómo influye en el campo eléctrico? ¿Por qué no es equivalente al vacío?

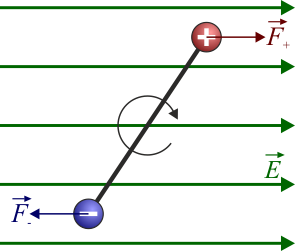
La respuesta es que aunque un dieléctrico ideal no tenga cargas libres, sí tiene dipolos. Un dipolo eléctrico consiste en un par de cargas de la misma magnitud y signo opuesto separadas una cierta distancia. Un dipolo produce un campo eléctrico característico.

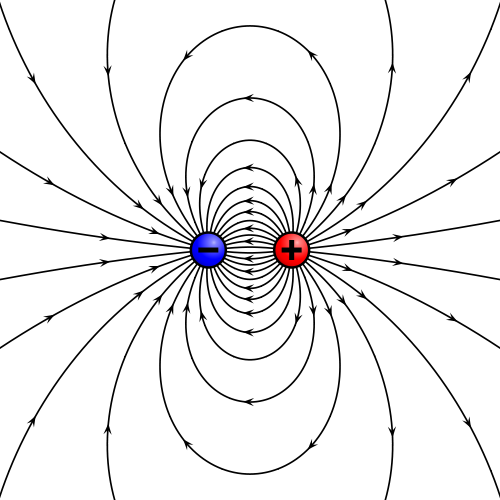
En un dipolo las cargas no son libres, sino que están ligadas entre sí, pero sus campos no se neutralizan por estar separadas. Un dieléctrico ideal está constituido por millones de dipolos elementales, que afectan al campo eléctrico.

¿De dónde proceden estos dipolos? Hay de dos tipos, no excluyentes:

Dipolos inducidos

Son los que aparecen por la aplicación de un campo eléctrico. Consideremos, por ejemplo, un átomo de helio, formado por un núcleo de carga positiva rodeado de una nube de carga negativa. En ausencia de campo externo el núcleo se encuentra en el centro de la nube negativa y no hay separación de los centros de carga.

        

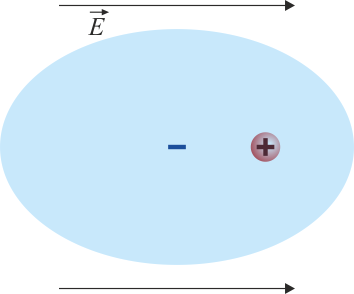
Si se aplica un campo externo, el núcleo es empujado en el sentido del campo, mientras que la nube es empujada en el sentido opuesto. El resultado es una separación de los centros de carga, formándose un dipolo. Nótese que las cargas son ligadas y en ningún momento llega a arrancarse un electrón del átomo.

Dipolos permanentes

Las llamadas sustancias polares, como el agua, están formadas por moléculas que ya de por sí son dipolos.

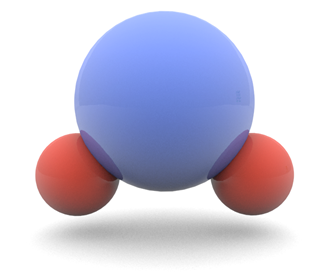
En una molécula de agua, el oxígeno tira de los electrones con más fuerza que los átomos de hidrógeno, de forma que en la molécula aparece una densidad de carga negativa en la parte donde se encuentra el oxígeno y positiva en el lado opuesto. La molécula se comporta como un dipolo.

Esto no ocurre en todas las sustancias. El dióxido de carbono, por ejemplo, es una sustancia apolar, aunque el oxígeno tira más de los electrones que el carbono, la simetría de la molécula evita que se produzca separación de los centros de carga.

El efecto de un campo aplicado sobre un dipolo permanente es orientarlo. Al tirar de la carga positiva en un sentido y de la negativa en otro, el resultado es un par de fuerzas que tiende a alinear el dipolo con el campo aplicado.

2 Efecto de un dieléctrico entre conductores

Tanto si los dipolos son inducidos como si son permanentes, el efecto de un campo aplicado es que aparezca una distribución de dipolos alineados con el campo aplicado.

Supongamos que tenemos un condensador plano cuyas placas tienen cargas 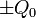y entre las cuales hay vacío. En este caso aparece un campo eléctrico entre las placas que va de la placa positiva a la negativa y cuyo valor es

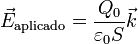
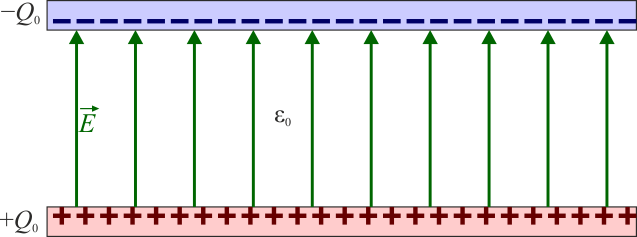
Si ahora colocamos un dieléctrico entre las placas, este material se polariza, y los dipolos del material se alinean con el campo aplicado.

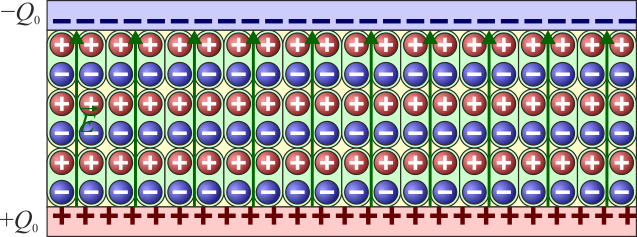
Ahora bien, los dipolos tienen cargas positivas junto a las negativas de sus vecinos, por lo que sus efectos se cancelan, salvo los situados en los límites del dieléctrico

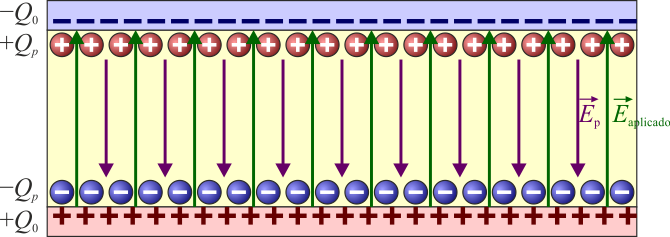
El efecto de los dipolos del dieléctrico es equivalente entonces a una densidad de carga (conocida como carga de polarización o carga ligada) situada en la frontera del dieléctrico o en los puntos donde la polarización no es uniforme. Esta carga de polarización produce su propio campo, que va en sentido opuesto al campo aplicado, pero tiene menor intensidad

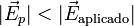
de forma que el resultado neto es una reducción del campo total

La polarización del dieléctrico es proporcional al campo aplicado, por lo que el campo total es proporcional a la carga de las placas y se puede escribir

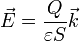
donde es una propiedad del dieléctrico conocida como su permitividad absoluta. Puesto que el campo eléctrico es menor que el que habría con el condensador en vacío debe ser

Para medir las propiedades de un dieléctrico se usa tanto la permitividad absoluta como la permitividad relativa, definida como el cociente

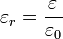
(a la permitividad relativa también se la denota como K). Tanto a la permitividad absoluta como a la relativa se la suele denominar simplemente permitividad, ya que el contexto permite distinguirlas fácilmente:

• La permitividad absoluta es una cantidad con unidades (se mide en F/m en el SI) cuyo valor es muy pequeño en las unidades fundamentales del SI. Así, para el agua, la permitividad absoluta vale

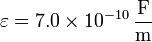
• La permitividad relativa es una magnitud adimensional (un número) que es siempre mayor que la unidad y cuyo valor suele ser moderado. Así, para el agua su permitividad relativa es

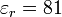
y para otras sustancias como el metacrilato o plexiglás vale aproximadamente 3.

3 Condensadores con dieléctricos

El efecto de introducir un dieléctrico en un condensador con una carga fijada es el de reducir el campo entre las placas. Esto implica que disminuye la diferencia de potencial entre ellas. Si la distancia entre placas es a

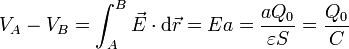
donde la nueva capacidad del condensador es

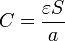
es decir, basta con sustituir la permitividad del vacío por la del dieléctrico.

Puesto que la permitividad de un dieléctrico es mayor que la del vacío, el resultado de rellenar un dieléctrico es aumentar su capacidad, es decir:

• A igualdad de carga, la d.d.p. es menor en el condensador con dieléctrico, como acabamos de ver.
• A igualdad de d.d.p., el condensador con dieléctrico almacena más carga en sus placas.

Este resultado se extiende a la energía almacenada en el condensador, que pasa a ser

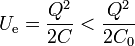
siendo C₀ la capacidad en vacío, es decir, que a igualdad de carga, la energía almacenada en un condensador con dieléctrico es menor que la que hay en vacío. Si tenemos un condensador cargado e intercalamos entre sus placas una lámina de dieléctrico, se produce una disipación de energía. A nivel microscópico esto ocurre porque la polarización de un dieléctrico implica fricción y producción de calor.

Por contra, si lo que se fija es la d.d.p.

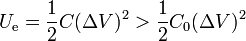
la energía del condensador es mayor con dieléctrico que sin él.

Para este segundo caso, podemos imaginar un proceso en el que tenemos un condensador en vacío, que almacena una cierta energía. Si manteniendo la d.d.p. introducimos entre sus placas una lámina de dieléctrico, la energía almacenada aumenta.

¿De donde sale esta energía extra? De la fuente de tensión que mantiene constante el voltaje. Para ello debe introducir una cantidad extra de carga (ya que la capacidad aumenta). Para ello, realiza un trabajo igual a la carga que coloca multiplicada por la diferencia de potencial a la que la eleva

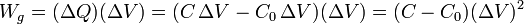
Es decir, la fuente realiza un trabajo igual al doble del aumento en la energía interna. Esto quiere decir que en realidad estamos disipando energía, ya que la fuente realiza un trabajo mayor que lo que se almacena, por lo que se produce una disipación en forma de calor.

4 Conductores con dieléctricos

Lo anterior se generaliza a un problema general en el que tengamos un sistema de conductores entre los cuales hay dieléctricos. En este caso tenemos un problema del potencial, análogo al caso de los conductores en el vacío, pero con diferentes dieléctricos entre ellos. Estos dieléctricos no tienen por qué ser homogéneos ya que la permitividad puede variar de un punto a otro.

Este problema general del potencial casi en ningún caso posee solución analítica y se requiere el uso de ordenadores.

En algunos casos el sistema puede modelarse por elementos más sencillos. Así, un sistema con dos capas de dieléctrico equivale a dos condensadores en serie

        

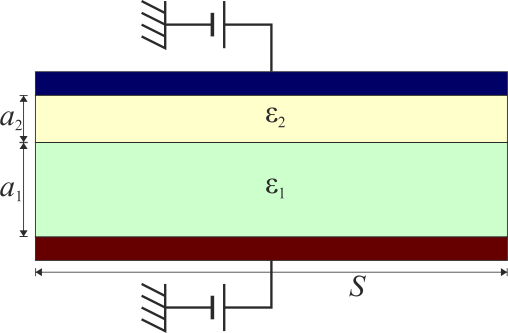
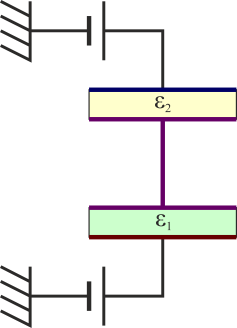
y uno con dos bloques adyacentes puede modelarse como dos condensadores en paralelo

        

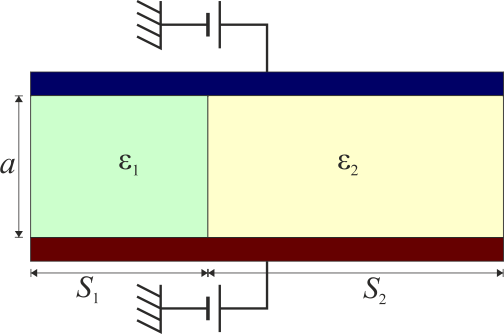
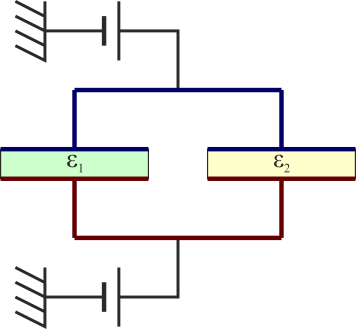
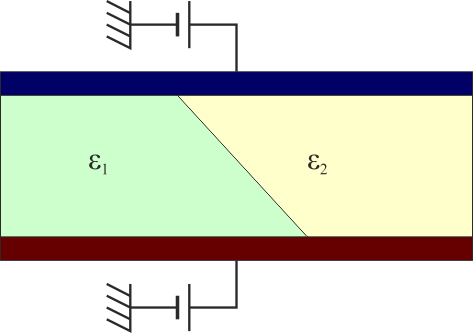
pero uno en el que la interfaz (la frontera entre los medios) no sea ni paralela ni perpendicular a las placas equivale a un solo condensador, pero no se puede modelar por un sistema sencillo, sino que hay que calcular numéricamente su capacidad

        

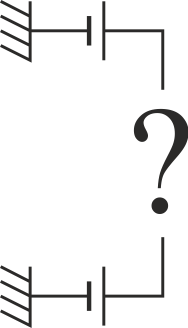
En un sistema general de conductores con dieléctricos, sigue siendo cierto que la energía del sistema es

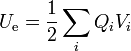
y que esta energía puede hallarse a partir del campo eléctrico mediante la integral extendida a todo el espacio

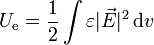
donde la permitividad será la del vacío donde no haya dieléctrico y la del dieléctrico donde sí lo haya.

5 Ruptura de un dieléctrico

Antes se ha dicho que la capacidad de un condensador aumenta al colocar un dieléctrico entre sus placas. Podría pensarse que esta es la razón de que los condensadores se fabriquen siempre con un dieléctrico entre las armaduras. No obstante, no es esta la razón principal.

• En primer lugar, proporcionan rigidez mecánica. Si se coloca un dieléctrico entre las placas, éstas no se pueden tocar, por lo que no es más difícil que se produzca un cortocircuito. Con dos placas en vacío, teniendo en cuenta lo poco separadas que están, cualquier vibración haría que se rozaran.
• Son más fáciles de montar. Puesto que ya no es necesario que las placas conductoras sean rígidas, éstas pueden reducirse a una película de pintura conductora o a una fina lámina de metal adherida al dieléctrico.
• Son más resistentes a la ruptura dieléctrica. Cuando entre dos puntos de un dieléctrico o en el aire se establece un campo eléctrico muy intenso, este puede llegar a ionizar el medio y saltar una chispa. Cuando esto ocurre, se dice que el dieléctrico se ha perforado, el condensador se quema y queda inservible. En términos circuitales, es como si hubiéramos hecho un cortocircuito entre las placas. El campo mínimo para que esto ocurra se denomina campo de ruptura o rigidez dieléctrica del material

• En el caso del aire, el valor del campo de ruptura es muy variable, pero es del orden de 3 MV/m.
• En el caso del papel con cera que se usa en condensadores, el campo de ruptura asciende a entre 40 y 60 MV/m

Esto quiere decir que la carga máxima que se puede meter en un condensador con papel de cera es como unas 50 veces la que almacenaría un condensador equivalente en vacío (teniendo en cuenta que 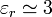) y además soporta una d.d.p. 20 veces mayor.