Ejercicio de dinámica de la partícula, Febrero 2013 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Acción del cable sobre la partícula
- 2.2 Potencia del motor y trabajo que realiza

1 Enunciado

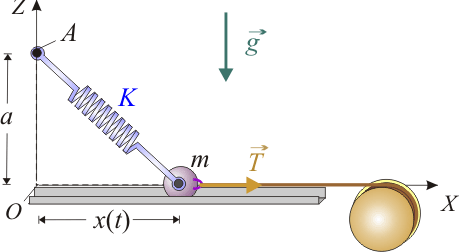
Una pieza de masa m está obligada a moverse siempre dentro de un carril fijo horizontal, perpendicular a la dirección de la gravedad,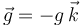 $\vec{g} =-g\!\ \vec{k}$ . Un resorte de longitud natural despreciable y constante recuperadora

K

conecta la pieza con un punto fijo

A

, situado a una altura

a

en la vertical del extremo

O

del carril. El sistema se diseña de manera que los parámetros anteriores verifiquen la relación,

K a = m g

. En el otro extremo del carril hay un motor que enrolla de manera continua un cable conectado a la pieza, haciendo que ésta se desplace con velocidad constante de valor

v 0

, desde su posición inicial en el extremo

O

del carril. El contacto entre la pieza y el carril es de naturaleza rugosa, estando caracterizado por un coeficiente de rozamiento dinámico de valor

μ

.

Obtenga la expresión de la fuerza que describe la acción del cable sobre la pieza, en función de su distancia al extremo O.
Determine la potencia instantánea desarrollada por el motor en un instante $t$ , medido desde el instante inicial. Calcule también el trabajo realizado por el motor.

2 Solución

2.1 Acción del cable sobre la partícula

El cable conectado al motor y a la partícula obliga a ésta a moverse con velocidad constante a lo largo del carril, que tomaremos como dirección $O X$ en el sistema de referencia cartesiano utilizado para describir analíticamente las magnitudes vectoriales. Se tendrá, por tanto:

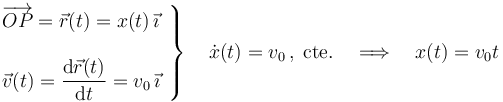
$\left.\begin{array}{l}\displaystyle\overrightarrow{OP}=\vec{r}(t)=x(t)\!\ \vec{\imath}\\ \\ \displaystyle\vec{v}(t)=\frac{\mathrm{d}\vec{r}(t)}{\mathrm{d}t}=v_0\!\ \vec{\imath}\end{array}\right\}\quad \dot{x}(t)=v_0\,\mathrm{,}\,\;\mathrm{cte.}\quad\Longrightarrow\quad x(t)=v_0 t$

pues la partícula parte del punto $O$ , donde hemos situado el origen del sistema de referencia. La acción del cable sobre la partícula se modela mediante una fuerza colineal con el cable y que, en general, será de la forma...

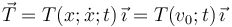
$\vec{T}=T(x;\dot{x};t)\!\ \vec{\imath}=T(v_0;t)\!\ \vec{\imath}$

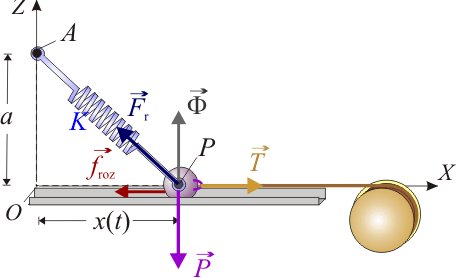
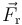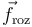Pero además, sobre la partícula actúan la gravedad, el resorte y el vínculo rugoso constituido por el carril con rozamiento. Estas acciones están modeladas o descritas, respectivamente, por la fuerza peso $\vec{P}$ , la fuerza recuperadora $\vec{F}_\mathrm{r}$ , la fuerza de reacción vincular (lisa) $\vec{\Phi}$ , y la fuerza de rozamiento $\vec{f}_\mathrm{roz}$ . Las propiedades de estas fuerzas permiten describirlas analíticamente, como sigue:

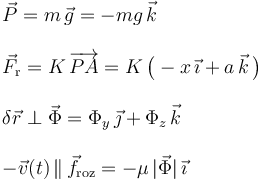
$\begin{array}{l}\displaystyle\vec{P}=m\!\ \vec{g}=-mg\!\ \vec{k}\\ \\ \displaystyle\vec{F}_\mathrm{r}=K\!\ \overrightarrow{PA}=K\!\ \big(-x\!\ \vec{\imath}+a\!\ \vec{k}\!\ \big)\\ \\ \delta\vec{r}\perp\vec{\Phi}=\Phi_y\!\ \vec{\jmath}+\Phi_z\!\ \vec{k}\\ \\ -\vec{v}(t)\!\ \|\!\ \vec{f}_\mathrm{roz}=-\mu\!\ |\vec{\Phi}|\!\ \vec{\imath}\end{array}$

Obsérvese que la partícula se mueve con velocidad constante. Por tanto, el fenómeno de rozamiento es dinámico. Asumiendo que son aplicables las leyes del rozamiento seco, se tendrá que la correspondiente fuerza es en todo momento proporcional al módulo de la fuerza de reacción del vínculo liso o geométrico, siendo la constante de proporcionalidad el coeficiente de rozamiento dinámico $μ$ .

Aplicando las leyes de la Dinámica al cuerpo puntual $P$ , y teniendo en cuenta que éste se mueve con velocidad constante en módulo, dirección y sentido, se obtiene el siguiente conjunto de ecuaciones:

$\vec{T}+\vec{P}+\vec{F}_\mathrm{r}+\vec{\Phi}+\vec{f}_\mathrm{roz}=m\ \frac{\mathrm{d}\vec{v}(t)}{\mathrm{d}t}=\vec{0}\quad\Longrightarrow\quad\left\{\begin{array}{l}T[x(t)]-K\!\ x(t)-\mu\!\ |\vec{\Phi}|=0\\ \\ \displaystyle \Phi_y=0\\ \\ \displaystyle -mg+Ka+\Phi_z=0\end{array}\right.$

... que, una vez resuelto, proporciona la expresión de cómo debe ser la fuerza o tensión realizada por el cable. Nótese que, en el caso particular que se plantea en este ejericio, en que los parámetros del sistema son tales que $K a = m g$ , la componente vertical de la fuerza recuperadora del resorte cancela con la fuerza peso, de manera que dicha componente de la fuerza vincular asociada a la restricción geométrica va a ser nula. Y como tampoco hay otras fuerzas con componentes en la dirección del eje $O Y$ , se tiene que la fuerza vincular lisa va a ser nula y, en consecuencia, tampoco existirá fuerza de rozamiento. En conscuencia, la tensión del cable que modela la acción del motor sobre la partícula, sólo debe compensar a la componente horizontal de la fuerza recuperador del resorte:

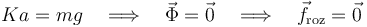
$Ka=mg\quad\Longrightarrow\quad\vec{\Phi}=\vec{0}\quad\Longrightarrow\quad\vec{f}_\mathrm{roz}=\vec{0}$ $\quad$ $\Rightarrow$ $\quad$ $\vec{T}=T[x(t)]\!\ \vec{\imath}=K\!\ x(t)\!\ \vec{\imath}$

2.2 Potencia del motor y trabajo que realiza

Asumiendo que el cable se limita a transmitir la acción del motor a la partícula, se tendrá que la potencia instantánea desarrollada por el motor será igual al trabajo que por unidad de tiempo realiza la fuerza $\vec{T}$ :

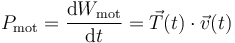
$P_\mathrm{mot}=\frac{\mathrm{d}W_\mathrm{mot}}{\mathrm{d}t}=\vec{T}(t)\cdot\vec{v}(t)$

Sustituyendo la expresiones de fuerza y velocidad de la partícula, se obtiene que para que ésta realice un movimiento uniforme, el motor debe desarrollar una potencia instantánea que crece linealmente con el tiempo, a partir del instante $t = 0$ en que empieza a arrastra a la partícula:

$P_\mathrm{mot}(t)=\frac{\mathrm{d}W_\mathrm{mot}}{\mathrm{d}t}=K\!\ v_0\!\ x(t)=K\!\ v_0^2\!\ t$

El trabajo realizado por el motor va a depender del tiempo y, en consecuencia, de la posición de la partícula: al cabo de un tiempo $t$ , en que la partícula ha recorrido una distancia $x$ , se tendrá...

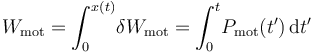
$W_\mathrm{mot}=\int_0^{x(t)}\! \delta W_\mathrm{mot}=\int_0^{t}\! P_\mathrm{mot}(t^\prime)\!\ \mathrm{d}t^\prime$ $\quad$ $\Rightarrow$ $W_\mathrm{mot}(t)=\frac{1}{2}\ K\!\ v_0^2\!\ t^2=\frac{1}{2}\ K\!\ x^2(t)$

Obsérvese que este resultado nos proporciona una pista clara acerca de en qué se emplea la energía suministrada por el motor al sistema: en un instante arbitrario $t$ , en que la partícula ha recorrido una distancia $x$ sobre el carril, la energía potencial asociada a la elongación del resorte es:

$U_\mathrm{r}[x(t)]=\frac{1}{2}\ K\!\ \big[x^2(t)+a^2\big]$

Si en el instante inicial la partícula se encuentra en el extremo $O$ del carril, la energía potencial inicial del resorte es:

$U_\mathrm{r}[x(t=0)]=\frac{1}{2}\ K\!\ a^2$

Por tanto, el trabajo realizado por el motor desde el momento inicial hasta el instante $t$ , coincide con la variación sufrida por la energía potencial del resorte en dicho intervalo de tiempo:

$W_\mathrm{mot}(t)=\frac{1}{2}\ K\!\ x^2(t)=U_\mathrm{r}[x(t)]-U_\mathrm{r}[x(t=0)]=\Delta U_\mathrm{r}$

Ejercicio de dinámica de la partícula, Febrero 2013 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Acción del cable sobre la partícula

2.2 Potencia del motor y trabajo que realiza

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES