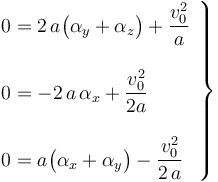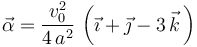Ejercicio de cinemática del sólido rígido, Febrero 2013 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

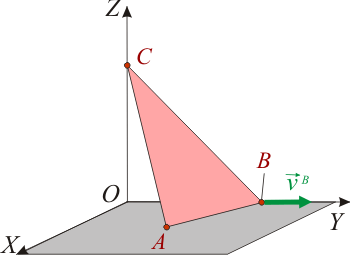
Una pieza triangular

A B C

se mueve respecto de un sistema de referencia

O X Y Z

, comportándose como un sólido rígido. Los vértices

C

y

B

de la pieza van recorriendo los ejes

O Z

y

O Y

, respecti-vamente, mientras que el vértice

A

se desplaza siempre contenido en el plano

O X Y

. En un determinado instante, cuando los vértices ocupan las posiciones de coordenadas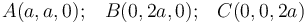 $A(a,a,0)\mathrm{;}\quad B(0,2a,0)\mathrm{;}\quad C(0,0,2a)$

la velocidad instantánea del vértice $B$ es 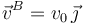$\vec{v}^B=v_0\!\ \vec{\jmath}$ . Determine, para dicho instante de tiempo:

Velocidad del vértice $A$ y vector rotación instantánea.
Eje instantáneo de rotación y mínimo deslizamiento.
Derivada instantánea del vector rotación, sabiendo que el vértice $B$ se mueve con velocidad instantánea constante.

2 Solución

2.1 Velocidad del vértice A y vector rotación

Para determinar la velocidad instantánea del vértice $A$ podemos utilizar las propiedades conocidas del movimiento de los tres vértices y la propiedad de equiproyectividad del campo de velocidades del sólido:

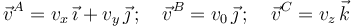
$\vec{v}^A=v_x\!\ \vec{\imath}+v_y\!\ \vec{\jmath}\,\mathrm{;}\,\quad\vec{v}^B=v_0\!\ \vec{\jmath}\,\mathrm{;}\,\quad\vec{v}^C=v_z\!\ \vec{k}$

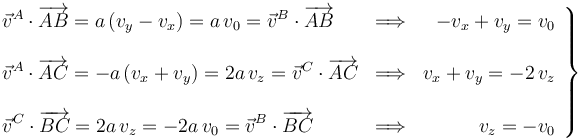
$\left.\begin{array}{lcr}\displaystyle\vec{v}^A\cdot \overrightarrow{AB}=a\!\ (v_y-v_x)=a\!\ v_0=\vec{v}^B\cdot \overrightarrow{AB}&\Longrightarrow & -v_x+v_y= v_0\\ \\ \displaystyle \vec{v}^A\cdot \overrightarrow{AC}=-a\!\ (v_x+v_y)=2a\!\ v_z=\vec{v}^C\cdot \overrightarrow{AC}&\Longrightarrow & v_x+v_y=-2\!\ v_z\\ \\ \displaystyle \vec{v}^C\cdot \overrightarrow{BC}=2a\!\ v_z=-2a\!\ v_0=\vec{v}^B\cdot \overrightarrow{BC}&\Longrightarrow & v_z=-v_0 \end{array}\right\}$ $\quad$ $\Rightarrow$ $\quad$ $\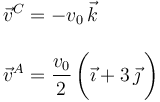begin{array}{l}\vec{v}^C=-v_0\!\ \vec{k}\\ \\ \displaystyle \vec{v}^A=\frac{v_0}{2}\!\ \bigg( \vec{\imath}+ 3\!\ \vec{\jmath}\!\ \bigg)\end{array}$

Para calcular las componentes cartesianas del vector rotación que caracteriza el movimiento del sólido en el instante considerado, podemos utilizar el teorema de Chasles:

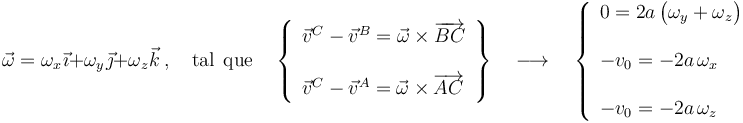
$\vec{\omega}=\omega_x\!\ \vec{\imath}+\omega_y\!\ \vec{\jmath}+\omega_z\!\ \vec{k}\,\mathrm{,}\,\quad\mathrm{tal}\;\,\mathrm{que}\quad\left\{ \begin{array}{l}\vec{v}^C-\vec{v}^B=\vec{\omega}\times\overrightarrow{BC}\\ \\ \vec{v}^C-\vec{v}^A=\vec{\omega}\times\overrightarrow{AC}\end{array}\right\} \quad\longrightarrow\quad\left\{\begin{array}{l}\displaystyle 0=2a\!\ \big( \omega_y+\omega_z \big)\\ \\ \displaystyle -v_0=-2a\!\ \omega_x \\ \\ \displaystyle -v_0=-2a\!\ \omega_z\end{array}\right.$

Resolviendo este sistema algebraico se obtiene:

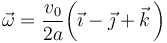
$\vec{\omega}=\frac{v_0}{2a}\bigg(\vec{\imath}-\vec{\jmath}+\vec{k}\!\ \bigg)$

2.2 Eje instantáneo de rotación y mínimo deslizamiento

En el instante bajo estudio, el invariante escalar del campo de velocidades es no nulo, por tanto, el movimiento instantáneo del sólido es un movimiento helicoidal tangente. Es decir, en dicho instante, el sólido rígido ejecuta una rotación instantánea alrededor de un eje, a la vez que todos los puntos del sólido realizan una traslación instantánea paralela a dicho eje. Es éste el eje instantáneo de rotación y mínimo desplazamiento, $Δ EIRMD$ , cuya ecuación vectorial es:

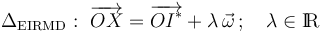
$\Delta_\mathrm{EIRMD}:\ \overrightarrow{OX}=\overrightarrow{OI^*}+\lambda\!\ \vec{\omega}\,\mathrm{;}\,\quad\lambda\in \mathrm{I}\!\mathrm{R}$

La posición del punto $I *$ del EIRMD, está completamente determinada por los elementos de la reducción cinemática. Así, si se toma como centro de reducción el punto $B$ , se tendrá:

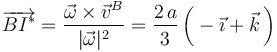
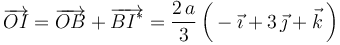
$\overrightarrow{BI^*}=\frac{\vec{\omega}\times\vec{v}^B}{|\vec{\omega}|^2}=\frac{2\!\ a}{3}\!\ \bigg(-\vec{\imath}+ \vec{k}\!\ \bigg)$ $\Rightarrow$ $\overrightarrow{OI}=\overrightarrow{OB}+\overrightarrow{BI^*}=\frac{2\!\ a}{3}\!\ \bigg(-\vec{\imath}+ 3\!\ \vec{\jmath}+ \vec{k}\!\ \bigg)$

La velocidad instantánea de cualquier punto $P$ de sólido rígido puede escribirse como la suma de dos términos vectoriales que se corresponden con la composición de los movimientos de traslación y rotación anteriormente descritos:

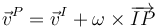
$\vec{v}^P=\vec{v}^I+\omega\times \overrightarrow{IP}$

En los puntos del sólido rígido (reales o virtuales) que se encuentran sobre el EIRMD, la velocidad sólo tiene la componente de traslación 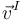$\vec{v}^I$ , paralela a dicho eje y al vector rotación instantánea. Además, éstos son los puntos del campo de velocidades en que dicha magnitud tiene módulo mínimo:

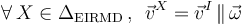
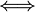
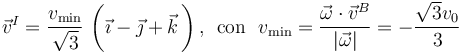
$\forall\, X\in \Delta_\mathrm{EIRMD}\,\mathrm{,}\,\;\,\vec{v}^X=\vec{v}^I\!\ \|\!\ \vec{\omega}$ $\Longleftrightarrow$ $\vec{v}^I=\frac{v_\mathrm{min}}{\sqrt{3}}\ \bigg(\vec{\imath}-\vec{\jmath}+\vec{k}\!\ \bigg)\,\mathrm{,}\,\;\,\mathrm{con}\,\;\, v_\mathrm{min}=\frac{\vec{\omega}\cdot \vec{v}^B}{|\vec{\omega}|}=-\frac{\sqrt{3}v_0}{3}$

2.3 Derivada instantánea del vector rotación

Para determinar las componentes de esta magnitud instantánea vectorial,

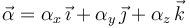
$\vec{\alpha}=\alpha_x\!\ \vec{\imath}+\alpha_y\!\ \vec{\jmath}+\alpha_z\!\ \vec{k}$

podemos aplicar las propiedades del campo de aceleración del sólido rígido, del cual sabemos lo siguiente: el vértice $B$ se mueve con velocidad constante y, por tanto, su aceleración es nula; el vértice $C$ puede estar acelerado, pero sólo tiene componente en la dirección del unitario $\vec{k}$ , y la aceleración del vértice $A$ no puede tener componente en la dirección de $\vec{k}$ ; es decir...

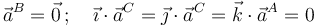
$\vec{a}^B=\vec{0}\,\mathrm{;}\,\quad\vec{\imath}\cdot\vec{a}^C=\vec{\jmath}\cdot\vec{a}^C=\vec{k}\cdot\vec{a}^A=0$

Combinando estas propiedades con las expresiones vectoriales que determinan el campo de aceleraciones instantánteas, a partir de la aceleración de un punto, el vector rotación y su derivada instantánea,

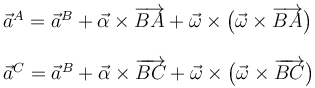
$\begin{array}{l}\vec{a}^A=\vec{a}^B+\vec{\alpha}\times\overrightarrow{BA}+\vec{\omega}\times\big(\vec{\omega}\times\overrightarrow{BA}\big)\\ \\ \vec{a}^C=\vec{a}^B+\vec{\alpha}\times\overrightarrow{BC}+\vec{\omega}\times\big(\vec{\omega}\times\overrightarrow{BC}\big)\end{array}$

... obtenemos un conjunto de ecuaciones que permiten determinar las componentes cartesianas de la derivada del vector rotación:

$\left.\begin{array}{l}\displaystyle 0=2\!\ a \big(\alpha_y+\alpha_z\big)+\frac{v_0^2}{a}\\ \\ \displaystyle 0=-2\!\ a \!\ \alpha_x+\frac{v_0^2}{2a}\\ \\ \displaystyle 0= a \big(\alpha_x+\alpha_y\big)-\frac{v_0^2}{2\!\ a}\end{array}\right\}$ $\Rightarrow$ $\vec{\alpha}=\frac{v_0^2}{4\!\ a^2}\ \bigg( \vec{\imath}+ \vec{\jmath}-3\! \ \vec{k}\!\ \bigg)$

Ejercicio de cinemática del sólido rígido, Febrero 2013 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Velocidad del vértice A y vector rotación

2.2 Eje instantáneo de rotación y mínimo deslizamiento

2.3 Derivada instantánea del vector rotación

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES