Ejercicio de Mecánica del Punto Material, Diciembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

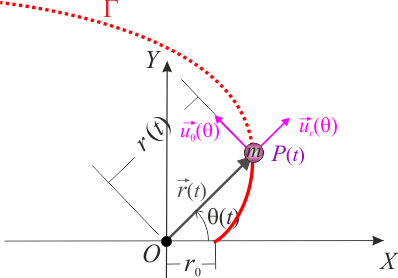
Una partícula $P$ de masa $m$ se mueve en el plano $O X Y$ describiendo una trayectoria espiral $Γ$ , cuya ecuación en coordenadas polares ${r,θ}$ es:

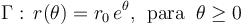
$\Gamma:\!\ r(\theta)=r_0\!\ e^\theta\mathrm{,}\;\;\mathrm{para}\;\;\theta\geq 0$

de manera que $r (t)$ es la distancia medida desde el origen $O$ del sistema de referencia, a la posición $P (t)$ que ocupa la partícula en un cierto instante, y $θ(t)$ el ángulo (medido en radianes) que en dicho instante forma el radio vector 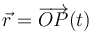$\vec{r}=\overrightarrow{OP}(t)$ con el eje OX. Además, el movimiento de la partícula es tal que su momento cinético respecto de O es un vector constante de módulo conocido, $L 0$ .

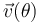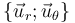Obtenga la expresión $\vec{v}(\theta)$ del vector velocidad instantánea de la partícula $P$ como una función de la posición, dada por el ángulo $θ$ . Se sugiere utilizar la base de las coordenadas polares, $\{\vec{u}_r\mathrm{;}\, \vec{u}_\theta\}$ .
Obtenga la expresión del vector aceleración instantánea de la partícula en función de su posición, 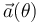$\vec{a}(\theta)$ . ¿Qué propiedades tienen la dirección, el sentido y el módulo de la fuerza resultante que actúa sobre la partícula?
Obtenga las componentes intrínsecas de la velocidad (módulo) y de la aceleración. Determine las direcciones tangente y normal a la trayectoria (en términos de las base de las coordenadas polares), así como el radio de curvatura de la trayectoria en cada punto.
Sabiendo que en el instante $t = 0$ la partícula se encuentra a una distancia $r 0$ del punto $O$ , calcule su energía cinética inicial ¿Se conservará durante el movimiento? Obtenga la ley horaria $θ(t)$ que describe cómo se mueve la partícula.

2 Solución

Como se recordará, la posición de un punto en el plano cartesiano $O X Y$ , puede determinarse también utilizando las coordenas polares, $P (r,θ)$ , siendo $r$ la distancia del punto $P$ al origen $O$ del sistema de referencia, y $θ$ , el ángulo formado por el segmento $\overrightarrow{OP}$ con el eje cartesiano $O X$ . De esta forma, se tendrá:

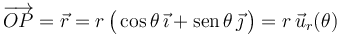
$\overrightarrow{OP}=\vec{r}=r\!\ \big(\cos\theta\!\ \vec{\imath}+\mathrm{sen}\!\ \theta\!\ \vec{\jmath}\!\ \big)=r\!\ \vec{u}_r(\theta)$

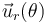donde $\vec{u}_r(\theta)$ , es un vector unitario con la dirección y el siempre del segmento orientado $\overrightarrow{OP}$ .

Si se utiliza este sistema de coordenadas para describir el movimiento en un plano de una partícula material $P$ , las correspondientes ecuaciones horarias 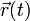$\vec{r}(t)$ estarán determinadas por las leyes horarias 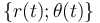$\{r(t)\mathrm{;}\!\ \theta(t)\}$ , que describen cómo cambian durante el movimiento la distancia de la partícula al punto fijo $O$ , y el ángulo que el radiovector posición forma con la dirección fija tomado como eje $O X$ .

La derivada con respecto al tiempo de las ecuaciones horarias, proporciona el vector velocidad instantánea expresado como una función del tiempo, que en términos de las coordenadas polares será de la forma:

$\vec{v}(t)=\frac{\mathrm{d}\vec{r}(t)}{\mathrm{d}t}=\dot{\vec{r}}(t)=\dot{r}(t)\!\ \big[\cos\theta(t)\!\ \vec{\imath}+\mathrm{sen}\!\ \theta(t)\!\ \vec{\jmath}\!\ \big]\!\ +\ r(t)\dot{\theta}(t)\!\ \big[-\mathrm{sen}\!\ \theta(t)\!\ \vec{\imath}+\cos \theta(t)\!\ \vec{\jmath}\!\ \big]$

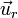En esta expresió aparece un segundo vector unitario, definido en términos del valor del parámetro $θ$ , que tiene la dirección del plano que es perpendicular a la del segmento orientado $\overrightarrow{OP}$ y, por tanto, a la del vector unitario $\vec{u}_r$ :

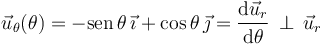
$\vec{u}_\theta(\theta)=-\mathrm{sen}\!\ \theta\!\ \vec{\imath}+\cos\theta\!\ \vec{\jmath}=\frac{\mathrm{d}\vec{u}_r}{\mathrm{d}\theta}\!\ \perp \!\ \vec{u}_r$

Utilizando los vectores ortonormales 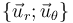$\{\vec{u}_r\mathrm{;}\!\ \vec{u}_\theta\}$ como base para describir magnitudes vectoriales en el plano $O X Y$ , se tendrá que la expresión en coordenadas polares de la velocidad instantánea de una partícula que se mueve en dicho plano, será:

$\vec{v}(t)=\dot{r}(t)\!\ \vec{u}_r[\theta(t)]\!\ + \!\ r(t)\dot{\theta}(t)\!\ \vec{u}_\theta[\theta(t)]$

Obsérvese que de esta expresión se deduce que el vector 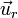$\vec{u}_r$ indica el sentido en que se mueve la partícula $P$ cuando ésta aumenta su distancia $r$ al punto $O$ , manteniéndose constante el valor del ángulo $θ$ . 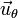Análogamente, si la partícula realiza un movimiento instantáneo manteniendo la distancia $r$ constante, y aumentando el valor del $θ$ , se desplaza en la dirección y el sentido indicados por $\vec{u}_\theta$ .

Si derivamos de nuevo con respecto al tiempo en la anterior expresión horaria para la velocidad instantánea, obtenemos la correspondiente expresión en coordenadas polares del vector aceleración instantánea de una partícula que se mueve contenida en un plano:

$\vec{a}(t)=\frac{\mathrm{d}\vec{v}(t)}{\mathrm{d}t}=\big[\ddot{r}(t)-r(t)\dot{\theta}^2(t)\big]\!\ \vec{u}_r[\theta(t)]\!\ + \big[2\dot{r}(t)\dot{\theta}(t)+\!\ r(t)\ddot{\theta}(t)\big]\!\ \vec{u}_\theta[\theta(t)]=a_r(t)\!\ \vec{u}_r(t)+a_\theta(t)\!\ \vec{u}_\theta(t)$

Estas expresiones generales para la velocidad y la aceleración instantáneas de toda partícula con movimiento en el plano, las aplicaremos a continuación al caso particular de una que describe la trayectoria espiral $Γ$ definida en el enunciado.

2.1 Velocidad instantánea como función de la posición

Una vez conocida la trayectoria seguida por la partícula, las leyes horarias $r (t)$ y $θ(t)$ correspondientes a su movimiento quedan unívocamente relacionadas:

$\forall\, t\;\;P\in\Gamma:\!\ r(\theta)=r_0\!\ e^\theta\quad\Longrightarrow\quad r(t)=r_0\!\ e^{\theta(t)}$

Consecuentemente, las derivadas con respecto al tiempo de ambas leyes también están relacionadas:

$\frac{\mathrm{d}r(t)}{\mathrm{d}t}=r_0\!\ e^{\theta(t)}\!\ \frac{\mathrm{d}\theta(t)}{\mathrm{d}t}\quad\Longrightarrow\quad \dot{r}(t)=r_0\!\ e^{\theta(t)}\!\ \dot{\theta} (t)=r(t)\!\ \dot{\theta} (t)$

Sustituyendo estos resultados en la expresión del vector velocidad instantánea, se obtiene:

$\vec{v}(t)=r(t)\!\ \dot{\theta} (t)\!\ \bigg\{\vec{u}_r[\theta(t)]\!\ + \!\ \vec{u}_\theta[\theta(t)]\bigg\}$

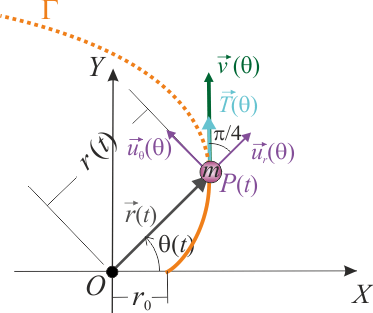
De esta expresión ya podemos determinar la dirección tangente a la trayectoria en cada punto, en función del valor del parámetro $θ$ :

$\vec{T}(\theta)=\frac{\vec{v}}{|\vec{v}|}=\frac{1}{\sqrt{2}}\big[\vec{u}_r(\theta)\!\ + \!\ \vec{u}_\theta(\theta)\big]$

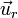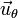Es decir, en todas las posiciones de la partícula a lo largo de la trayectoria, la dirección tangente a ésta y, por tanto, la dirección del vector velocidad, forma sendos ángulos $π / 4$ con las direcciones $\vec{u}_r$ y $\vec{u}_\theta$ .

Sin embargo, se solicita la expresión del vector velocidad en función de la posición, dada por un valor del ángulo $θ$ . Por tanto, necesitamos conocer información sobre la ley horaria verificada por dicho parámetro durante el movimiento, de manera que podamos determinar cómo es la derivada temporal $\dot{\theta}$ como una función de la posición. Es decir, además de conocer la trayectoria seguida por la partícula, necesitamos información sobre cómo recorre dicha trayectoria. Y esta se proporciona en el enuncidado al indicar que el momento cinético de la partícula respecto del origen $O$ permanece constante durante el movimiento. Si su módulo tiene un valor conocido $L 0$ , se cumplirá que:

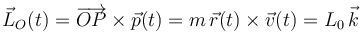
$\vec{L}_O(t)=\overrightarrow{OP}\times\vec{p}(t)=m\!\ \vec{r}(t)\times\vec{v}(t)=L_0\!\ \vec{k}$

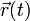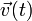Obsérvese que al moverse la partícula en el plano $O X Y$ , los vectores $\vec{r}(t)$ y $\vec{v}(t)$ se encuentran siempre contenidos en dicho plano, por lo que su producto vectorial será, en todo momento, perpendicular a $O X Y$ . Es decir, el momento cinético de la partícula respecto del punto $O$ también va a tener dirección constante: la del vector unitario $\vec{k}$ de las componentes cartesianas. Sustituyendo en la expresión anterior los valores en cada instante de los vectores posición y velocidad, se obtiene:

$\vec{L}_O(t)=m\!\ \vec{r}(t)\times\vec{v}(t)=m r^2(t)\dot{\theta}(t)\!\ \vec{k}\quad\Longrightarrow\quad\dot{\theta}(t)=\frac{L_0}{m\!\ r^2(t)}=\frac{L_0}{m\!\ r_0^2}\ e^{-2\theta(t)}=\dot{\theta}[\theta(t)]$

Este expresión permite determinar el valor instantáneo de $\dot{\theta}$ en función de la posición que la partícula ocupa en cada instante, la cuál viene dada por el valor del parámetro $θ$ . Y puesto que éste también determina el del parámetro $r$ a través de la ecuación de la trayectoria, podemos obtener la expresión del vector velocidad instantánea como en términos $θ$ , es decir, como una función de la posición de la partícula

$\vec{v}(\theta)=r(\theta)\!\ \dot{\theta} (\theta)\!\ \bigg[\vec{u}_r(\theta)\!\ + \!\ \vec{u}_\theta(\theta)\bigg]=\frac{L_0}{m\!\ r_0}\!\ e^{-\theta}\!\ \bigg[\vec{u}_r(\theta)\!\ + \!\ \vec{u}_\theta(\theta)\bigg]$

2.2 Aceleración instantánea como función de la posición

Al comienzo de la solución del ejercicio se recordaba la expresión en coordenadas polares de la aceleración instantánea de una partícula que realiza un movimiento plano. Sus componentes $a r$ y $a θ$ se definen en términos de las coordenadas polares y de sus derivadas temporales de primer y segundo orden. Los datos suministrados en el enunciaco a cerca de la trayectoria de la partícula, y los resultados obtenidos en el apartado anterior para las leyes horarias de los parámetros $r$ y $θ$ , son suficientes para determinar dichas componentes mediante cálculo directo. Sin embargo, en este ejercicio podemos reducir la labor de cálculo utilizando el hecho de que el movimiento de la partícula es tal que su momento cinético respecto del punto $O$ permanece constante en el tiempo. Es decir, si 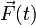$\vec{F}(t)$ es la resultante de la fuerza que en cada instante ésta aplicada sobre la partícula, está deber ser tal que se verifique:

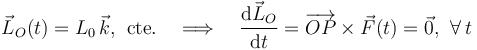
$\vec{L}_O(t)=L_0\!\ \vec{k}\mathrm{,}\;\;\mathrm{cte.}\quad\Longrightarrow\quad\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\overrightarrow{OP}\times\vec{F}(t)=\vec{0}\mathrm{,}\;\;\forall\, t$

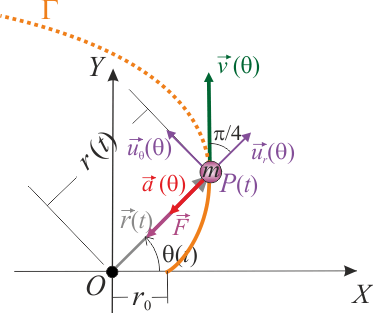
En principio, son posibles dos situaciones: que la fuerza sea nula en todo instante, o que siempre sea colineal con el segmento orientado $\overrightarrow{OP}$ . Obsérvese que el primer supuesto no es compatible con la propiedades del sistema: si la fuerza neta que actúa sobre la partícula es siempre nula, ésta se debe encontrar en reposo o realizando un movimiento rectilíneo uniforme. Pero, como hemos visto en el apartado anterior, el vector tangente a la trayectoria depende del ángulo $θ$ y éste cambia durante el movimiento, pues 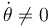$\dot{\theta}\neq 0$ . Por tanto, dicho vector no tiene dirección constante, por lo que la trayectoria de la partícula no es una recta. En consecuencia, la fuerza neta que actúa sobre la partícula es siempre colineal con el segmento que pasa por el origen del sistema y por la propia partícula y, por tanto, sólo tendrá componente en la dirección del vector 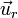$\vec{u}_r$ . Y si aplicamos la segunda ley de Newton, se obtiene que la aceleración sólo tendrán dicha componente:

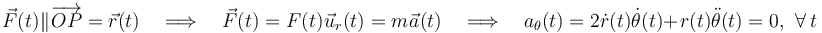
$\vec{F}(t)\!\ \| \!\ \overrightarrow{OP}=\vec{r}(t)\quad\Longrightarrow\quad\vec{F}(t)=F(t)\!\ \vec{u}_r(t)=m\!\ \vec{a}(t)\quad\Longrightarrow\quad a_\theta(t)=2\dot{r}(t)\dot{\theta}(t)+\!\ r(t)\ddot{\theta}(t)=0\mathrm{,}\;\;\forall\, t$

Luego, sólo hemos de calcular los dos términos de la componente radial de la aceleración:

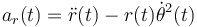
$a_r(t)=\ddot{r}(t)-r(t)\dot{\theta}^2(t)$

Utilizando los resultados del apartado anterior, podemos obtener fácilmente la expresión del segundo término en función de la posición:

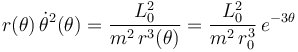
$r(\theta)\!\ \dot{\theta}^2(\theta)=\frac{L_0^2}{m^2\!\ r^3(\theta)}=\frac{L_0^2}{m^2\!\ r_0^3}\!\ e^{-3\theta}$

Para calcular el primer término tenemos en cuenta que, en el caso bajo estudio de trayectoria espiral recorrida de manera que el momento cinético respecto de $O$ sea constante, se cumple:

$\dot{r}(t)=r(t)\!\ \dot{\theta}(t)=\frac{L_0}{m\!\ r(t)}\quad\Longrightarrow\quad\ddot{r}(t)=\frac{\mathrm{d}\dot{r}(t)}{\mathrm{d}t}=-\frac{L_0}{m\!\ r^2(t)}\!\ \dot{r}(t)=-\frac{L_0^2}{m^2\!\ r^3(t)}\quad\Longrightarrow\quad\ddot{r}(\theta)=-\frac{L_0^2}{m^2\!\ r^3(\theta)}$

Es decir, en cada instante los términos de la componente radial de la aceleración (única componente), son opuestos:

$\vec{a}(\theta)=\bigg[\ddot{r}(\theta)-r(\theta)\!\ \dot{\theta}^2 (\theta) \bigg]\!\ \vec{u}_r(\theta)=-\frac{2L_0^2}{m^2\!\ r_0^3}\!\ e^{-3\theta}\!\ \vec{u}_r(\theta)=-\frac{2L_0^2}{m^2\!\ r^3(\theta)}\!\ \vec{u}_r(\theta)$

En cuanto a las caraterísticas de la fuerza aplicada...

$\vec{F}(t)=m\!\ \vec{a}[\theta(t)]=-\frac{2L_0^2}{m^2\!\ r^3(t)}\!\ \vec{u}_r[\theta(t)]\ \|\ -\vec{u}_r(\theta)\mathrm{,}\;\;\forall\,t$

Por tanto, se trata de una fuerza central con centro en el origen $O$ , al que apunta en todo instante, y cuya intensidad es inversamente proporcional al cubo de la distancia que separa a la partícula del centro del movimimiento.

2.3 Componentes intrínsecas de las magnitudes cinemáticas

2.3.1 Vectores del triedro intrínseco

Con los resultados obtenidos en los apartados anteriores, ya podemos determinar cómo van a ser los vectores del triedro intrínseco en cada posición de la partícula sobre la trayectoria. En el apartado 2.1 obtuvimos la expresión en polares del vector unitario tangente, teniendo en cuenta que la velocidad instantánea es siempre colineal con la dirección tangente a la trayectoria en cada punto, y considerando que el sentido de dicho vector es el del movimiento de la partícula sobre la trayectoria: $\vec{T}(\theta)=\frac{\vec{v}(\theta)}{|\vec{v}(\theta)|}=\frac{1}{\sqrt{2}}\bigg[\vec{u}_r(\theta)\!\ + \!\ \vec{u}_\theta(\theta)\bigg]$

El vector binormal podemos determinarlo a partir de los vectores velocidad y aceleración:

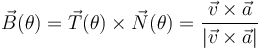
$\vec{B}(\theta)=\vec{T}(\theta)\times\vec{N}(\theta)=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}$

Utilizando las expresiones obtenidas en los apartados anteriores para estos vectores, se obtiene:

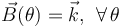
$\vec{v}(\theta)\times\vec{a}(\theta)=-\frac{2L_0^3}{m^3\!\ r^4(\theta)}\!\ \bigg[\vec{u}_r(\theta)+\vec{u}_\theta(\theta)\bigg]\times\vec{u}_r(\theta)=-\frac{2L_0^3}{m^3\!\ r^4(\theta)}\!\ \vec{k}$ $\quad$ $\Rightarrow$ $\quad$ $\vec{B}(\theta)=\vec{k}\mathrm{,}\;\;\forall\,\theta$

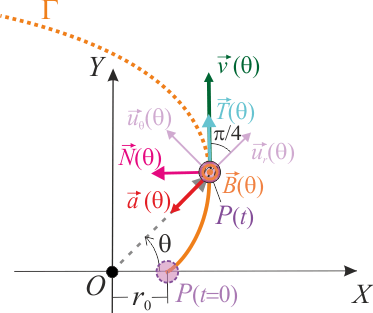
Y el vector normal a la trayectoria en cada punto, expresado en coordenadas polares, será:

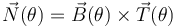
$\vec{N}(\theta)=\vec{B}(\theta)\times\vec{T}(\theta)$ $\quad$ $\Rightarrow$ $\quad$ $\vec{N}(\theta)=\frac{1}{\sqrt{2}}\!\ \vec{k}\times\bigg[\vec{u}_r(\theta) + \vec{u}_\theta(\theta)\bigg]=\frac{1}{\sqrt{2}}\!\ \bigg[-\vec{u}_r(\theta) + \vec{u}_\theta(\theta)\bigg]$

2.3.2 Componentes intrínsecas de velocidad y aceleración

Al definir el vector tangente de manera que su sentido sentido coincida con el del vector velocidad, la celerdidad $v (θ)$ o componente intrínseca, coincide con el módulo de dicho vector:

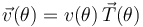
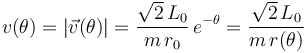
$\vec{v}(\theta)=v(\theta)\!\ \vec{T}(\theta)$ $\quad$ $\Rightarrow$ $\quad$ $v(\theta)=|\vec{v}(\theta)|=\frac{\sqrt{2}\!\ L_0}{m\!\ r_0}\!\ e^{-\theta}= \frac{\sqrt{2}\!\ L_0}{m\!\ r(\theta)}$

Y puesto que tenemos las expresiones en polares de los vectores del triedro intrínseco en cada punto, así como del vector aceleración, no tenemos más que proyectar éste en las direcciones de $\vec{T}$ y $\vec{N}$ para obtener las respectivas componentes tangencial y normal de la aceleración de la partícula:

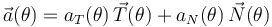
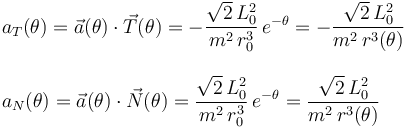
$\vec{a}(\theta)=a_T(\theta)\!\ \vec{T}(\theta)+a_N(\theta)\!\ \vec{N}(\theta)$ $\quad$ $\Rightarrow$ $\quad$ $\begin{array}{l}\displaystyle a_T(\theta)=\vec{a}(\theta)\cdot\vec{T}(\theta)=-\frac{\sqrt{2}\!\ L_0^2}{m^2\!\ r_0^3}\!\ e^{-\theta}=-\frac{\sqrt{2}\!\ L_0^2}{m^2\!\ r^3(\theta)}\\ \\ \displaystyle a_N(\theta)=\vec{a}(\theta)\cdot\vec{N}(\theta)=\frac{\sqrt{2}\!\ L_0^2}{m^2\!\ r_0^3}\!\ e^{-\theta}=\frac{\sqrt{2}\!\ L_0^2}{m^2\!\ r^3(\theta)}\end{array}$ $\quad$ $\Rightarrow$ $\quad$ $\forall\,t\mathrm{,}\;\;\left\{\begin{array}{l}v[\theta(t)]>0\\ \\ \displaystyle\frac{\mathrm{d}v(t)}{\mathrm{d}t}=a_T[\theta(t)]<0\end{array}\right.$

Obsérvese que mientras que la celeridad de la partícula es siempre positiva, su derivada temporal (es decir, la componente tangencial de la aceleración) tiene un valor negativo en todo instante, lo que significa que el movimiento de la partícula es decelerado o frenado.

2.3.3 Radio de curvatura de la trayectoria

Para calcular el valor de esta propiedad de la trayectoria en cada uno de sus puntos, aplicamos la relación que guarda con la componente normal de la aceleración de una partícula $P$ que recorra dicha trayectoria:

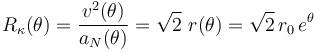
$a_N(t)=\frac{v^2(t)}{R_\kappa[P(t)]}$ $\quad$ $\Rightarrow$ $\quad$ $R_\kappa(\theta)=\frac{v^2(\theta)}{a_N(\theta)}=\sqrt{2}\ r(\theta)=\sqrt{2}\!\ r_0\!\ e^\theta$

2.4 Energía cinética inicial y ley horaria

La energía cinética de la partícula $K (t)$ , se define en términos de la masa y la celeridad de la partícula. Y puesto que anteriormente hemos obtenido una expresión de esta magnitud en términos de la posición de la partícula, podemos determinar su energía cinética inicial si conocemos su posición en el instante considerado como $t = 0$ :

$\left.\begin{array}{l}\displaystyle K(t)=\frac{1}{2}\!\ m\!\ v^2[\theta(t)]=\frac{L_0^2}{m\!\ r^2(t)}\\ \\ r(t=0)=r_0\end{array}\right\}$ $\quad$ $\Rightarrow$ $\quad$ $K(t=0)=\frac{1}{2}\!\ m \!\ v^2[\theta(t)]=\frac{L_0^2}{m\!\ r^2_0}$

Para comprobar si esta magnitud cinética permanece constante en el tiempo no tenemos más que calcular su derivada temporal. Como consecuencia de la definición de energía cinética para una partícula de masa constante, dicha derivada es proporcional al producto de la celeridad por la componente tangencial de la aceleración. Y como en el caso bajo estudio ambas cantidades son no nulas, se tendrán que la energía cinética no permanece constante; es decir, no se conserva. Concretamente, dicha magnitud decrede durante el movimiento, ya que su derivada con respecto al tiempo va a ser menor que cero:

$\frac{\mathrm{d}K(t)}{\mathrm{d}t}=\frac{1}{2}\!\ m\!\ \frac{\mathrm{d}}{\mathrm{d}t}\bigg[v^2(t)\bigg]= m\!\ v(t)\!\ \frac{\mathrm{d}v(t)}{\mathrm{d}t}<0\mathrm{,}\;\;\forall\,t$

Si queremos conocer cómo evoluciona durante el movimiento la energía cinética, o cualquiera de las magnitudes cinemáticas para las que hemos obtenido expresiones en función de la posición de la partícula, hemos de determinar la ley horaria $θ(t)$ verificada por el parámetro utilizado para indicar la posición. Para ello, utilizamos la ecuación diferencial que se puede formular a partir de la expresión obtenida en el apartado 2.1 para la derivada instantánea del ángulo $θ$ : en un intervalo de tiempo infinitesimal $d t$ , dicho ángulo experimentará una variación $dθ$ , tal que:

$\mathrm{d}\theta=\dot{\theta}[\theta(t)]\!\ \mathrm{d}t=\frac{L_0}{m\!\ r_0^2}\ e^{-2\theta(t)}\!\ \mathrm{d}t$

Aplicando el método de separación de variables, que consiste en separar en cada miembro los factores que dependen de una misma variable ( $θ$ ó $t$ ), la anterior ecuación diferencial puede ser fácilmente integrada:

$\int\! e^{2\theta}\!\ \mathrm{d}\theta=\frac{L_0}{m\!\ r_0^2}\!\ \int\!\mathrm{d}t\quad\longrightarrow\quad \frac{1}{2}\!\ e^{2\theta}=\frac{L_0}{m\!\ r_0^2}\!\ t + C\mathrm{,}$

donde $C$ es una constante de integración que calcularemos exigiendo que se verifiquen las condiciones iniciales del problema: en el instante $t = 0$ la partícula se encuentra en un punto de la trayectoria $Γ$ , dado por una valor $θ 0 = θ(t = 0)$ tal que aquélla está a una distancia $r 0$ del origen $O$ :

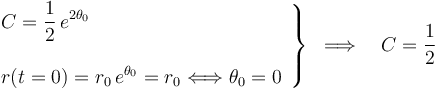
$\left.\begin{array}{l}\displaystyle C=\frac{1}{2}\!\ e^{2\theta_0}\\ \\ \displaystyle r(t=0)=r_0\!\ e^{\theta_0}=r_0\Longleftrightarrow \theta_0=0\end{array}\right\}\;\;\Longrightarrow\quad C=\frac{1}{2}$ $\quad$ $\Rightarrow$ $\quad$ $\theta(t)=\frac{1}{2}\!\ \ln\left[1+\frac{2\!\ L_0}{m\!\ r_0^2}\!\ t\right]$

La ley horaria $r (t)$ para la distancia de la partícula al origen del sistema de referencia se obtiene exigiendo que aquélla se mueva recorriendo la trayectoria $Γ$ :

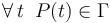
$\forall\, t\;\; P(t)\in\Gamma$ $\quad$ $\Rightarrow$ $\quad$ $r(t)=r_0\!\ e^{\theta(t)}=r_0\!\ \left[1+\frac{2\!\ L_0}{m\!\ r_0^2}\!\ t\right]^{1/2}$

Ejercicio de Mecánica del Punto Material, Diciembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Velocidad instantánea como función de la posición

2.2 Aceleración instantánea como función de la posición

2.3 Componentes intrínsecas de las magnitudes cinemáticas

2.3.1 Vectores del triedro intrínseco

2.3.2 Componentes intrínsecas de velocidad y aceleración

2.3.3 Radio de curvatura de la trayectoria

2.4 Energía cinética inicial y ley horaria

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES