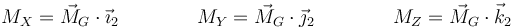Ecuaciones de Euler (CMR)

De Laplace

Contenido

1 Introducción
2 Deducción de las ecuaciones
3 Movimiento de un sólido libre
4 Movimiento de una peonza pesada

1 Introducción

En las ecuaciones para la dinámica de un sólido

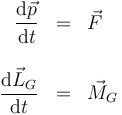
$\begin{array}{rcl}\dfrac{\mathrm{d}\vec{p}}{\mathrm{d}t}&=&\vec{F} \\ && \\ \dfrac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}&=&\vec{M}_G\end{array}$

la cantidad de movimiento y el momento cinético posee expresiones análogas; una mide la traslación y el otro la rotación

$\vec{p}=M\vec{v}_G\qquad\qquad \vec{L}_G = \overline{\overline{I}}\cdot\vec{\omega}$

pero con una diferencia fundamental: mientras la masa es una constante de movimiento, el tensor de inercia no lo es.

Uno podría pensar que, dado que el sólido es rígido, su tensor de inercia no se ve afectado por el movimiento, pero no es así, ya que depende de las posiciones de cada partícula.

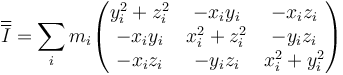
$\overline{\overline{I}}=\sum_i m_i\begin{pmatrix}y_i^2+z_i^2 & -x_iy_i & -x_i z_i \\ -x_iy_i & x_i^2+z_i^2 & -y_iz_i \\ -x_iz_i & -y_iz_i & x_i^2+y_i^2\end{pmatrix}$

Cuando las partículas se mueven, los valores de las coordenadas cambian y el tensor de inercia depende del tiempo, por lo que debe ser incluido a la hora de derivar.

El problema “se resuelve” si empleamos un sistema de referencia ligado al sólido. En este sistema de ejes el sólido está inmóvil y por tanto el tensor de inercia es constante. El problema es que es ahora el propio sistema de referencia el que depende del tiempo y por tanto debe ser incluido en los cálculos. Cuando hacemos esto, obtenemos las denominadas ecuaciones de Euler.

2 Deducción de las ecuaciones

Suponemos, como en otras ocasiones, dos sistemas de referencia. Uno fijo (“sistema 1”) y uno ligado al sólido (“sistema 2”). Para distinguir las componentes en ambos sistemas, usaremos minúsculas para el sistema 1 y mayúsculas para el 2.

Elegimos el sistema 2 de manera que sus ejes apunten en las direcciones de los ejes principales del sólido (que siempre existen y son ortogonales entre sí). De esta forma, el tensor de inercia no solo es constante, sino que es diagonal

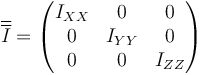
$\overline{\overline{I}}=\begin{pmatrix}I_{XX} & 0 & 0 \\ 0 & I_{YY} & 0 \\ 0 & 0 & I_{ZZ}\end{pmatrix}$

En esta base, la velocidad angular y el momento cinético respecto al CM se escriben

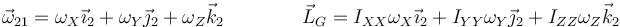
$\vec{\omega}_{21} = \omega_X \vec{\imath}_2 +\omega_Y \vec{\jmath}_2+\omega_Z\vec{k}_2 \qquad\qquad \vec{L}_G = I_{XX}\omega_X \vec{\imath}_2 +I_{YY}\omega_Y \vec{\jmath}_2+I_{ZZ}\omega_Z\vec{k}_2$

las ecuaciones de la dinámica del sólido están expresadas suponiendo un sistema de referencia fijo, por lo que para derivar aquí respecto al tiempo debemos aplicar la fórmula de Poisson

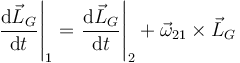
$\left.\frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}\right|_2+\vec{\omega}_{21}\times\vec{L}_G$

siendo

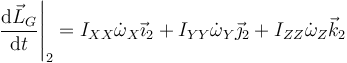
$\left.\frac{\mathrm{d}\vec{L}_G}{\mathrm{d}t}\right|_2=I_{XX}\dot{\omega}_X \vec{\imath}_2 +I_{YY}\dot{\omega}_Y \vec{\jmath}_2+I_{ZZ}\dot{\omega}_Z\vec{k}_2$

y

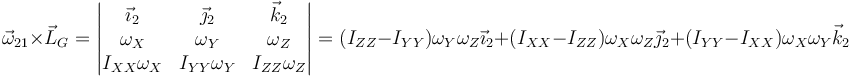
$\vec{\omega}_{21}\times\vec{L}_G=\left|\begin{matrix} \vec{\imath}_2 & \vec{\jmath}_2 & \vec{k}_2 \\ \omega_X & \omega_Y & \omega_Z \\ I_{XX}\omega_X & I_{YY}\omega_Y & I_{ZZ}\omega_Z\end{matrix}\right|= (I_{ZZ}-I_{YY})\omega_Y\omega_Z \vec{\imath}_2 + (I_{XX}-I_{ZZ})\omega_X\omega_Z \vec{\jmath}_2 + (I_{YY}-I_{XX})\omega_X\omega_Y\vec{k}_2$

Si sustituimos e igualamos al momento de las fuerzas obtenemos el sistema de ecuaciones de Euler

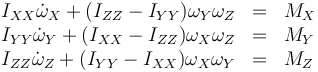
$\begin{array}{rcl}I_{XX}\dot{\omega}_X+ (I_{ZZ}-I_{YY})\omega_Y\omega_Z & = & M_X \\ I_{YY}\dot{\omega}_Y+ (I_{XX}-I_{ZZ})\omega_X\omega_Z & = & M_Y \\ I_{ZZ}\dot{\omega}_Z+ (I_{YY}-I_{XX})\omega_X\omega_Y & = & M_Z\end{array}$

aquí, $M X$ representa la componente del momento resultante respecto a la base móvil, es decir

$M_X=\vec{M}_G\cdot\vec{\imath}_2\qquad\qquad M_Y=\vec{M}_G\cdot\vec{\jmath}_2\qquad\qquad M_Z=\vec{M}_G\cdot\vec{k}_2$

3 Movimiento de un sólido libre

4 Movimiento de una peonza pesada

Ecuaciones de Euler (CMR)

De Laplace

Contenido

1 Introducción

2 Deducción de las ecuaciones

3 Movimiento de un sólido libre

4 Movimiento de una peonza pesada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES